- 2024-01-26 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
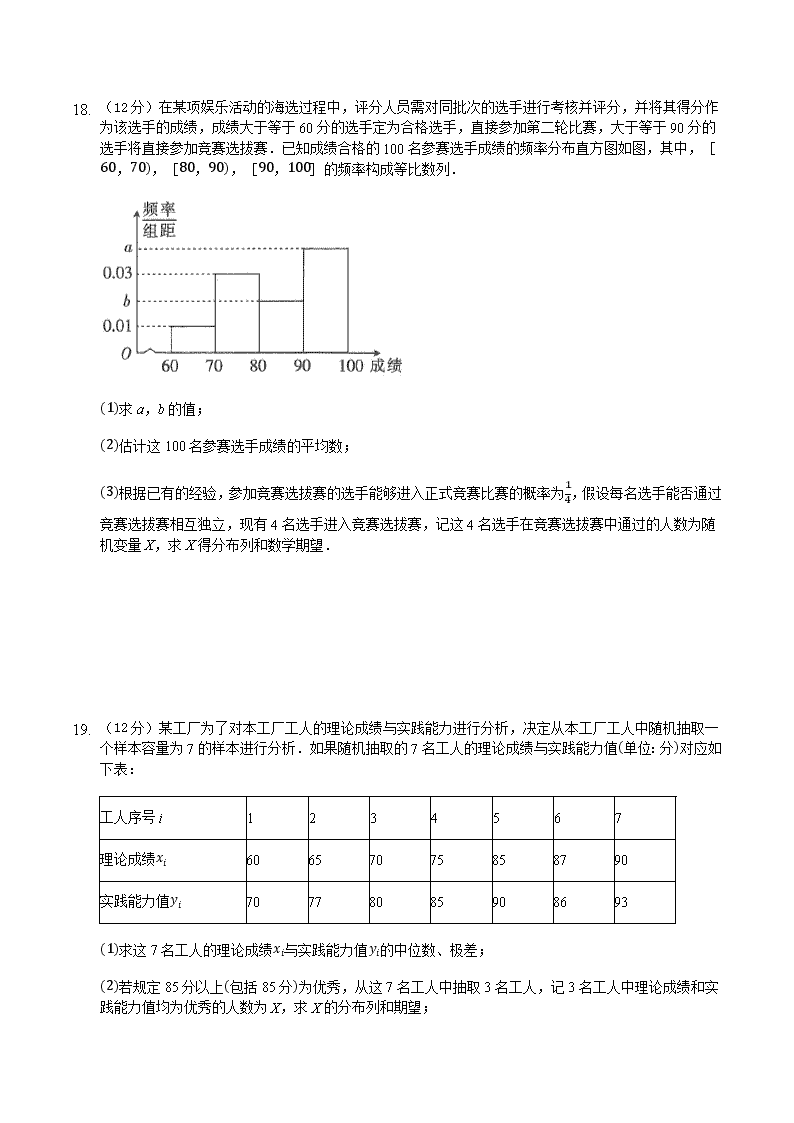
河北省邯郸市永年区第二中学2019-2020学年高二下学期6月考试数学试卷
数学试卷 一、选择题(本大题共12小题,共60.0分) 1. 为了调查某工厂生产的一种产品的尺寸是否合格,现从500件产品中抽出10件进行检验先将500件产品编号为000,001,002,⋯,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读(为了便于说明,下面摘取了随机数表,附表1的第6行至第8行),即第一个号码为439,则选出的第4个号码是( ) 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 A. 548 B. 443 C. 379 D. 217 2. 某学校有高一、高二、高三三个年级,已知高一、高二、高三的学生数之比为2∶3∶5,现从该学校中抽取一个容量为100的样本,从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为14,则该学校学生的总数为( ) A. 200 B. 400 C. 500 D. 1000 3. 从装有3个白球,1个红球(球除颜色外完全相同)的不透明箱子中,不放回地随机取出了3个球,恰好是2个白球,1个红球的概率是( ) A. 34 B. 13 C. 12 D. 16 4. 某校有1000人参加某次模拟考试,其中数学考试成绩近似服从正态分布N105,σ2σ>0,试卷满分150分,统计结果显示数学成绩优秀(高于120分)的人数占总人数的15,则此次数学考试成绩在90分到105分之间的人数约为( ) A. 150 B. 200 C. 300 D. 400 5. 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速的众数、中位数的估计值为( ) A. 62,62.5 B. 65,62 C. 65,63.5 D. 65,65 6. 已知变量x,y之间的线性回归方程为y=-0.5x+15,且变量x,y之间的一组关系数据如下表所示,则下列说法中,正确的个数是( ) x 2 4 6 8 y 14 m 12 11 ①当x=12时,y的值必定为9; ②变量x,y负相关; ③由表格数据知,该回归直线必过点(5,12.5); ④m=12. A. 1 B. 2 C. 3 D. 4 1. 4名学生和3位老师排成一排合影,恰有两位老师相邻的不同排法有( ) A. 240种 B. 2880种 C. 720种 D. 960种 2. 已知(x-1)5=a0+a1(x+1)+a2(x+1)2+…+a5(x+1)5,则a2=( ) A. 20 B. -20 C. 80 D. -80 3. 已知数据x1,x2,…,x10,2的平均数为2,方差为1,则数据x1,x2,…,x10相对于原数据( ) A. 一样稳定 B. 变得比较稳定 C. 变得比较不稳定 D. 稳定性不可以判断 4. 从3,5,7中选两个数字,从0,4,6中选两个数字,组成无重复数字的四位数.其中偶数的个数为( ) A. 36个 B. 72个 C. 82个 D. 96个 5. 3x-23x11的展开式中有理项共有( ) A. 4项 B. 3项 C. 2项 D. 1项 6. 某中学为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛.A,B两队各由4名选手组成,一共进行4局比赛,每局两队各派1名选手进行PK,除第3局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为23,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( ) A. 2027 B. 5281 C. 1627 D. 79 二、填空题(本大题共4小题,共20.0分) 7. 已知随机变量ξ服从正态分布,N1,2,则D2ξ+3=________. 8. (1-2x)5的展开式中含x3的项的系数为________;所有项的系数和为________· 9. 位于数轴原点的一只电子兔沿着数轴按下列规则移动:电子兔每次移动一个单位,移动的方向向左或向右,并且向左移动的概率为23,向右移动的概率为13,则电子兔移动五次后位于点(-1,0)的概率是________. 10. “2019曹娥江国际半程马拉松”在上虞举行,现要选派5名志愿者服务于A、B、C、D四个不同的运动员救助点,每个救助点至少分配一人,若志愿者甲要求不到A救助点,则不同的分配方案有 种. 三、解答题(本大题共6小题,共70.0分) 11. (10分)甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是23,乙班三名同学答对的概率分别是23,23,12,且这六名同学答题正确与否相互之间没有影响. (1)记“甲、乙两班总得分之和是60分”为事件A,求事件A发生的概率; (2)用X表示甲班总得分,求随机变量X的概率分布和数学期望. 1. (12分)在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,大于等于90分的选手将直接参加竞赛选拔赛.已知成绩合格的100名参赛选手成绩的频率分布直方图如图,其中,[60,70),[80,90),[90,100]的频率构成等比数列. (1)求a,b的值; (2)估计这100名参赛选手成绩的平均数; (3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为14,假设每名选手能否通过竞赛选拔赛相互独立,现有4名选手进入竞赛选拔赛,记这4名选手在竞赛选拔赛中通过的人数为随机变量X,求X得分布列和数学期望. 2. (12分)某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值(单位:分)对应如下表: 工人序号i 1 2 3 4 5 6 7 理论成绩xi 60 65 70 75 85 87 90 实践能力值yi 70 77 80 85 90 86 93 (1)求这7名工人的理论成绩xi与实践能力值yi的中位数、极差; (2)若规定85分以上(包括85分)为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望; (3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.(系数精确到0.01) 附:线性回归方程y=bx+a中,b=i=1n(xi-x)(yi-y)i=1n(xi-x)2,a=y-bx. x y i=17xi-x2 i=17xi-xyi-y 76 83 812 526 1. (12分)为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市为拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,对年龄在20∼60岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下: 年龄 [20,28) [28,36) [36,44) [44,52) [52,60) 支持的人数 15 5 15 28 17 (1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异; 44岁以下 44岁及44岁以上 总计 支持 不支持 总计 (2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会.现从这8人中随机抽2人. ①抽到1人是44岁以下时,求抽到的另一人是44岁以上的概率. ②记抽到44岁以上的人数为X,求随机变量X的分布列及数学期望. 参考数据: P(K2≥k0) 0.100 0.050 0.010 0.001 k0 2.706 3.841 6.635 10.828 K2=nad-bc2a+bc+da+cb+d,其中n=a+b+c+d. 1. (12分)为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团. (1)求这4人中恰有1人参加篮球社团的概率; (2)用ξ,η分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为ξ和η之差的绝对值,求随机变量X的分布列与数学期望E(X). 1. (12分)某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理. (Ⅰ)若小店一天购进16份,求当天的利润y(单位:元)关于当天需求量n(单位:份,n∈N)的函数解析式; (Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表: 日需求量 n 14 15 16 17 18 19 20 频数 10 20 16 16 15 13 10 以100天记录的各需求量的频率作为各需求量发生的概率. (i)小店一天购进16份这种食品,X表示当天的利润(单位:元),求X的分布列及数学期望; (ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份? 数学试卷 【答案】 1. D 2. B 3. A 4. C 5. D 6. B 7. B 8. D 9. C 10. D 11. C 12. A 13. 8 14. -80;-1 15. 80243 16. 180 17. 解:(1)P(A)=(23×23×23)×(23×23×12)=16243; (2)随机变量X的取值为0,10,20,30. P(X=0)=C30(1-23)3=127, P(X=10)=C31(1-23)2×23=29, P(X=20)=C32(23)2×(1-23)=49, P(X=30)=C33(23)3=827, 所以,X的概率分布为: X 0 10 20 30 P 127 29 49 827 所以期望E(X)=0×127+10×29+20×49+30×827=20. 18. 解:(1)由题意,0.01+0.03+a+b×10=10.01a=b2 解得a=0.04b=0.02 (2)估计这100名选手的成绩平均数为65×0.1+75×0.3+85×0.2+95×0.4=84. (3)由题意知,X∼B(4,14), 则X可能取值为0,1,1,2,3. 则P(X=i)=C4i(1-14)4-i(14)i. 所以X的分布列为: X 0 1 2 3 4 P 81256 2764 27128 364 1256 故X的数学期望为E(X)=4×14=1. 19. 解:(1)这7名工人的理论成绩xi的中位数为75, 极差为90-60=30; 实践能力值yi的中位数为85,极差为93-70=23. (2)∵7名工人中理论成绩和实践能力值均为优秀的人数为3名, ∴X的所有可能取值为0,1,2,3, 则, , , . ∴X的分布列为 X 0 1 2 3 P 435 1835 1235 135 ∴E(X)=0×435+1×1835+2×1235+3×135=97. (3)由公式得b=i=17(xi-x)(yi-y)i=17(xi-x)2=263406≈0.65, a=y-bx=83-263406×76≈33.77. ∴实践能力值y关于理论成绩x的线性回归方程为y=0.65x+33.77. 20. 解:(1)由统计数据填2×2列联表如下, 44岁以下 44岁及44岁以上 合计 支持 35 45 80 不支持 15 5 20 合计 50 50 100 计算观测值k0=100×(35×5-45×15)250×50×80×20=254=6.25>3.841, 所以在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异; (2)由题意可知抽取的这8人中,44岁以下的有6人,44岁以上的有2人, ①抽到1人是44岁以下的概率为68=34,抽到1人是44岁以下且另一人是44岁以上的概率为. 故所求概率为3734=47. ②根据题意,X的可能取值是0,1,2; 计算P(X=0)=C62C82=1528, P(X=1)=C61⋅C21C82=37, P(X=2)=C22C82=128, 可得随机变量X的分布列为 X 0 1 2 P 1528 37 128 故数学期望为E(X)=0×1528+1×37+2×128=12. 21. 解:(1)依题意,这4个人中,每个人参加篮球社团的概率为13, 参加足球社团的概率为23, 设“这4个人中恰有i个人参加篮球社团”为事件Ai(i=0,1,2,3,4), 则P(Ai)=C4i(13)i(23)4-i,(i=0,1,2,3,4), 这4个人中恰有1个人参加篮球社团的概率为: P(A1)=C41(13)(23)3=3281; (2)由已知得X的所有可能取值为0,2,4, P(X=0)=C42(13)2(23)2=2481=827, P(X=2)=C41(13)(23)3+C43(13)3(23)=4081, P(X=4)=C40(23)4+C44(13)4=1781, ∴X的分布列为: ∴E(X)=0×827+2×4081+4×1781=14881. 22. 解:(Ⅰ)当日需求量n≥16时,利润y=80, 当日需求量n<16时,利润y=5n-4(16-n)=9n-64, 所以y关于n的函数解析式为y=9n-64,n<16,80,n⩾16(n∈N). (Ⅱ)(i)X可能的取值为62,71,80, 并且,P(X=71)=0.2,P(X=80)=0.7. X的分布列为: X 62 71 80 P 0.1 0.2 0.7 X的数学期望为E(X)=62×0.1+71×0.2+80×0.7=76.4元. (ii)若小店一天购进17份食品,Y表示当天的利润(单位:元), 那么Y的分布列为: Y 58 67 76 85 P 0.1 0.2 0.16 0.54 Y的数学期望为E(Y)=58×0.1+67×0.2+76×0.16+85×0.54=77.26元. 由以上的计算结果可以看出,E(X)查看更多