- 2024-01-09 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届广东省广州市越秀区执信中学高二上学期期中数学试卷(文科) (解析版)
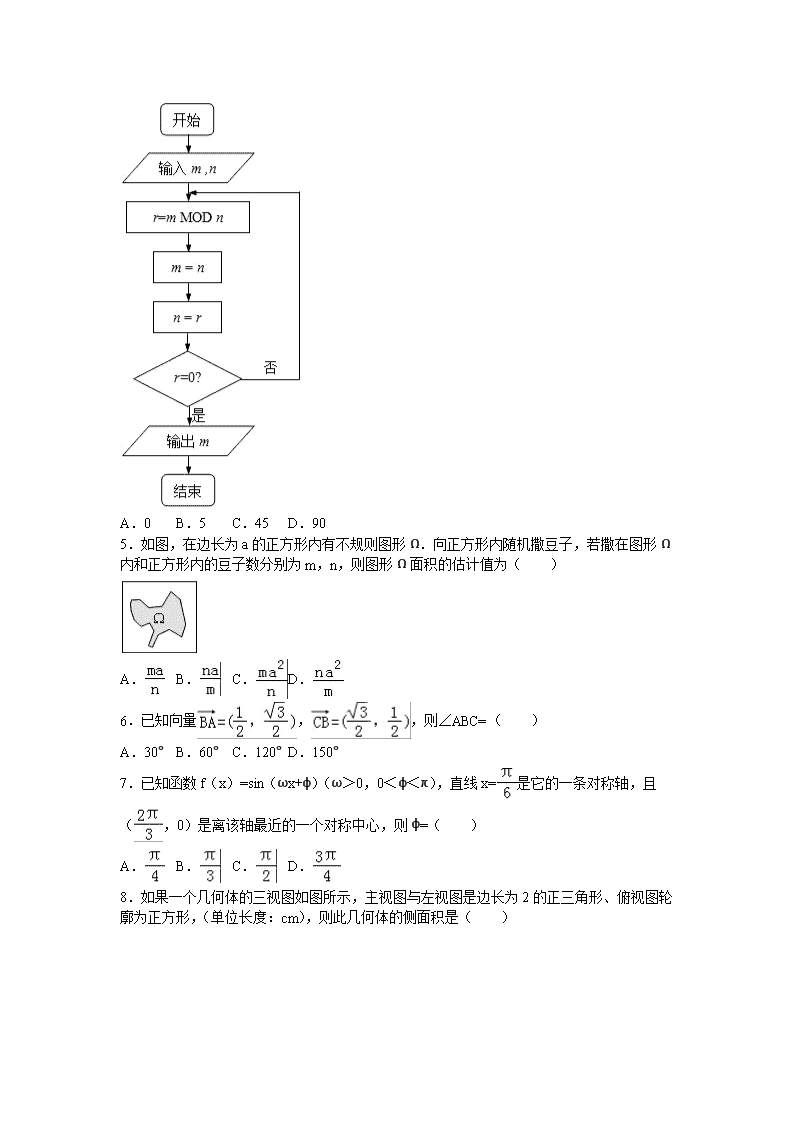
2016-2017学年广东省广州市越秀区执信中学高二(上)期中数学试卷(文科) 一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填涂在答题卡相应的区域. 1.已知集合M={x|﹣1<x<1},N={x|y=},则M∩N=( ) A.{x|0<x<1} B.{x|0≤x<1} C.{x|x≥0} D.{x|﹣1<x≤0} 2.已知下列命题: ①命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1<3x”; ②已知p、q为两个命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”; ③“a>2”是“a>5”的充分不必要条件; ④“若xy=0,则x=0且y=0”的逆否命题为真命题. 其中所有真命题的序号是( ) A.①②③ B.②④ C.② D.④ 3.2014年11月11日的“双十一”又掀购物狂潮,淘宝网站对购物情况做了一项调查,收回的有效问卷共500000份,其中购买下列四种商品的人数统计如下:服饰鞋帽198000人;家居用品94000人;化妆品116000人;家用电器92000人.为了解消费者对商品的满意度,淘宝网站用分层抽样的方法从中选出部分问卷进行调查,已知在购买“化妆品”这一类中抽取了116人,则在购买“家居用品”这一类中应抽取的问卷份数为( ) A.92 B.94 C.116 D.118 4.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( ) A.0 B.5 C.45 D.90 5.如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( ) A. B. C. D. 6.已知向量,,则∠ABC=( ) A.30° B.60° C.120° D.150° 7.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),直线x=是它的一条对称轴,且(,0)是离该轴最近的一个对称中心,则φ=( ) A. B. C. D. 8.如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( ) A. cm2 B. cm2 C.8cm2 D.14cm2 9.给出如下列联表: 患心脏病 患其它病 合 计 高血压 20 10 30 不高血压 30 50 80 合 计 50 60 110 参照公式K2=,P(K2≥10.828)≈0.001,p(K2≥6.635)≈0.001得到的正确结论是( ) A.有99%以上的把握认为“高血压与患心脏病无关” B.有99%以上的把握认为“高血压与患心脏病有关” C.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关” D.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关” 10.已知a>0,b>0,若不等式﹣﹣≤0恒成立,则m的最大值为( ) A.4 B.16 C.9 D.3 11.两定点F1(﹣3,0),F2(3,0),P为曲线=1上任意一点,则( ) A.|PF1|+|PF2|≥10 B.|PF1|+|PF2|≤10 C.|PF1|+|PF2|>10 D.|PF1|+|PF2|<10 12.将正奇数排成如图所示的三角形数阵(第k行有k个奇数),其中第i行第j个数表示为aij,例如a42=15,若aij=2015,则i﹣j=( ) A.26 B.27 C.28 D.29 二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答卷的相应位置 13.如果发现散点图中所有的样本点都在一条直线上,则残差平方和等于 ,解释变量和预报变量之间的相关系数等于 . 14.若方程表示椭圆,则m的取值范围是 . 15.若x,y满足约束条件.则的最大值为 . 16.已知函数y=f(x)是定义在R上的增函数,函数y=f(x﹣1)图象关于点(1,0)对称,若对任意的x,y∈R,不等式f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,则当x>3时,x2+y2的取值范围是 . 三.解答题:必做大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤 17.在△ABC中,角A,B,C所对的边分别为a,b,c,点(a,b)在直线x(sinA﹣sinB)+ysinB=csinC上. (Ⅰ)求角C的值; (Ⅱ)若2cos2﹣2sin2=,且A<B,求. 18.已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列. (1)求数列{an}和{bn}的通项公式; (2)求数列{bn}的前n项和. 19.如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点. (1)在棱PB上是否存在一点Q,使得QM∥面PAD?若存在,指出点Q的位置并证明;若不存在,请说明理由; (2)求点D到平面PAM的距离. 20.某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100﹣110的学生数有21人. (1)求总人数N和分数在110﹣115分的人数n; (2)现准备从分数在110﹣115的n名学生(女生占)中任选2人,求其中恰好含有一名女生的概率; (3)为了分析某个学生的学习状态,对其下一阶段的学生提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩. 数学 88 83 117 92 108 100 112 物理 94 91 108 96 104 101 106 已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程=x+.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少? (参考公式: =, =﹣) 21.已知椭圆+=1(a>b>0)经过点P(,),离心率为,动点 M(2,t)(t>0). (1)求椭圆的标准方程; (2)求以 O M( O为坐标原点)为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程; (3)设F是椭圆的右焦点,过点F作 O M的垂线与以 O M为直径的圆交于点 N,证明线段 O N的长为定值,并求出这个定值. 22.已知函数f(x)=|x|+﹣1(x≠0). (1)当m=2时,判断f(x)在(﹣∞,0)的单调性,并用定义证明. (2)若对任意x∈R,不等式 f(2x)>0恒成立,求m的取值范围; (3)讨论f(x)零点的个数. 2016-2017学年广东省广州市越秀区执信中学高二(上)期中数学试卷(文科) 参考答案与试题解析 一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填涂在答题卡相应的区域. 1.已知集合M={x|﹣1<x<1},N={x|y=},则M∩N=( ) A.{x|0<x<1} B.{x|0≤x<1} C.{x|x≥0} D.{x|﹣1<x≤0} 【考点】交集及其运算. 【分析】求出N中x的范围确定出N,找出M与N的交集即可. 【解答】解:由N中y=,得到x≥0,即N={x|x≥0}, ∵M={x|﹣1<x<1}, ∴M∩N={x|0≤x<1}. 故选:B. 2.已知下列命题: ①命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1<3x”; ②已知p、q为两个命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”; ③“a>2”是“a>5”的充分不必要条件; ④“若xy=0,则x=0且y=0”的逆否命题为真命题. 其中所有真命题的序号是( ) A.①②③ B.②④ C.② D.④ 【考点】命题的真假判断与应用. 【分析】①利用命题的否定即可判断出; ②由“p∨q”为假命题,则p与q都为假命题,可得¬p,¬q都为真命题,即可判断出“¬p∧¬q为真命题”; ③“a>2”是“a>5”的必要不充分条件; ④“若xy=0,则x=0且y=0”是假命题,即可判断出其逆否命题为假命题的真假. 【解答】解:①命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”,因此不正确; ②已知p、q为两个命题,若“p∨q”为假命题,则p与q都为假命题,∴¬p,¬q都为真命题,∴“¬p∧¬q为真命题”,正确; ③“a>2”是“a>5”的必要不充分条件,不正确; ④“若xy=0,则x=0且y=0”是假命题,因其逆否命题为假命题,因此不正确. 综上可得:其中所有真命题的序号是②. 故选:C. 3.2014年11月11日的“双十一”又掀购物狂潮,淘宝网站对购物情况做了一项调查,收回的有效问卷共500000份,其中购买下列四种商品的人数统计如下:服饰鞋帽198000人;家居用品94000人;化妆品116000人;家用电器92000人.为了解消费者对商品的满意度,淘宝网站用分层抽样的方法从中选出部分问卷进行调查,已知在购买“化妆品”这一类中抽取了116人,则在购买“家居用品”这一类中应抽取的问卷份数为( ) A.92 B.94 C.116 D.118 【考点】分层抽样方法. 【分析】根据分层抽样的定义建立比例关系即可得到结论. 【解答】解:在购买“化妆品”这一类中抽取了116人,则在购买“家居用品”这一类中应抽取的问卷份数为x, 则, 解得x=94, 故选:B 4.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( ) A.0 B.5 C.45 D.90 【考点】程序框图. 【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量m的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【解答】解:第一次执行循环体,r=90,m=135,n=90,不满足退出循环的条件; 第二次执行循环体,r=0,m=45,n=0,满足退出循环的条件; 故输出的m值为45, 故选:C 5.如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( ) A. B. C. D. 【考点】几何概型. 【分析】根据落到不规则图形Ω和正方形中的点的个数,得到概率,即得到两者的面积的比值,根据所给的正方形的边长,求出面积,根据比值得到要求的面积的估计值. 【解答】解:∵由题意知在正方形中随机投掷n个点,若n个点中有m点落入Ω中, ∴不规则图形Ω的面积:正方形的面积=m:n ∴不规则图形Ω的面积=×正方形的面积 =×a2 =. 故选C. 6.已知向量,,则∠ABC=( ) A.30° B.60° C.120° D.150° 【考点】数量积表示两个向量的夹角. 【分析】由题意可得, =(﹣,﹣),||=1,||=1,再利用两个向量的数量积公式、两个向量的数量积的定义求得 cos∠ABC 的值,可得∠ABC 的值. 【解答】解:∵向量,,∴=(﹣,﹣),||=1,||=1, ∴=﹣•+•(﹣)=1×1×cos∠ABC,∴cos∠ABC=﹣,∴∠ABC=150°, 故选:D. 7.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),直线x=是它的一条对称轴,且(,0)是离该轴最近的一个对称中心,则φ=( ) A. B. C. D. 【考点】正弦函数的图象. 【分析】根据题意,利用求出ω的值,再根据函数f(x)图象过点(,0)求出φ的值. 【解答】解:根据题意, =﹣=, ∴T=2π, ∴ω=1; 又函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)图象过点(,0), ∴sin(+φ)=0, +φ=kπ,k∈Z; 解得φ=kπ﹣,k∈Z; 当k=1时,φ=满足题意. 故选:B. 8.如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( ) A. cm2 B. cm2 C.8cm2 D.14cm2 【考点】由三视图求面积、体积. 【分析】根据已知中几何体的三视图中,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形我们可以求出该正四棱锥的底面上的棱长和侧面的高,代入棱锥侧面积公式 即可得到答案. 【解答】解:由已知中的三视图,我们可以得到 该几何体是一个正四棱锥, 又由主视图与左视图是边长为2的正三角形可得棱锥的底面上的棱长为2,棱锥的高为 则棱锥的侧高(侧面的高)为2 故棱锥的侧面积S=4×=8cm2 故选C 9.给出如下列联表: 患心脏病 患其它病 合 计 高血压 20 10 30 不高血压 30 50 80 合 计 50 60 110 参照公式K2=,P(K2≥10.828)≈0.001,p(K2≥6.635)≈0.001得到的正确结论是( ) A.有99%以上的把握认为“高血压与患心脏病无关” B.有99%以上的把握认为“高血压与患心脏病有关” C.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关” D.在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关” 【考点】独立性检验. 【分析】由P(K2≥6.635)≈0.010得到统计结论. 【解答】解:因为P(K2≥10.828)≈0.001,p(K2≥6.635)≈0.001, 所以有99%以上的把握认为“高血压与患心脏病有关”. 故选:B. 10.已知a>0,b>0,若不等式﹣﹣≤0恒成立,则m的最大值为( ) A.4 B.16 C.9 D.3 【考点】基本不等式. 【分析】不等式恒成立⇒的最小值,利用不等式的基本性质求出即可. 【解答】解:不等式恒成立⇒的最小值, ∵a>0,b>0, =10+≥10+=16,当且仅当,即a=b时取等号. ∴m≤16,即m的最大值为16. 故选B. 11.两定点F1(﹣3,0),F2(3,0),P为曲线=1上任意一点,则( ) A.|PF1|+|PF2|≥10 B.|PF1|+|PF2|≤10 C.|PF1|+|PF2|>10 D.|PF1|+|PF2|<10 【考点】曲线与方程. 【分析】根据题意,曲线=1表示的图形是图形是以A(﹣5,0),B(0,4),C(5,0),D(0,﹣4)为顶点的菱形,而满足|PF1|+|PF2|=10的点的轨迹恰好是以A、B、C、D为顶点的椭圆,由此结合椭圆的定义即可得到|PF1|+|PF2|≤10. 【解答】解:∵F1(﹣3,0),F2(3,0), ∴满足|PF1|+|PF2|=10的点在以F1、F2为焦点, 2a=10的椭圆上 可得椭圆的方程为, ∵曲线=1表示的图形是图形是以A(﹣5,0), B(0,4),C(5,0),D(0,﹣4)为顶点的菱形 ∴菱形ABCD的所有点都不在椭圆的外部, 因此,曲线=1上的点P,必定满足|PF1|+|PF2|≤10 故选:B. 12.将正奇数排成如图所示的三角形数阵(第k行有k个奇数),其中第i行第j个数表示为aij,例如a42=15,若aij=2015,则i﹣j=( ) A.26 B.27 C.28 D.29 【考点】归纳推理. 【分析】分析正奇数排列的正三角图表知,第i行(其中i∈N*)有i个奇数,且从左到右按从小到大的顺序排列,则2015是第1008个奇数,由等差数列的知识可得,它排在第几行第几个数 【解答】解:根据正奇数排列的正三角图表知,2015是第1008个奇数,应排在i行(其中i∈N*), 则1+2+3+…+(i﹣1)=i(i﹣1)≤1008①, 且1+2+3+…+i=i(i+1)>1008②; 验证i=45时,①②式成立,所以i=45; 第45行第1个奇数是2××44×45+1=1981, 而1981+2(j﹣1)=2015, ∴j=18; ∴i﹣j=45﹣18=27. 故选:B 二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答卷的相应位置 13.如果发现散点图中所有的样本点都在一条直线上,则残差平方和等于 0 ,解释变量和预报变量之间的相关系数等于 1或﹣1 . 【考点】回归分析. 【分析】根据残差,残差平方和,和相关系数的定义和性质即可得到结论. 【解答】解:设样本点为(xi,yi),i=1,2,3,…n,回归直线为;若散点图中所有的样本点都在一条直线上,则此直线方程就是回归直线方程.所以有;残差平方和;解释变量和预报变量之间的相关系数R满足,∴R=±1. 故答案为0,1或﹣1. 14.若方程表示椭圆,则m的取值范围是 (1,2)∪(2,3) . 【考点】椭圆的简单性质. 【分析】由于方程表示椭圆,可得,即可. 【解答】解:∵方程表示椭圆,∴,解得1<m<3,且m≠2. 故答案为(1,2)∪(2,3). 15.若x,y满足约束条件.则的最大值为 3 . 【考点】简单线性规划. 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值. 【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC). 设k=,则k的几何意义为区域内的点到原点的斜率, 由图象知OA的斜率最大, 由,解得,即A(1,3), 则kOA==3, 即的最大值为3. 故答案为:3. 16.已知函数y=f(x)是定义在R上的增函数,函数y=f(x﹣1)图象关于点(1,0)对称,若对任意的x,y∈R,不等式f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,则当x>3时,x2+y2的取值范围是 (13,49) . 【考点】函数恒成立问题;函数单调性的性质;函数的图象. 【分析】由函数y=f(x﹣1)的图象关于点(1,0)对称,结合图象平移的知识可知函数y=f(x)的图象关于点(0,0)对称,从而可知函数y=f(x)为奇函数,由f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,可把问题转化为(x﹣3)2+(y﹣4)2<4,借助于的有关知识可求. 【解答】解:∵函数y=f(x﹣1)的图象关于点(1,0)对称, ∴函数y=f(x)的图象关于点(0,0)对称, 即函数y=f(x)为奇函数,则f(﹣x)=﹣f(x), 又∵f(x)是定义在R上的增函数且f(x2﹣6x+21)+f(y2﹣8y)<0恒成立 ∴f(x2﹣6x+21)<﹣f(y2﹣8y)=f(8y﹣y2)恒成立, ∴x2﹣6x+21<8y﹣y2, ∴(x﹣3)2+(y﹣4)2<4恒成立, 设M (x,y),则当x>3时,M表示以(3,4)为圆心2为半径的右半圆内的任意一点, 则d=表示区域内的点和原点的距离. 由下图可知:d的最小值是OA=, OB=OC+CB,5+2=7, 当x>3时,x2+y2的范围为(13,49). 故答案为:(13,49). 三.解答题:必做大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤 17.在△ABC中,角A,B,C所对的边分别为a,b,c,点(a,b)在直线x(sinA﹣sinB)+ysinB=csinC上. (Ⅰ)求角C的值; (Ⅱ)若2cos2﹣2sin2=,且A<B,求. 【考点】正弦定理;余弦定理. 【分析】(Ⅰ)已知等式利用正弦定理化简,利用余弦定理表示出cosC,将得出的关系式代入求出cosC的值,即可确定出角C的值; (Ⅱ)已知等式左边利用二倍角的余弦函数公式化简,将表示出的B代入利用两角和与差的余弦函数公式化简,整理后求出利用特殊角的三角函数值求出A的度数,进而求出C的度数,原式利用正弦定理化简,将sinA与sinC的值代入计算即可求出值. 【解答】解:(Ⅰ)将(a,b)代入直线解析式得:a(sinA﹣sinB)+bsinB=csinC, 由正弦定理==得:a(a﹣b)+b2=c2,即a2+b2﹣c2=ab, 由余弦定理得cosC==, ∵0<C<π, ∴C=; (Ⅱ)∵2cos2﹣2sin2=1+cosA﹣1+cosB=cosA+cos(﹣A)=cosA+sinA=sin(A+)=, ∵A+B=,且A<B, ∴0<A<, ∴<A+<,即A+=, ∴A=,B=,C=, 则===. 18.已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列. (1)求数列{an}和{bn}的通项公式; (2)求数列{bn}的前n项和. 【考点】数列的求和;数列递推式. 【分析】(1)利用等差数列、等比数列的通项公式先求得公差和公比,即可求数列的通项公式; (2)利用分组求和的方法求解数列的和,由等差数列及等比数列的前n项和公式即可求解数列的和. 【解答】解:(1)设等差数列{an}的公差为d,由题意得 d===3. ∴an=a1+(n﹣1)d=3n(n=1,2,…). ∴数列{an}的通项公式为:an=3n; 设等比数列{bn﹣an}的公比为q,由题意得: q3===8,解得q=2. ∴bn﹣an=(b1﹣a1)qn﹣1=2n﹣1. 从而bn=3n+2n﹣1(n=1,2,…). ∴数列{bn}的通项公式为:bn=3n+2n﹣1; (2)由(1)知bn=3n+2n﹣1(n=1,2,…). 数列{3n}的前n项和为n(n+1),数列{2n﹣1}的前n项和为=2n﹣1. ∴数列{bn}的前n项和为n(n+1)+2n﹣1. 19.如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点. (1)在棱PB上是否存在一点Q,使得QM∥面PAD?若存在,指出点Q的位置并证明;若不存在,请说明理由; (2)求点D到平面PAM的距离. 【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定;点、线、面间的距离计算. 【分析】(1)取棱PB的中点Q,连结QM,QA,又M为PC的中点,证明QM∥AD,利用直线与平面平行的判定定理证明QM∥面PAD. (2)设点D到平面PAC的距离为h,由VD﹣PAC=VP﹣ACD,通过证明以及计算即可求点D到平面PAM的距离. 【解答】解:(1)当点Q为棱PB的中点时,QM∥面PAD,证明如下 … 取棱PB的中点Q,连结QM,QA,又M为PC的中点, 所以, 在菱形ABCD中AD∥BC可得QM∥AD… 又QM⊄面PAD,AD⊂面PAD 所以QM∥面PAD… (2)点D到平面PAM的距离即点D到平面PAC的距离, 由(Ⅰ)可知PO⊥AD,又平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD,PO⊂平面PAD,所以PO⊥平面ABCD, 即PO为三棱锥P﹣ACD的体高.… 在Rt△POC中,,, 在△PAC中,PA=AC=2,,边PC上的高AM=, 所以△PAC的面积,… 设点D到平面PAC的距离为h, 由VD﹣PAC=VP﹣ACD得 … ,又,所以,… 解得,所以点D到平面PAM的距离为.… 20.某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100﹣110的学生数有21人. (1)求总人数N和分数在110﹣115分的人数n; (2)现准备从分数在110﹣115的n名学生(女生占)中任选2人,求其中恰好含有一名女生的概率; (3)为了分析某个学生的学习状态,对其下一阶段的学生提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩. 数学 88 83 117 92 108 100 112 物理 94 91 108 96 104 101 106 已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程=x+.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少? (参考公式: =, =﹣) 【考点】线性回归方程. 【分析】(1)求出该班总人数、分数在110﹣115内的学生的频率,即可得出分数在110﹣115内的人数; (2)利用列举法确定基本事件的个数,即可求出其中恰好含有一名女生的概率; (3)分别求出回归学生的值,代入从而求出线性回归方程,将x=130代入,从而求出y的值. 【解答】解:(1)分数在100﹣110内的学生的频率为P1=(0.04+0.03)×5=0.35,… 所以该班总人数为N==60,… 分数在110﹣115内的学生的频率为P2=1﹣(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1,分数在110﹣115内的人数n=60×0.1=6..… (2)由题意分数在110﹣115内有6名学生,其中女生有2名, 设男生为A1,A2,A3,A4,女生为B1,B2, 从6名学生中选出3人的基本事件为: (A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2), (A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4), (A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)共15个. 其中恰 好含有一名女生的基本事件为 (A1,B1),(A1,B2),(A2,B2),(A2,B1),(A3,B1), (A3,B2),(A4,B1),(A4,B2),共8个, 所以所求的概率为P=.… (3)=100, =100;… 由于x与y之间具有线性相关关系,根据回归系数公式得到 ==0.5, =100﹣0.5×100=50,∴线性回归方程为=0.5x+50,… ∴当x=130时, =115.… 21.已知椭圆+=1(a>b>0)经过点P(,),离心率为,动点 M(2,t)(t>0). (1)求椭圆的标准方程; (2)求以 O M( O为坐标原点)为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程; (3)设F是椭圆的右焦点,过点F作 O M的垂线与以 O M为直径的圆交于点 N,证明线段 O N的长为定值,并求出这个定值. 【考点】椭圆的简单性质. 【分析】(1)把点代入椭圆方程可得,又,a2=b2+c2,联立解出即可得出; (2)以OM为直径的圆的圆心为,半径,可得圆的标准方程;由于以OM为直径的圆被直线3x﹣4y﹣5=0截得的弦长为2,利用点到直线的距离公式可得圆心到直线3x﹣4y﹣5=0的距离d,利用弦长公式可得弦长=2即可得出. (3)方法一:过点F作OM的垂线,垂足设为K.直线OM的方程为,直线FN的方程为,联立解得K坐标,可得|OK|,|OM|,利用|ON|2=|OK|•|OM|即可证明. 方法二:设N(x0,y0),则,,,.利用,,可证为定值. 【解答】(1)解:由题意得,① ∵椭圆经过点,∴② 又a2=b2+c2③ 由①②③解得a2=2,b2=c2=1. ∴椭圆的方程为. (2)解:以OM为直径的圆的圆心为,半径, 故圆的方程为. ∵以OM为直径的圆被直线3x﹣4y﹣5=0截得的弦长为2, ∴圆心到直线3x﹣4y﹣5=0的距离. ∴,即2|2t+2|=5t, 故4t+4=5t,或4t+4=﹣5t, 解得t=4,或. 又t>0,故t=4. 所求圆的方程为(x﹣1)2+(y﹣2)2=5. (3)证明:方法一:过点F作OM的垂线,垂足设为K. 直线OM的方程为,直线FN的方程为. 由,解得,故. ∴; . 又. ∴. ∴线段ON的长为定值. 方法二:设N(x0,y0),则,,,. ∵,∴2(x0﹣1)+ty0=0.∴2x0+ty0=2. 又∵,∴x0(x0﹣2)+y0(y0﹣t)=0. ∴. ∴为定值. 22.已知函数f(x)=|x|+﹣1(x≠0). (1)当m=2时,判断f(x)在(﹣∞,0)的单调性,并用定义证明. (2)若对任意x∈R,不等式 f(2x)>0恒成立,求m的取值范围; (3)讨论f(x)零点的个数. 【考点】函数恒成立问题;函数零点的判定定理;利用导数研究函数的单调性. 【分析】(1)当m=2时,利用函数单调性的定义即可判断f(x)在(﹣∞,0)的单调性,并用定义证明. (2)利用参数分离法将不等式 f(2x)>0恒成立,进行转化,求m的取值范围; (3)根据函数的单调性和最值,即可得到结论. 【解答】解:(1)当m=2,且x<0时,是单调递减的. 证明:设x1<x2<0,则=== 又x1<x2<0,所以x2﹣x1>0,x1x2>0, 所以 所以f(x1)﹣f(x2)>0,即f(x1)>f(x2), 故当m=2时,在(﹣∞,0)上单调递减的. (2)由f(2x)>0得, 变形为(2x)2﹣2x+m>0,即m>2x﹣(2x)2 而, 当即x=﹣1时, 所以. (3)由f(x)=0可得x|x|﹣x+m=0(x≠0),变为m=﹣x|x|+x(x≠0) 令 作y=g(x)的图象及直线y=m,由图象可得: 当或时,f(x)有1个零点. 当或m=0或时,f(x)有2个零点; 当或时,f(x)有3个零点. 2016年12月10日查看更多