数学(文)卷·2017届山东省泰安市高三第二轮复习质量检测(二模)(2017
高三第二轮复习质量检测
数 学 试 题(文科)
2017.4
一、选择题:(本大题共10个小题,每小题5分。共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.复数满足,则z等于
A. B. C.2-2i D.2+2i
2.设全集U=R,集合,集合,则p应该满足的条件是
A.p>l B.p≥1 C.p
b>0,则
B.向量共线的充要条件是m=0
C.命题“”的否定是“”
D.已知函数在区间[a,b]上的图象是连续不断的,则命题“若,则在区间(a,b)内至少有一个零点”的逆命题为假命题
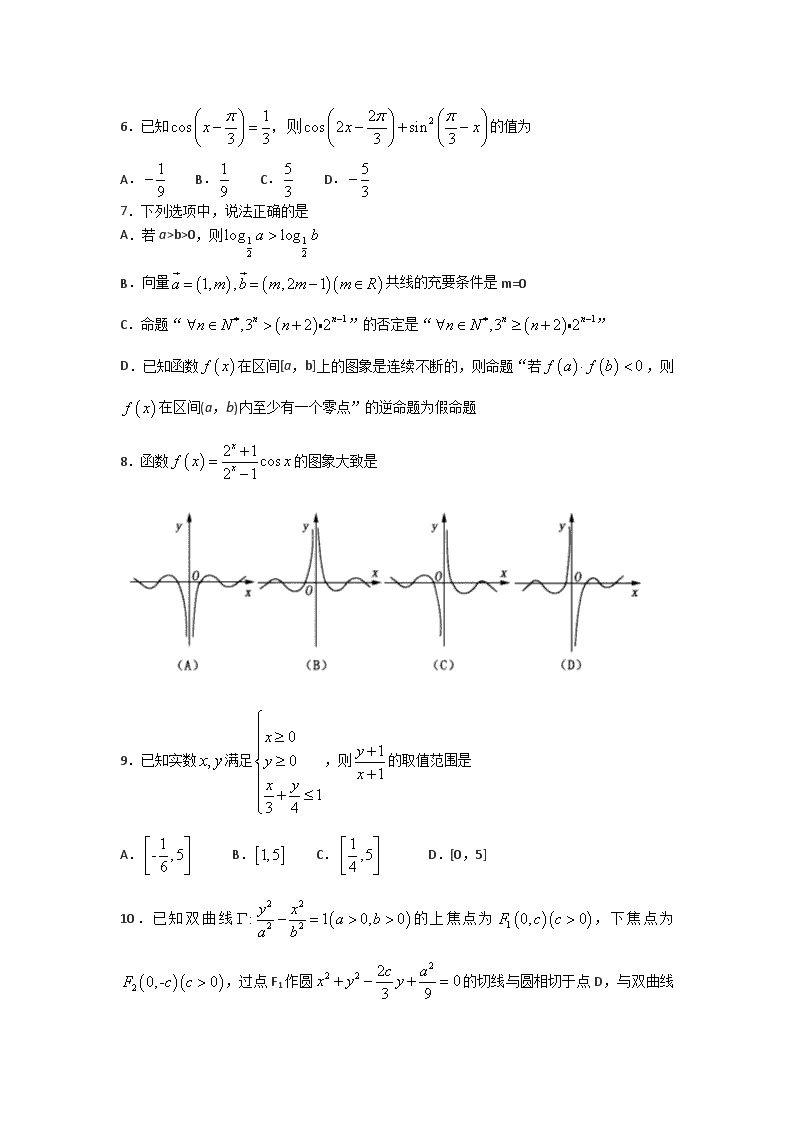
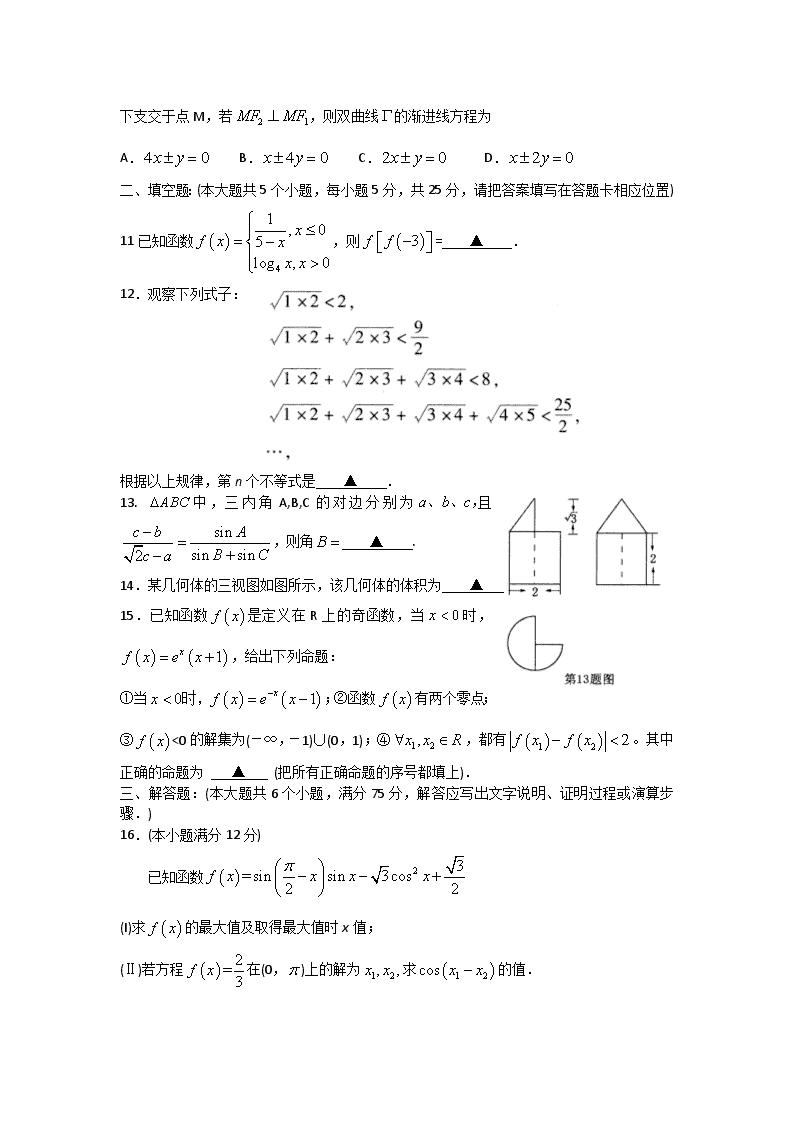
8.函数的图象大致是
9.已知实数满足,则的取值范围是
A. B. C. D.[0,5]
10.已知双曲线的上焦点为,下焦点为,过点F1作圆
的切线与圆相切于点D,与双曲线下支交于点M,若,则双曲线的渐进线方程为
A. B. C. D.
二、填空题:(本大题共5个小题,每小题5分,共25分,请把答案填写在答题卡相应位置)
11已知函数,则= ▲ .
12.观察下列式子:
根据以上规律,第n个不等式是 ▲ .
13. 中,三内角A,B,C的对边分别为且,则角 ▲ .
14.某几何体的三视图如图所示,该几何体的体积为 ▲ .
15.已知函数是定义在R上的奇函数,当时,,给出下列命题:
①当;②函数有两个零点;③<0的解集为(-∞,-1)∪(0,1);④,都有。其中正确的命题为 ▲ (把所有正确命题的序号都填上).
三、解答题:(本大题共6个小题,满分75分,解答应写出文字说明、证明过程或演算步 骤.)
16.(本小题满分12分)
已知函数
(I)求的最大值及取得最大值时x值;
(Ⅱ)若方程在(0,)上的解为求的值.
17.(本小题满分12分)
袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2,3,4的红球,2个编号为A、B的黑球,现从中任取2个小球.
(I)求所取取2个小球都是红球的概率;
(Ⅱ)求所取的2个小球颜色不相同的概率.
18.(本小题满分12分)
如图所示,梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.
(I)求证:EM∥平面ADF;
(Ⅱ)若EFCF,求证ACBD.
19.(本小题满分12分)
已知数列的首项为1, 为数列的前n项和,且满足,其中q> 0,n∈N,又2a2,a3,a2+2成等差数列.
(I)求数列的通项公式;
(Ⅱ)记,若数列为递增数列,求的取值范围.
20.(本小题满分13分)
已知函数.
(I)讨论函数的单调性;
(II)当m>0时,若对于区间[1,2]上的任意两个实数,且,都有成立,求实数m的最大值.
21.(本小题满分14分)
已知椭圆C: (a>b>0)的离心率为,短轴长为2.直线l:与椭圆C交于M、N两点,又l与直线分别交于A、B两点,其中点A在第一象限,点B在第二象限,且△OAB的面积为2(O为坐标原点).
(I)求椭圆C的方程;
(Ⅱ)求的取值范围.