- 2024-01-07 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2008年浙江省金华市初中毕业生学业水平考试数学试题卷及参考答案
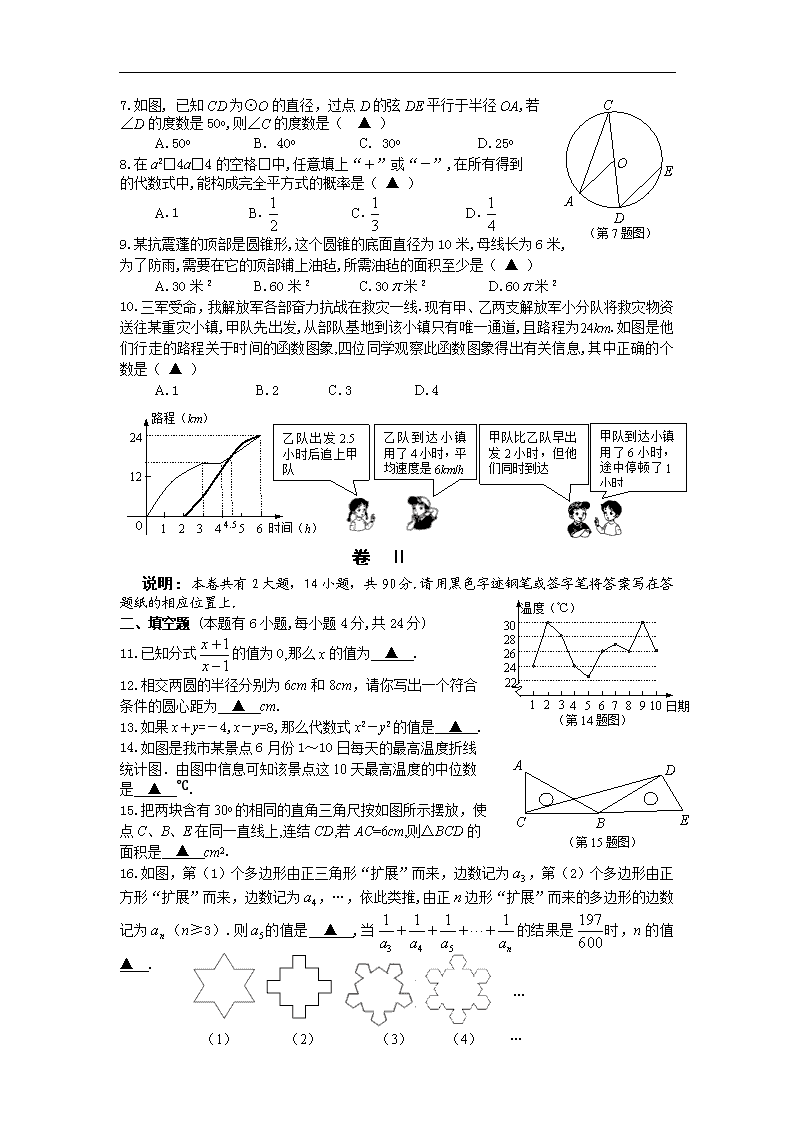
浙江省2008年初中毕业生学业水平考试(金华卷) 数 学 试 题 卷 考生须知: 1.全卷共三大题,24小题,满分为120分.考试时间为100分钟,本次考试采用开卷形式. 2.全卷分试卷Ⅰ(选择题)和试卷Ⅱ(非选择题)两部分,全部在答题纸上作答.卷Ⅰ的答案必须用2B铅笔填涂;卷Ⅱ的答案必须用黑色字迹钢笔或签字笔答在答题纸的相应位置上. 3.请用黑色字迹钢笔或签字笔在答题纸上填写姓名和准考证号. 4.作图时,可先使用2B铅笔,确定后必须使用黑色字迹的钢笔或签字笔描黑. 卷 Ⅰ 说明:本卷共有1大题,10小题,共30分.请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满. 一、选择题(本题有10小题,每小题3分,共30分) 1.如果+3吨表示运入仓库的大米吨数, 那么运出5吨大米表示为( ▲ ) A.-5吨 B.+5吨 C.-3吨 D.+3吨 2.化简的最后结果是( ▲ ) A.2a+2b B.2b C.2a D.0 3.在生活和生产实践中,我们经常需要运用三视图来描述物体的形状和大小.小亮在观察左边的热水瓶时,得到的左视图是( ▲ ) A B C D 主视方向 4.2008年5月12日,在四川省汶川县发生8.0级特大地震,能够准确表示汶川这个地点位置的是( ▲ ) A.北纬31o B.东经103.5o C.金华的西北方向上 D.北纬31o,东经103.5o 包装机 甲 乙 丙 方差(克2) 1.70 2.29 7.22 5.金华火腿闻名遐迩.某火腿公司有甲、乙、丙三台切割包装机,同时分装质量为500克的火腿心片.现从它们分装的火腿心片中各随机抽取10盒,经称量并计算得到质量的方差如表所示,你认为包装质量最稳定的切割包装机是( ▲ ) A B P D (第6题图) C C A.甲 B.乙 C.丙 D.不能确定 6.如图是小明设计用手电来测量某古城墙高度的示意图.点P处 放一水平的平面镜, 光线从点A出发经平面镜反射后刚好射到 古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD, 且测得 AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( ▲ ) A. 6米 B. 8米 C. 18米 D.24米 E A O D C (第7题图) 7.如图, 已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若 ∠D的度数是50o,则∠C的度数是( ▲ ) A.50o B. 40o C. 30o D.25o 8.在a2□4a□4的空格□中,任意填上“+”或“-”,在所有得到 的代数式中,能构成完全平方式的概率是( ▲ ) A.1 B. C. D. 9.某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为10米,母线长为6米, 为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是( ▲ ) A.30米2 B.60米2 C.30米2 D.60米2 10.三军受命,我解放军各部奋力抗战在救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到该小镇只有唯一通道,且路程为24km.如图是他们行走的路程关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( ▲ ) A.1 B.2 C.3 D.4 甲队到达小镇用了6小时,途中停顿了1小时 甲队比乙队早出发2小时,但他们同时到达 乙队出发2.5小时后追上甲队 乙队到达小镇用了4小时,平均速度是6km/h 1 2 3 4 5 6 时间(h) 24 0 4.5 12 路程(km) 卷 Ⅱ 日期 22 24 26 28 30 温度(℃) 2 3 4 5 1 6 7 8 9 10 (第14题图) 说明:本卷共有2大题,14小题,共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸的相应位置上. 二、填空题 (本题有6小题,每小题4分,共24分) 11.已知分式的值为0,那么x的值为 ▲ . 12.相交两圆的半径分别为6cm和8cm,请你写出一个符合 条件的圆心距为 ▲ cm. 13.如果x+y=-4,x-y=8,那么代数式x2-y2的值是 ▲ . A C B D E (第15题图) 14.如图是我市某景点6月份1~10日每天的最高温度折线 统计图.由图中信息可知该景点这10天最高温度的中位数 是 ▲ ℃. 15.把两块含有30o的相同的直角三角尺按如图所示摆放,使 点C、B、E在同一直线上,连结CD,若AC=6cm,则△BCD的 面积是 ▲ cm2. (1) (2) (3) (4) … … 16.如图,第(1)个多边形由正三角形“扩展”而来,边数记为,第(2)个多边形由正方形“扩展”而来,边数记为,…,依此类推,由正边形“扩展”而来的多边形的边数记为(n≥3).则的值是 ▲ ,当的结果是时,n的值 ▲ . 三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程) 17.(本题6分) (1)计算: (2)解不等式:5x-3<1-3x 18.(本题6分) 如图,在△ABC 和△DCB中,AC与BD相交于点O,AB=DC,AC=BD. A B C D O (1)求证: △ABC≌△DCB; (2)△OBC的形状是 ▲ (直接写出结论,不需证明). 1 1 -1 2 A B C O x y · A' 19.(本题6分) 在平面直角坐标系中, △ABC的三个顶点的位置如 图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点 A变换为点A', 点B′、C′分别是B、C的对应点. (1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标: B′ (▲) 、C′ (▲) ; (2)若△ABC 内部一点P的坐标为(a,b),则点P的对应点P ′的坐标是 (▲) . (温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!) 20.(本题8分) A B C O E D 如图, CD切⊙O于点D,连结OC, 交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为10,sin∠COD=. 求:(1)弦AB的长; (2)CD的长; (3)劣弧AB的长(结果保留三个有效数字, sin53.13o ≈0.8, ≈3.142). 21.(本题8分) 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9. (1)求该抛物线的解析式; · A O B D E F x y (2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高; (3)如果身高为1.4米的小丽站在OD之间,且离 点O的距离为t米, 绳子甩到最高处时超过她的头 顶,请结合图像,写出t的取值范围 ▲ . 22.(本题10分) 九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图. 九(3)班“绿色奥运”知识竞赛成绩 频数分布直方图 54.5 64.5 74.5 84.5 94.5 频数(人) 成绩(分) 0 2 4 6 8 10 12 14 9 10 14 九(3)班“绿色奥运”知识竞赛成绩频数分布表 分数段(分) 49.5~ 59.5 59.5~ 69.5 69.5~ 79.5 79.5~ 89.5 89.5~ 99.5 组中值(分) 54.5 64.5 74.5 84.5 94.5 频数 a 9 10 14 5 频率 0.050 0.225 0.250 0.350 b (1)频数分布表中a= ▲ ,b= ▲ ; (2)把频数分布直方图补充完整; x y B A O 图1 (3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖, 一等奖奖励作业本15本及奖金50元, 二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金. 23.(本题10分) 如图1,已知双曲线与直线交于A,B 两点,点A在第一象限.试解答下列问题: (1)若点A的坐标为(4,2),则点B的坐标为 ▲ ;若点A 的横坐标为m, 则点B的坐标可表示为 ▲ ; B A O P Q 图2 (2)如图2,过原点O作另一条直线l,交双曲线于 P,Q两点,点P在第一象限. ①说明四边形APBQ一定是平行四边形; ②设点A,P的横坐标分别为m,n, 四边形APBQ可能是矩形吗? 可能是正方形吗?若可能, 直接写出m,n应满足的条件;若不 可能,请说明理由. 24.(本题12分) 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A 的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD. (1)求直线AB的解析式; (2)当点P运动到点(,0)时,求此时DP的长及点D的坐标; 图1 x y B A O D P 图2 x y B A O (3)是否存在点P,使△OPD的面积等于,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. 浙江省2008年初中毕业生学业水平考试(金华卷) 数学试卷参考答案及评分标准 一、 选择题(本题共10小题,每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案 A C B D A B D B C D 评分标准 选对一题给3分,不选,多选,错选均不给分 二、填空题(本题有6小题,每小题4分,共24分) 11.-1 12. 答案不唯一,只要填一个大于2且小于14的实数均可 13. -32 14. 26 15. 27 16. 30,199(各2分) 三、解答题(本题有8小题,共66分) 17.(本题6分) 解:(1) 原式= -1+ ……(2分) =1 ……(1分) (2)移项得 5x+3x<1+3, ……(1分) 合并同类项得 8x<4, ……(1分) 两边同除以8得 x< ……(1分) 18.(本题6分) (1)证明:在△ABC和△DCB中, ……(3分) ∴△ABC≌△DCB(SSS) ……(1分) (2)等腰三角形 ……(2分) 19.(本题6分) 1 1 A B C O x y · A' C' B' 解:(1)如图,△A'B'C'就是所求的像 ……(3分) (-4, 1) 、(-1,-1) ……(2分) (2) (a-5,b-2) ……(1分) 20.(本题8分) 解:(1)∵ AB⊥OD, ∴∠OEB=900 在Rt△OEB中,BE=OB×sin∠COD=10×=8 由垂径定理得AB=2BE=16 所以弦AB的长是16 ……(2分) (2)方法(一) 在Rt△OEB中, OE= =6. ∵CD切⊙O于点D, ∴∠ODC=900, ∴∠OEB=∠ODC. ∵∠BOE=∠COD, ∴△BOE∽△COD, ∴ , ∴ , ∴CD= . 所以CD的长是 ……(3分) 方法(二)由sin∠COD= 可得tan∠COD= , 在Rt△ODC中,tan∠COD= , ∴CD=OD•tan∠COD=10×= ……(3分) (3)连结OA. 在Rt△ODC中, ∵sin53.13o ≈0.8 ∴∠DOC=53.13o ∴∠AOB=106.26o , ∴劣弧AB的长度 ≈18.5 ……(3分) 21.(本题8分) 解:(1)由题意得点E(1,1.4), B(6,0.9), 代入y=ax2+bx+0.9得 ……(2分) 解得 ……(1分) ∴所求的抛物线的解析式是y=-0.1x2+0.6x+0.9. ……(1分) (2)把x=3代入y=-0.1x2+0.6x+0.9得 y=-0.1×32+0.6×3+0.9=1.8 ∴小华的身高是1.8米 ……(2分) (3)1<t<5 ……(2分) 22.(本题10分) 解:(1)2 ,0.125 ; ……(各2分) (2)图略; ……(2分) (3)由表得,有29名同学获得一等奖或二等奖. 设有x名同学获得一等奖, 则有(29-x)名同学获得二等奖,根据题意得 ……(2分) 解得 x=9 ……(1分) ∴ 50x+30(29-x)=1050 所以他们得到的奖金是1050元 ……(1分) 23.(本题10分) 解:(1)(-4,-2) ……(2分) (-m,-k'm)或 (-m, ) ……(只要写出一种表示方法就得2分) (2)① 由勾股定理OA= , OB= = , ∴OA=OB 同理可得OP=OQ, 所以四边形APBQ一定是平行四边形. ……(2分) ②四边形APBQ可能是矩形 ……(1分) m,n应满足的条件是mn=k ……(1分) 四边形APBQ不可能是正方形 ……(1分) 理由:点A,P不可能达到坐标轴,即∠POA≠900. ……(1分) 24.(本题12分) (1)如图,过点B作BE⊥y轴于点E,作BF⊥x 轴于点F.由已知得 BF=OE=2, OF= = ∴点B的坐标是( ,2) ……(1分) 设直线AB的解析式是y=kx+b,则有 解得 ……(2分) ∴直线AB的解析式是y= x+4 ……(1分) (2) 如图,∵△ABD由△AOP旋转得到, ∴△ABD≌△AOP, ∴AP=AD, ∠DAB=∠PAO,∴∠DAP=∠BAO=600, ∴△ADP是等边三角形, ∴DP=AP= . ……(2分) 如图,过点D作DH⊥x 轴于点H,延长EB交DH于点G, 则BG⊥DH. H G F E x y B A O D P 方法(一) 在Rt△BDG中,∠BGD=900, ∠DBG=600. ∴BG=BD•cos600=×=. DG=BD•sin600=×= . ∴OH=EG=, DH= ∴点D的坐标为( , ) ……(2分) 方法(二) 易得∠AEB=∠BGD=900,∠ABE=∠BDG, ∴△ABE∽△BDG, ∴ 而AE=2, BD=OP= , BE=2, AB=4,则有 ,解得BG= ,DG= ∴OH= , DH= ∴点D的坐标为(, ) ……(2分) (3)假设存在点P, 在它的运动过程中,使△OPD的面积等于 . H G F E x y B A O D P 设点P为(t,0),下面分三种情况讨论: ①当t>0时,如图,BD=OP=t, DG=t, ∴DH=2+t. ∵△OPD的面积等于 , ∴ , 解得 , ( 舍去) . ∴点P1的坐标为 (, 0 ) ②当<t≤0时,如图,BD=OP=-t, BG=-t, x y B A O D P H G F E ∴DH=GF=2-(-t)=2+t. ∵△OPD的面积等于, ∴ , 解得 , . ∴点P2的坐标为(, 0),点P3的坐标为(, 0). ③当t≤ 时,如图,BD=OP=-t, DG=-t, x y B A O D P H G E ∴DH=-t-2. ∵△OPD的面积等于 , ∴ , 解得 (舍去), ∴点P4的坐标为(, 0) 综上所述,点P的坐标分别为P1 (, 0)、P2 ( , 0)、P3 ( , 0) 、 P4 ( , 0) ……(4分)查看更多
相关文章
您可能关注的文档
- 2008年浙江省金华市初中毕业生学业水平考试数学试题卷及参考答案
- 超市社会实践心得体会汇总
- 数学(理)卷·2018届山西省运城市康杰中学高考模拟(一)(2018
- 科学计划总结之八年级科学上册教学总结
- 高考数学专题复习练习第十节 第三节 变量的相关关系
- 2020高考地理二轮优选习题 专题三 大气与水的运动规律 微专题12 常见天气系统学案
- 2018-2019学年安徽省六安市舒城中学高二下学期期末考试物理试题 Word版
- 2020八年级语文上册 第一单元 1 消息二则导学案 新人教版
- 数学文卷·2019届广东省揭阳市普宁华美实验学校高二上学期第一次月考(2017-09)
- 人教版六年级数学下册第3单元检测试卷 (2)