黑龙江省哈三中2020届高三第四次模拟数学（理）试题

黑龙江省哈三中2020届高三第四次模拟数学（理）试题

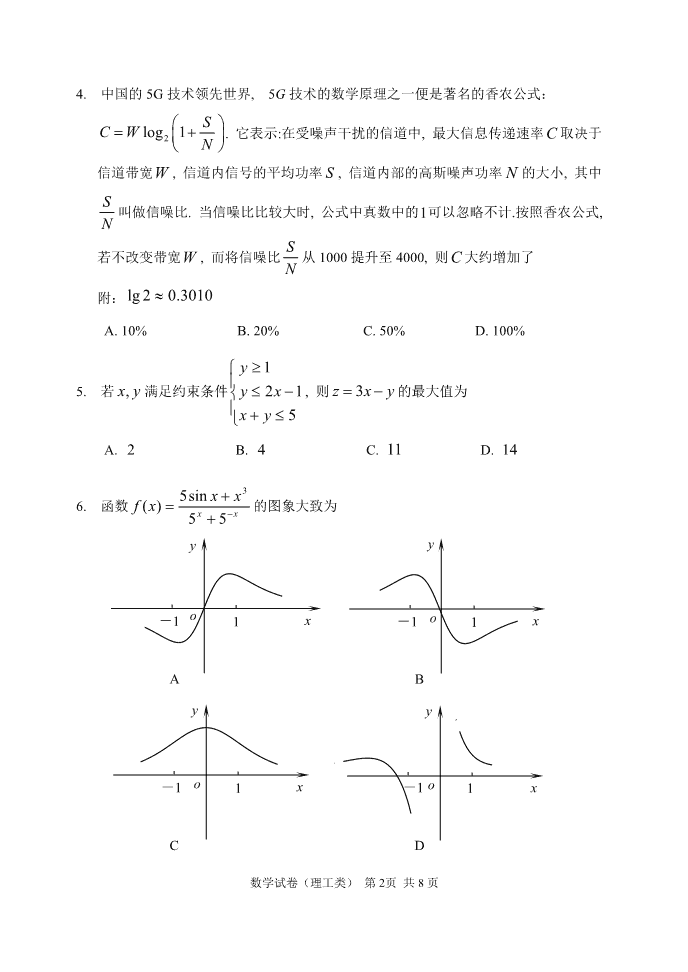
数学试卷（理工类） 第 1页 共 8 页 2020 年高三学年第四次高考模拟考试 数学 试卷（理工类） 考试说明：本试卷分第 I 卷（选择题）和第 II 卷（非选择题）两部分，满分 150 分，考 试时间 120 分钟． （1）答题前，考生先将自己的姓名、准考证号码填写清楚； （2）选择题必须使用 2B 铅笔填涂, 非选择题必须使用 0.5 毫米黑色字迹的签 字笔书写, 字体工整, 字迹清楚； （3）请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案 无效，在草稿纸、试题卷上答题无效； （4）保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀． 第 I 卷 （选择题, 共 60 分） 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只 有一项是符合题目要求的．) 1. 设集合  03  xxA , 集合  022  xxxB , 则  BA A.  2, B.  3, C.  2,1 D.  2,1 2. 复数 z 的共轭复数为 z , 且满足 5 zz , 则复数 z 的模是 A. 1 B. 2 C. 5 D. 5 3. 已知向量 m )2,3( , n ),4( x , 若 m  n, 则 x A. 6 B. 3 8 C. 3 8 D. 6 数学试卷（理工类） 第 2页 共 8 页 4. 中国的 5G 技术领先世界, 5G 技术的数学原理之一便是著名的香农公式： 2log 1 SC W N      . 它表示:在受噪声干扰的信道中, 最大信息传递速率C 取决于 信道带宽W , 信道内信号的平均功率 S , 信道内部的高斯噪声功率 N 的大小, 其中 S N 叫做信噪比. 当信噪比比较大时, 公式中真数中的1可以忽略不计.按照香农公式, 若不改变带宽W , 而将信噪比 S N 从 1000 提升至 4000, 则C 大约增加了 附： 3010.02lg  A. 10% B. 20% C. 50% D. 100% 5. 若 yx, 满足约束条件       5 12 1 yx xy y , 则 yxz  3 的最大值为 A. 2 B. 4 C. 11 D. 14 6. 函数 xx xxxf   55 sin5)( 3 的图象大致为 C D A y o x1－1 o x y 1－1 B o x y 1－1 o x y 1－1 数学试卷（理工类） 第 3页 共 8 页 7. 一个物体做变速直线运动, 在时刻 t 的速度为 2)( 3  ttv ( t 的单位: h, v 的单位: km/h), 那么它在 10  t 这段时间内行驶的路程 s (单位: km)的值为 A. 3 2 B. 4 7 C. 3 5 D. 2 8. 为了得到函数 cos2y x 的图象, 只需把函数 2sin cos6 6y x x             的图象 A. 向右平行移动 12  个单位长度 B. 向左平行移动 12  个单位长度 C. 向左平行移动 6  个单位长度 D. 向右平行移动 6  个单位长度 9. 已知圆 2 2 1 : 0C x y kx y    和圆 2 2 2 : 2 1 0C x y ky    的公共弦所在的直线 恒过定点 M , 且点 M 在直线 2 nymx 上, 则 22 nm  的最小值为 A. 1 5 B. 5 5 C. 2 5 5 D. 4 5 10. 已知正方体 1 1 1 1ABCD A B C D 的外接球的体积为 4 3  , 将正方体割去部分后, 剩余几何体的三视图如图所示, 则剩余几何体的体积为 A. 27 32 B. 27 34 C. 27 316 D. 3 2 正视图 侧视图 俯视图 数学试卷（理工类） 第 4页 共 8 页 11. 若实数 ba, 满足 baba lglg)21lg(2  , 则 ab 的最小值为 A. 2 B. 22 C. 2lg3 D. 2lg 12. 已知函数 12ln2)(  xkxf x , 若 2ln3)( xf 恒成立, 则实数 k 的取值范围是 A.  ,5 B.  ,8 C.  ,10 D.  ,11ln3 第Ⅱ卷 （非选择题, 共 90 分） 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分，将答案填在答题卡相应的位置上．） 13. 若      5 1,3~ BX , 则   12XE . 14. 若锐角 满足 5 3 4cos  ）（  , 则 ）（ 42sin   = . 15. 我国在北宋年间(公元 1084 年)第一次印刷出版了《算经十书》, 即贾宪的《黄帝九 章算法细草》,刘益的《议古根源》, 秦九韶的《数书九章》, 李冶的《测圆海镜》和 《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》, 朱世杰的 《算学启蒙》和《四元玉鉴》．这些书中涉及的很多方面都达到古代数学的高峰, 其 中一些“算法”如开立方和开四次方也是当时世界数学的高峰．哈三中图书馆中正好 有这十本书，现在小张同学从这十本书中任借三本阅读, 那么他借到的三本书中书名 中恰有一个“算”字的概率为 . 16. 经过原点的直线交椭圆 12 2 2 2  b y a x  0 ba 于 ,P Q 两点（点 P 在第一象限）, 若点 P 关于 x 轴的对称点为 M ，且 1 3PA PM   ，直线QA 与椭圆交于点 B ，且满 足 BP PQ ，则直线 BP 和 BQ的斜率之积为 , 椭圆的离心率为 . 数学试卷（理工类） 第 5页 共 8 页 三、解答题（本大题共 6 小题，共 70 分，解答应写出文字说明，证明过程或演算步骤．） 17.（本小题满分 12 分） 已知各项均为正数的数列 na , 其前 n 项和为 nS , 满足 2 2 nn n aaS  . (1) 求数列 na 的通项公式; (2) 若 1 12   nn a n aab n , 求数列 nb 的前 n 项和 nT . 18.（本小题满分 12 分） 如 图 , 四 棱 锥 P ABCD 的 底 面 ABCD 是 矩 形 , 平 面 PAD  平 面 ABCD , 2PA PD  , 且 PA PD , 点 N 为 BC 中点. (1) 证明：平面 PAB  平面 PCD ; (2) 直线 PB 和平面 PAD 所成的角为 45，求二面角 A PN B  的余弦值. N A D P CB 数学试卷（理工类） 第 6页 共 8 页 19. （本小题满分 12 分） 已知某种新型病毒的传染能力很强, 给人们生产和生活带来很大的影响, 所以创新 研发疫苗成了当务之急．为此, 某药企加大了研发投入, 市场上这种新型冠状病毒的 疫苗 A 的研发费用 x （百万元）和销量 y （万盒）的统计数据如下： 研发费用 x （百万元） 2 3 6 10 13 14 销量 y （万盒） 1 1 2 2.5 4 4.5 （1）根据上表中数据, 建立 y 关于 x 的线性回归方程 axby ˆˆˆ  （用分数表示）; （2）根据所求的回归方程, 估计当研发费用为1600万元时, 销售量为多少？ 参考公式： 1 2 1 ( )( ) ( ) ˆ n i i i n i i x x y y b x x                n i i n i ii xnx yxnyx 1 22 1 , xbya ˆˆ  . 数学试卷（理工类） 第 7页 共 8 页 20．（本小题满分 12 分） 已知圆 M 经过点  0,1 且与直线 1y   相切, 圆心 M 的轨迹为曲线 C , 过点  0,2N 做直线与曲线 C 交于不同两点 ,A B , 三角形OAB 的垂心为点 H . (1) 求曲线C 的方程; (2) 求证：点 H 在一条定直线上，并求出这条直线的方程. 21. 已知函数 axxf x  e)( 的图象与直线 xy )1(e2  2e 相切. (1) 求实数 a 的值; (2) 若存在实数 k 满足 0)( kf 且 0)1( kf , 求证: )1ln(e kkxx  . 数学试卷（理工类） 第 8页 共 8 页 请考生在第 22、23 二题中任选一题作答，如果多做，则按所做的第一题记分. 22. （本小题满分 10 分）[4-4:极坐标与参数方程] 在直角坐标系中, 直线l 的参数方程为        ty t,x 2 1 2 33 （ t 为参数）, 以坐标 原点为极点, x 轴的正半轴为极轴建立极坐标系, 曲线C 的极坐标方程为  sin4 ,若直线l 与曲线C 交于 BA, 两点. (1) 若 )0,3(P ，求 PBPA  ; (2) 若点 M 是曲线C 上不同于 BA, 的动点，求 MAB 面积的最大值. 23. （本小题满分 10 分）[4-5:不等式选讲] 已知函数 kxxf  3)( , 1)( xf 的解集为     3 11 xx . (1) 若存在 x , 使 axxf  13)( 成立, 求实数 a 的取值范围; (2) 如果对于 yx, 满足 412  yx , 13 7  y , 求证: 9)( xf .