专题08+函数与方程(题型专练)-2019年高考数学(理)热点题型和提分秘籍
1.已知函数f(x)=lnx-x-2的零点为x0,则x0所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
【答案】C
2.方程|x2-2x|=a2+1(a>0)的解的个数是( )
A.1 B.2
C. 3 D.4
【解析】(数形结合法)
∵a>0,∴a2+1>1.
而y=|x2-2x|的图象如图,
∴y=|x2-2x|的图象与y=a2+1的图象总有两个交点.
【答案】B
3.已知函数f(x)=ex+x,g(x)=lnx+x,h(x)=lnx-1的零点依次为a,b,c,则( )
A.a
0,
∴01,故选A.
【答案】A
4.已知函数f(x)=()x-cosx,则f(x)在[0,2π]上的零点个数为( )
A.1 B.2
C.3 D.4
【解析】函数f(x)=()x-cosx的零点个数为()x-cosx=0⇒()x=cosx的根的个数,即函数h(x)=()x与g(x)=cosx的图象的交点个数,如图所示,在区间[0,2π]上交点个数为3,故选C.
【答案】C
5.设定义在R上的函数f(x)是最小正周期为2π的偶函数,f′(x)是f(x)的导函数,当x∈[0,π]时,00,则函数y=f(x)-sinx在[-2π,2π]上的零点个数为( )
A.2 B.4
C.5 D.8
【答案】B
6.函数f(x)=-cosx在[0,+∞)内( )
A.没有零点 B.有且仅有一个零点
C.有且仅有两个零点 D.有无穷多个零点
【解析】原函数f(x)=-cosx可理解为幂函数x与余弦函数的差,其中幂函数在区间[0,+∞)上单调递增、余弦函数的最大值为1,在同一坐标系内构建两个函数的图象,注意到余弦从左到右的第2个最高点是x=2π,且>1=cos2π,不难发现交点仅有一个.正确选项为B.
【答案】B
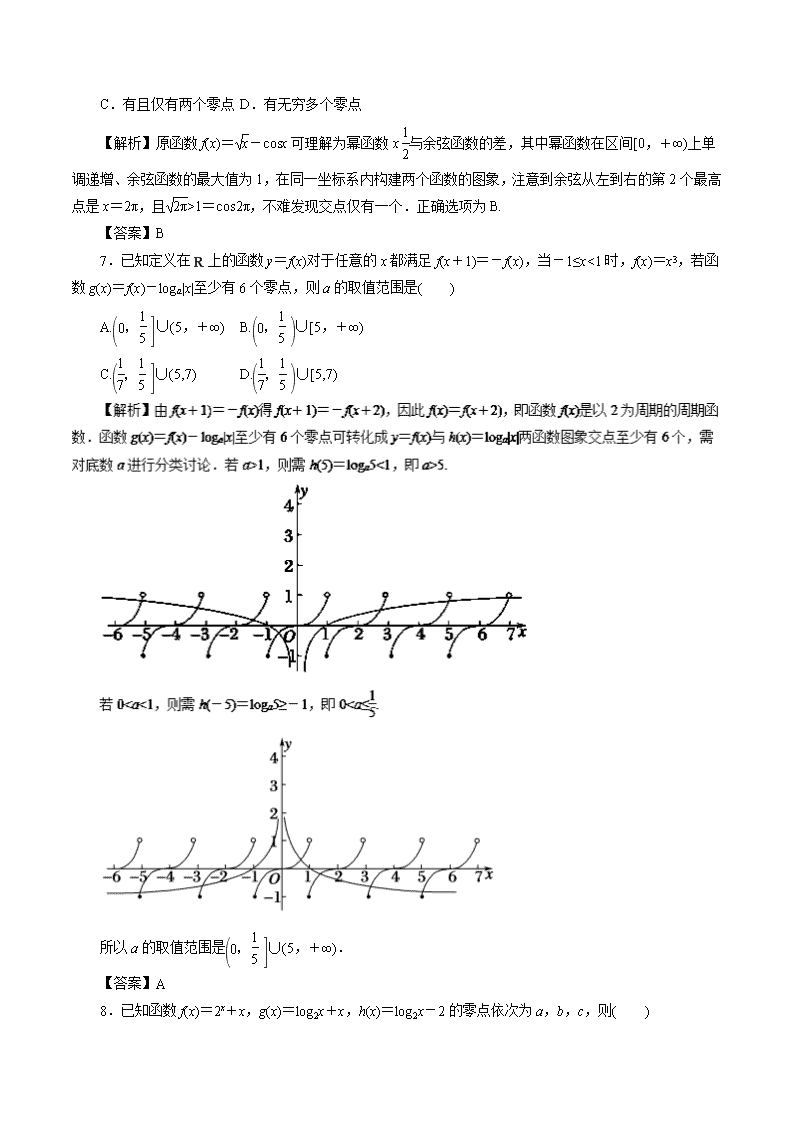
7.已知定义在R上的函数y=f(x)对于任意的x都满足f(x+1)=-f(x),当-1≤x<1时,f(x)=x3,若函数g(x)=f(x)-loga|x|至少有6个零点,则a的取值范围是( )
A.∪(5,+∞) B.∪[5,+∞)
C.∪(5,7) D.∪[5,7)
所以a的取值范围是∪(5,+∞).
【答案】A
8.已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log2x-2的零点依次为a,b,c,则( )
A.a0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
【解析】设g(x)=,由于函数g(x)==-在(1,+∞)上单调递增,函数h(x)=2x在(1,+∞)上单调递增,故函数f(x)=h(x)+g(x)在(1,+∞)上单调递增,所以函数f(x)在(1,+∞)上只有唯一的零点x0,且在(1,x0)上f(x1)<0,在(x0,+∞)上f(x2)>0,故选B.
【答案】B
11.函数f(x)=xcos2x在区间[0,2π]上的零点的个数为( )
A.2 B.3
C.4 D.5
【解析】借助余弦函数的图象求解。f(x)=xcos2x=0⇒x=0或cos2x=0,又cos2x=0在[0,2π]上有,,,,共4个根,故原函数有5个零点。故选D。
【答案】D
12.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x。则函数g(x)=f(x)-x+3的零点的集合为( )
A.{1,3} B.{-3,-1,1,3}
C.{2-,1,3} D.{-2-,1,3}
【答案】D
13.若f(x)是奇函数,且x0是y=f(x)+ex的一个零点,则-x0一定是下列哪个函数的零点( )
A.y=f(-x)ex-1 B.y=f(x)e-x+1
C.y=exf(x)-1 D.y=exf(x)+1
【解析】由已知可得f(x0)=-ex0,e-x0f(-x0)=1,故-x0一定是y=exf(x)-1的零点。故选C。
【答案】C
14.某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是( )
A.16小时 B.20小时
C.24小时 D.28小时
【解析】由已知条件,得192=eb,
又48=e22k+b=eb·(e11k)2,
∴e11k===.
设该食品在33 ℃的保鲜时间是t小时,
则t=e33k+b=192 e33k=192(e11k)3=192×=24.
【答案】C
15.已知函数f(x)=则函数f(x)的零点为( )
A.,0 B.-2,0 C. D.0
【答案】D
16.已知[x]表示不超过实数x的最大整数,g(x)=[x]为取整函数,x0是函数f(x)=ln x-的零点,则g(x0)等于( )
A.1 B.2 C.3 D.4
【解析】当x>0时,f′(x)=+>0,则f(x)为(0,+∞)上的增函数,又f(2)=ln 2-1<0,f(e)=ln e-=1->0,所以函数f(x)=ln x-的零点x0满足2a),函数g(x)=f(x)-b有两个零点,即函数y=f(x)的图象与直线y=b有两个交点,结合图象可得a<0或φ(a)>h(a),即a<0或a3>a2,解得a<0或a>1,故a∈(-∞,0)∪
(1,+∞)。
【答案】(-∞,0)∪(1,+∞)
22.已知关于x的方程x2+mx-6=0的一个根比2大,另一个根比2小,则实数m的取值范围是________。
【解析】设函数f(x)=x2+mx-6,则根据条件有f(2)<0,即4+2m-6<0,解得m<1。
【答案】(-∞,1)
23.已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点的个数为________.
【解析】当0≤x<2时,令f(x)=x3-x=0.
得x=0或x=1,∵f(x+2)=f(x),
∴y=f(x)在[0,6)上有6个零点.
又f(6)=f(3×2)=f(0)=0.
∴f(x)在[0,6]上与x轴的交点个数为7.
【答案】7
24.函数f(x)=ax+1-2a在区间(-1,1)上存在一个零点,则实数a的取值范围是________.
【解析】当a=0时,函数f(x)=1在(-1,1)上没有零点,所以a≠0.根据零点存在性定理可得f(-1)f(1)<0,即(-3a+1)·(1-a)<0,所以(a-1)(3a-1)<0,解得,∴k>时,函数y=f(x)-kx在(-∞,0)上有一个零点;当x>0时,f(x)=ln(x+1),f′(x)=∈(0,1),要使函数y=f(x)-kx在(0,+∞)上有一个零点,则0
查看更多