- 2024-01-01 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年安徽省六安市舒城中学高二下学期第一次统考(开学考试)数学(理)试题(解析版)
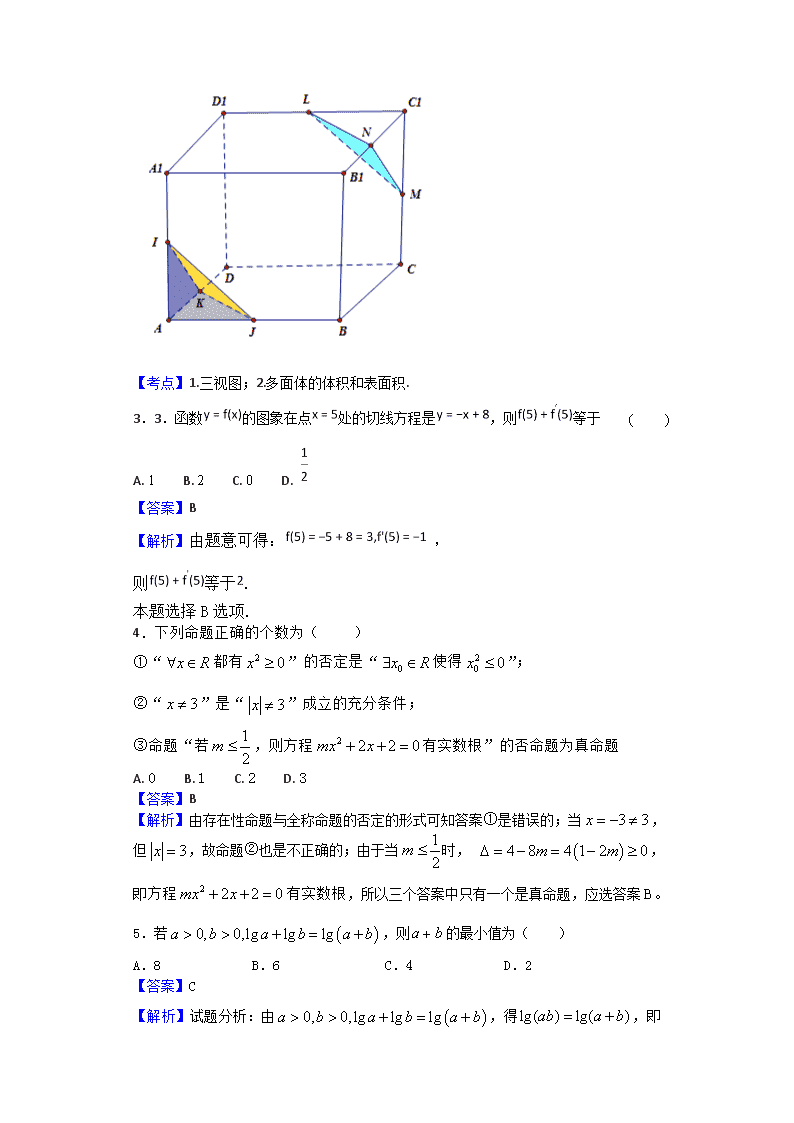
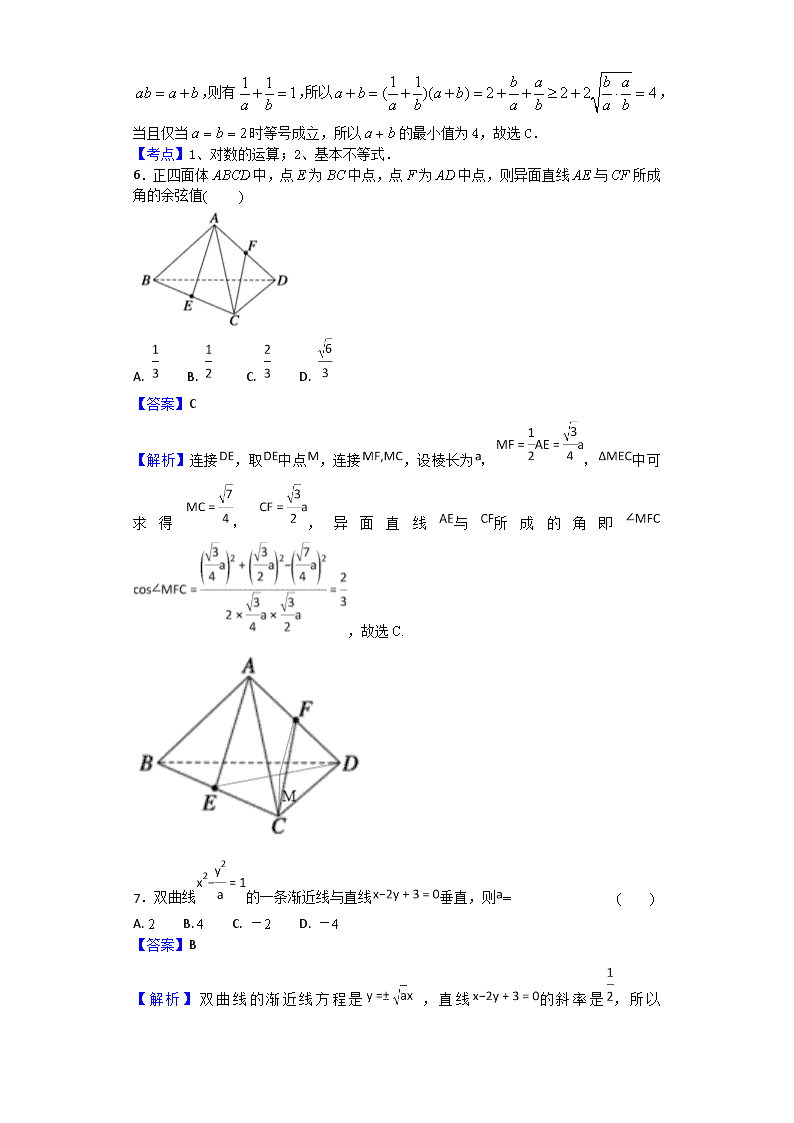
2017-2018学年安徽省六安市舒城中学高二下学期第一次统考(开学考试)数学(理)试题 一、单选题 1.已知分别是定义在上的偶函数和奇函数,且 ,则 ( ) A. -3 B. -1 C. 1 D. 3 【答案】C 【解析】,故选C. 2.一个多面体的三视图如图所示,则该多面体的表面积为 ( ) A. B. C. D. 【答案】A 【解析】试题分析:如图,几何体为棱长为2的正方体切下如图所示的两个三棱锥,切下的小三棱锥的侧棱长为1,所以该多面体的表面积为,故选C. 【考点】1.三视图;2.多面体的体积和表面积. 3.3.函数的图象在点处的切线方程是,则等于 ( ) A. 1 B. 2 C. 0 D. 【答案】B 【解析】由题意可得: , 则等于. 本题选择B选项. 4.下列命题正确的个数为( ) ①“都有”的否定是“使得”; ②“”是“”成立的充分条件; ③命题“若,则方程有实数根”的否命题为真命题 A. 0 B. 1 C. 2 D. 3 【答案】B 【解析】由存在性命题与全称命题的否定的形式可知答案①是错误的;当,但,故命题②也是不正确的;由于当时, ,即方程有实数根,所以三个答案中只有一个是真命题,应选答案B。 5.若,则的最小值为( ) A.8 B.6 C.4 D.2 【答案】C 【解析】试题分析:由,得,即 ,则有,所以,当且仅当时等号成立,所以的最小值为4,故选C. 【考点】1、对数的运算;2、基本不等式. 6.正四面体ABCD中,点E为BC中点,点F为AD中点,则异面直线AE与CF所成角的余弦值( ) A. B. C. D. 【答案】C 【解析】连接,取中点,连接,设棱长为,,中可求得,,异面直线与所成的角即 ,故选C. 7.双曲线的一条渐近线与直线垂直,则= ( ) A. 2 B. 4 C. -2 D. -4 【答案】B 【解析】双曲线的渐近线方程是 ,直线的斜率是,所以 ,解得,故选B. 8.已知点在椭圆上,点为椭圆的右焦点,的最大值与最小值的比为2,则这个椭圆的离心率为 ( ) A. B. C. D. 【答案】B 【解析】的最大值是,的最小值是,所以 ,即,故选B. 9.已知点是直线上一动点,是圆的两条切线,是切点.若四边形的最小面积是2,则的值为( ) A. B. C. D.2 【答案】D 【解析】试题分析:如图所示,根据对称性可知,当取得最小值时面积取得最小值,而,所以当最短时,最小,即时最小,此时,四边形的面积为,解得. 【考点】直线与圆的位置关系. 【思路点晴】本题主要考查直线与圆的位置关系. 涉及比较多的知识点,一是连接圆心和切点的直径和切线垂直;二是根据对称性,将四边形的面积转化为两个直角三角形面积的和;三是最值问题,用化归与转化的数学思想方法转化为点到直线距离的距离来求解.四是点到直线的距离公式,还有圆的一般方程配成标准方程得到圆心和半径. 10.直线过抛物线的焦点,且交抛物线于两点,交其准线于点,已知,则 ( ) A. B. C. D. 4 【答案】C 【解析】 过分别做准线的垂线交准线于两点,设 ,根据抛物线的性质可知,,根据平行线段比例可知,即,解得 ,又,即 ,解得,故选C. 【点睛】抛物线的定义在解题中的应用,当已知曲线是抛物线时,可利用抛物线上的点满足定义,点到焦点的距离转化点为到准线的距离,这样可利用三角形相似或是平行线段比例关系可求得距离弦长以及相关的最值等问题 11.已知边长为的菱形中,,沿对角线折成二面角为的四面体,则四面体的外接球的表面积为( ) A. B. C. D. 【答案】D 【解析】试题分析:如图所示,设两三角形外心分别为,球心为,,故,球的半径为,故球的表面积为. 【考点】几何体外接球. 二、填空题 12.已知方程表示焦点在轴上的椭圆,则的取值范围是____________. 【答案】1查看更多
相关文章
您可能关注的文档
- 2017-2018学年安徽省六安市舒城中学高二下学期第一次统考(开学考试)数学(理)试题(解析版)
- 2019-2020学年江西省新余一中高一(下)摸底生物试卷
- 精品呼唤物业管理进社区征文——渴望有人管
- 甘肃省武威第六中学2020届高三下学期诊断考试英语试题
- 高中物理 第十二章 机械波 2 波的图象课前预习素材 新人教版选修3-4(通用)
- 2017-2018学年四川省宜宾市南溪区第二中学校高二10月月考物理试题 缺答案
- 2018-2019学年河北省承德市第一中学高二下学期第三次月考化学试题 解析版
- 村委会工作自我鉴定
- 专题02+力与直线运动(仿真押题)-2018年高考物理命题猜想与仿真押题
- 2020个人上半年工作总结开头