中考数学全程复习方略第二十三讲直角三角形的边角关系课件
第二十三讲
直角三角形的边角关系
考点一 三角函数的定义
【
主干必备
】
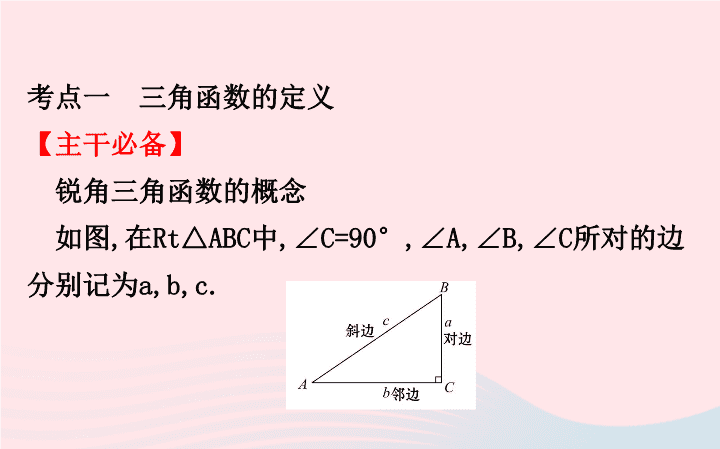
锐角三角函数的概念
如图
,
在
Rt△ABC
中
,∠C=90°,∠A,∠B,∠C
所对的边分别记为
a,b,c.
1.
正弦
:sin A=
=___.
2.
余弦
:cos A=
=___.
3.
正切
:tan A=
=___.
锐角
A
的正弦、余弦、正切统称∠
A
的锐角三角函数
.
【
微点警示
】
(1)
注意自变量
:
锐角三角函数的自变量是角度
,
其取值范围是
:0°<α<90°.
(2)
注意锐角三角函数的值
:
当∠
A
为锐角时
,0
0.
【
核心突破
】
例
1(2019·
甘肃中考
)
在
Rt△ABC
中
,∠C=90°,
tan A= ,
则
cos B=___.
【
明
·
技法
】
根据定义求三角函数值的方法
(1)
分清直角三角形中的斜边与直角边
.
(2)
正确地表示出直角三角形的三边长
,
常设某条直角边长为
k(
有时也可以设为
1),
在求三角函数值的过程中约去
k.
(3)
正确应用勾股定理求第三条边长
.
(4)
应用锐角三角函数定义
,
求出三角函数值
.
(5)
求一个角的三角函数值时
,
若不易直接求出
,
也可把这个角转化成和它相等且位于直角三角形中的角
.
【
题组过关
】
1.(
概念应用题
)
如图
,
在
Rt△ABC
中
,∠ACB=90°,AB⊥CD
于点
D,
下
列各组线段的比不能表示
sin∠BCD
的是
(
)
C
2.(2019·
宜昌中考
)
如图
,
在
5×4
的正
方形网格中
,
每个小正方形的边长都是
1,△ABC
的顶点都在这些小正方形的
顶点上
,
则
sin∠BAC
的值为世纪金榜导学号
(
)
D
3.(2019·
眉山中考
)
如图
,
在
Rt△ABC
中
,∠B=90°,AB=5,BC=12,
将△
ABC
绕
点
A
逆时针旋转得到△
ADE,
使得点
D
落
在
AC
上
,
则
tan∠ECD
的值为
___.
世纪金榜导学号
4.
如图
,
在平面直角坐标系中
,
直线
OA
过点
(2,1),
则
tan α
的值是
___.
世纪金榜导学号
考点二 特殊角的三角函数值
【
主干必备
】
特殊角的三角函数值
α
30°
45°
60°
sin α
___
___
___
α
30°
45°
60°
cos α
___
___
___
tan α
___
___
___
1
【
微点警示
】
(1)
互余两角三角函数之间的关系
:
由上表可得
,
当两角互余时
,
一角的正弦值等于另一个角的余弦值
,
即当∠
A+∠B=90°
时
,
则
sin A=cos B,cos A=sin B.
(2)
锐角三角函数值的变化规律
:
在锐角范围内
,
sin α
、
tan α
的值随
α
的增大而增大
,cos α
的值随
α
的增大而减小
.
【
核心突破
】
例
2
【
原型题
】
(2018·
青海中考
)
在△
ABC
中
,
若
=0,
则∠
C
的度数是
___________.
90°
【
变形题
1】
(
变换条件
)
在△
ABC
中
,
若
=0,
则∠
C
的度数是
___________.
【
变形题
2】
(
变换结论
)
在△
ABC
中
,
若
=0,
则 的值为
________.
90°
1
【
明
·
技法
】
熟记特殊角的三角函数值的两种方法
(1)
按值的变化
:30°,45°,60°
角的正余弦的分母都
是
2,
正弦的分子分别是
1, , ,
余弦的分子分别是
, ,1,
正切分别是
,1, .
(2)
特殊值法
:
①
在直角三角形中
,
设
30°
角所对的直角边为
1,
那么三
边长分别为
1, ,2;
②
在直角三角形中
,
设
45°
角所对的直角边为
1,
那么
三边长分别为
1,1, .
【
题组过关
】
1.(2019·
天津中考
)2sin 60°
的值等于
(
)
A.1 B. C. D.2
C
2.
当∠
A
为锐角
,
且
查看更多