小学数学精讲教案5_1_2_2 乘除法数字谜（一） 教师版

小学数学精讲教案5_1_2_2 乘除法数字谜（一） 教师版

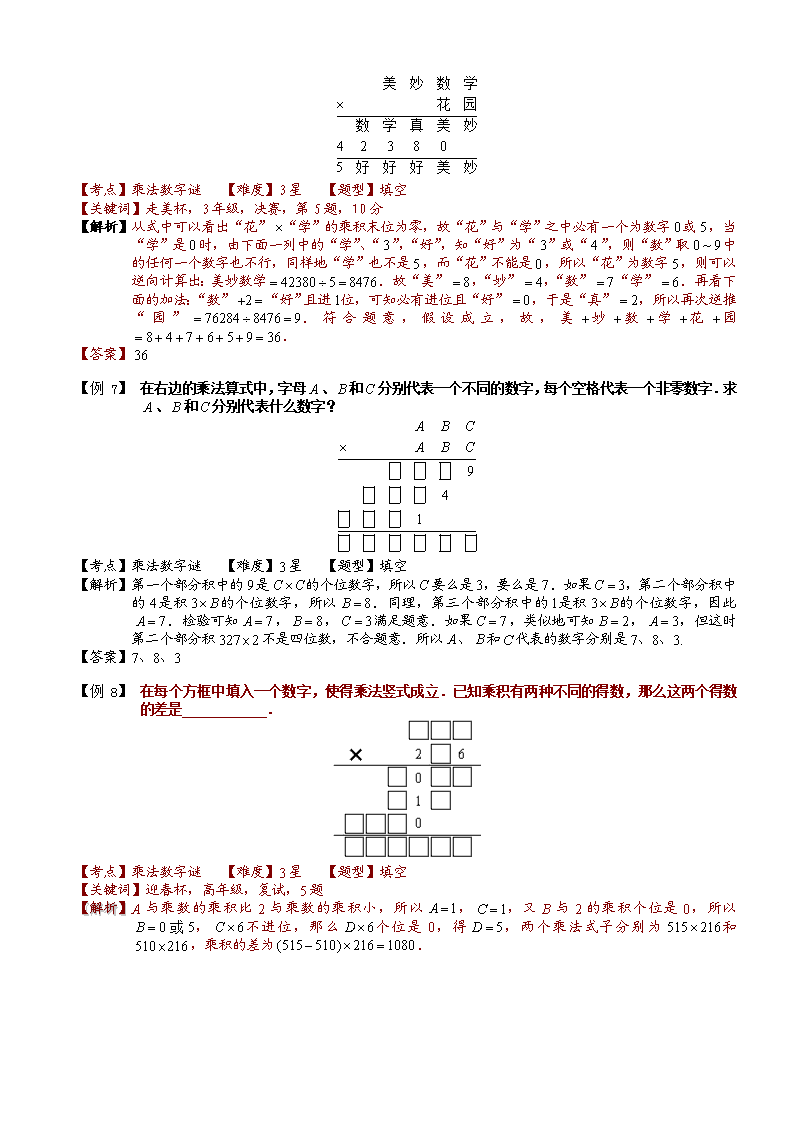
‎5-1-2-2.乘除法数字谜（一）‎ 教学目标 数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突破口来解决问题．最后通过例题的学习，总结解数字谜问题的关键是找到合适的解题突破口．在确定各数位上的数字时，首先要对填写的数字进行估算，这样可以缩小取值范围，然后再逐一检验，去掉不符合题意的取值，直到取得正确的解答． ‎ 知识点拨 1. 数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．‎ 2. 数字谜突破口：这种不完整的算式，就像“谜”一样，要解开这样的谜，就得根据有关的运算法则，数的性质（和差积商的位数，数的整除性，奇偶性，尾数规律等）来进行正确的推理，判断．‎ 3. 解数字谜：一般是从某个数的首位或末位数字上寻找突破口．推理时应注意：‎ ‎⑴ 数字谜中的文字，字母或其它符号，只取中的某个数字；‎ ‎⑵ 要认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件；‎ ‎⑶ 必要时应采用枚举和筛选相结合的方法（试验法），逐步淘汰掉那些不符合题意的数字；‎ ‎⑷ 数字谜解出之后，最好验算一遍．‎ 例题精讲 模块一、乘法数字谜 【例 1】 下面是一个乘法算式：问：当乘积最大时，所填的四个数字的和是多少？‎ ‎【考点】乘法数字谜 【难度】1星 【题型】填空 ‎【关键词】华杯赛，初赛，第2题 【解析】 乘积是两位数并且是5的倍数，因而最大是95.95÷5＝19，所以题中的算式实际上是 所以，所填四个数字之和便是1＋9＋9＋5＝24‎ ‎【答案】‎ 【例 1】 下面两个算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字．，。___________‎ ‎【考点】乘法数字谜 【难度】2星 【题型】填空 ‎ ‎【关键词】走美杯，四年级，初赛，第12题，五年级，初赛，第11题 【解析】 由知，“美”不为1，且“美”ד妙”<10，如果“美”为2，根据“美”ד学”的个位数为“妙”，那么“妙”为偶数，即为4，推出“学”为7，又由 “美”+“学”=“数”，可知“数”为9，所以2497。‎ ‎【答案】‎ 【例 2】 北京有一家餐馆，店号“天然居”，里面有一副著名对联：客上天然居，居然天上客。巧的很，这副对联恰好能构成一个乘法算式(见右上式)。相同的汉字代表相同的数字，不同的汉字代表不同的数字。“天然居”表示成三位数是_______。‎ ‎【考点】乘法数字谜 【难度】2星 【题型】填空 ‎【关键词】走美杯，4年级，决赛，第6题，10分 【解析】 因为竖式中五位数乘4仍是五位数，所以“客”是人于0小于3的偶数，只能是2，并推知“居”8。因为“上”乘4不向上进位，且是奇数，所以“上”1，并推知“然”7。则所表示的三位数是978。‎ ‎【答案】‎ 【例 3】 下面算式(1)是一个残缺的乘法竖式，其中□≠2，那么乘积是多少？‎ ‎ ‎ ‎【考点】乘法数字谜 【难度】2星 【题型】填空 ‎ 【解析】 如式(2)，由题意a≠2，所以b≥6，从而d≥6．由22□÷c≥60和c＞2知c=3，所以22□是225或228，或76．因为75×399＜30 000，所以．再由乘积不小于30000和所有的□≠2，推出唯一的解76×396=30096．‎ ‎【答案】76×396=30096‎ 【例 4】 下面残缺的算式中，只写出了3个数字1，其余的数字都不是1，那么这个算式的乘积是？‎ ‎ ‎ ‎【考点】乘法数字谜 【难度】2星 【题型】填空 ‎ 【解析】 为了说明的方便，这个算式中的关键数字用英文字母表示．很明显e= 0．从的个位数是1，b可能是3，7，9三数之一，两位数应是（100+f）的因数．101，103，107，109是质数，f=0或5也明显不行．102=17×6，则=17，C只能取3，，不是三位数；104=13×8,则，c可取7，c ×=7×13，仍不是三位数；106=53×2，，c=7，是三位数；108=27×4，则=27，c是3．，不是三位数．‎ 因此这个乘法算式是53×72=3816，故这个算式的乘积是3816。‎ ‎【答案】3816‎ 【例 5】 右面的算式中，每个汉字代表一个数字（0~9），不同汉字代表不同数字．美+妙+数+学+花+园= ． ‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎【关键词】走美杯，3年级，决赛，第5题，10分 【解析】 从式中可以看出“花”“学”的乘积末位为零，故“花”与“学”之中必有一个为数字或，当“学”是时，由下面一列中的“学”、“”，“好”，知“好”为“”或“”，则“数”取中的任何一个数字也不行，同样地“学”也不是，而“花”不能是，所以“花”为数字，则可以逆向计算出：美妙数学．故“美”，“妙”，“数”“学”．再看下面的加法：“数”“好”且进位，可知必有进位且“好”，于是“真”，所以再次逆推“园”．符合题意，假设成立，故，美妙数学花园．‎ ‎【答案】‎ 【例 1】 在右边的乘法算式中，字母、和分别代表一个不同的数字，每个空格代表一个非零数字．求、和分别代表什么数字？‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎ 【解析】 第一个部分积中的是的个位数字，所以要么是，要么是．如果，第二个部分积中的是积的个位数字，所以．同理，第三个部分积中的是积的个位数字，因此．检验可知，，满足题意．如果，类似地可知，，但这时第二个部分积不是四位数，不合题意．所以、和代表的数字分别是7、8、3.‎ ‎【答案】7、8、3‎ 【例 2】 在每个方框中填入一个数字，使得乘法竖式成立．已知乘积有两种不同的得数，那么这两个得数的差是 ．‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎【关键词】迎春杯，高年级，复试，5题 【解析】 A与乘数的乘积比2与乘数的乘积小，所以，，又B与2的乘积个位是0，所以，不进位，那么个位是0，得，两个乘法式子分别为和，乘积的差为．‎ ‎【答案】‎ 【例 1】 在图中的每个方框中填入一个适当的数字，使得乘法竖式成立。乘积等于 。‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎【关键词】走美杯，5年级，决赛，第6题，10分 【解析】 根据乘法算式，被乘数乘以后得到一个位数，且此三位数的最高位在最终的运算中进位了，所以被乘数的最高位应该是，而乘数的十位数乘以被乘数后得到的结果也是三位数，所以乘数的十位数只能是或，如果是，那么被乘数的十位数肯定是，第三位数字必为，但此时不可能是位数，故乘数第二位必为，被乘数第三位必为，被乘数第二位为或，假设被乘数第二位是，则不可能是六位数，所以被乘数必然是，经试算，乘式为。‎ ‎【答案】‎ 【例 2】 如图，请在右图每个方框中填入一个数字，使乘法竖式成立。‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎【关键词】走美杯，初赛，六年级，第7题 【解析】 ‎【答案】‎ 【例 1】 在下面的乘法算式中，相同的字母表示相同的数字，不同的字母表示不同的数字．则 ，表示的五位数是 ．‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎ ‎【关键词】学而思杯，5年级，第13题 【解析】 ‎,‎ ‎【答案】,‎ 【例 2】 如图，请在右图每个方框中填入一个不是8的数字，使乘法竖式成立。‎ ‎8‎ ‎8‎ ‎8‎ ‎8‎ ‎8‎ ‎×‎ ‎【考点】乘法数字谜 【难度】4星 【题型】填空 ‎ ‎【关键词】走美杯，四年级，第11题 【解析】 ‎【答案】‎ 【例 1】 在下面的算式中：，别代表0～9中的三个不同的数字，那么，数字是　　　．‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎ ‎【关键词】迎春杯，中年级，复试，第8题 【解析】 这是一道数字谜问题．考察同学们的推理能力．首先列成竖式：‎  从，及乘积为看，，所以．‎ 从竖式的十位上看，的个位数字是0．‎ ‎（1）当时，从十位看，的个位数字必是0，只能是，是偶数或，为偶数．‎ ‎①若，是偶数．从及乘积看，，因为且是偶数，所以时是无解的． ‎②若，为偶数．从算式的千位看，由于，由于不能进位，所以7加几也不能等于1．所以时是无解的． ‎（2）当时，从百位看，的个位数字必是9，十位数字必是0，那么．此时． ‎【答案】301‎ 【例 1】 如图所示的乘法竖式中，“学而思杯”分别代表0～9 中的一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么“学而思杯”代表的数字分别为________‎ ‎【考点】乘法数字谜 【难度】3星 【题型】填空 ‎ 【解析】 首先从式子中可以看出“思”，另外第三个部分积的首位只能为9，所以“学”只能为3．由于3个部分积都是四位数，而且第三个部分积的首位为9，所以它比其它两个部分积要大，从而“学”比“而”和“杯”都大，所以“而”和“杯”只能分别为1和2，这样“学而思杯”就可能为3102或3201．分别进行检验，发现，与算式不相符，而符合，所以“学而思杯”代表的数字分别为3、2、0、1．‎ ‎【答案】3、2、0、1‎ 模块二、除法数字谜 【例 2】 在方格内填上适当的数字，使得除法竖式成立。‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 ‎【关键词】走美杯，决赛，5年级，决赛，第9题，10分 【解析】 ‎20047-13=200342×3×7×53。由商的个位是2知，除数乘以2的个位是4，所以除数的个位是2或7。因为20034只有一个因子2，所以20034只能分解成一个偶数与一个奇数的乘积，由商是偶数推知除数是奇数，所以除数的个位是7。20034的两位数因数中只有3=27符合要求，所以除数是27，商是20034÷27742。‎ ‎【答案】‎ 【例 3】 如图所示的除法算式中，每个各代表一个数字，则被除数是 。 ‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 ‎【关键词】希望杯，4年级，初赛，8题 【解析】 先确定商首位是8，再估量出除数首位是5，确定商的末位1，得到被除数为4620.‎ ‎【答案】‎ 【例 1】 右边的除法算式中，商数是 。‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 ‎【关键词】希望杯，五年级，初赛，第11题，4分 【解析】 除数的百位是6，积是一个三位数，所以商的十位一定是1,除数的个位是7，被除数个位是1，所以商的个位是3，所以商是3‎ ‎【答案】‎ 【例 2】 右面算式中的每个“奇”字代表1、3、5、7、9中的一个，每个“偶”字代表0、2、4、6、8中的一个，为使算式成立，求出它们所代表的值。‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 【关键词】奇偶分析法 【解析】 为了叙述方便，把算式中每个“奇”与“偶”字都标上角码，如下式所示。‎ 由于因此所在位必定向“奇2”所在位借1，因而排除“偶4”=0。又由于，所以 ‎①若，则，，，，而 ‎（积为奇奇偶），22×8=176（积为奇奇偶）因此，若24×6=144（积为奇偶偶），24×8=192（积为奇奇偶），于是，。而的差不可能等于4，因此，42×4=168（积为奇偶偶），42×6＝252（积为偶奇偶），42×8=336（积为奇奇偶），于是，因为，所以有，便得：‎ ‎　　 44×4＝176 （积为奇奇偶）；44×6=264 （积为偶偶偶）；44×8＝352 （积为奇奇偶），因此 ‎ ②若，则，而22×6=132（积为奇奇偶），22×8＝176（积为奇奇偶），“偶2”≠4。‎ ‎【答案】1764÷42＝42‎ 【例 1】 在右图的每个方框中填入一个数字，使得除法算式成立．则被除数应是___________．‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 ‎【关键词】迎春杯，五年级，初赛，第11题 【解析】 如下图，我们将空格标上字母，以便分析，‎ 由，得．因为，可以得知或者6．‎ ‎⑴如果，则没有进位，所得个位必是偶数，那么，必是奇数．因为， 所以，可能是1、3、5、7、9，其中只有18可以表示成两个一位数的乘积，．所以可能是1．如果，得，那么，．只能是，，，，而最大为189，这样将为0．不符题意．所以不成立．‎ ‎⑵如果，分别将1至9代入X进行计算，可以发现，当、2、3、7、8时，第一次除法后得到的余数都大于除数，所以可以排除；‎ ‎①若，得，，进而得到，，，因为 的结果是一个两位数，所以或者2．当的时候，，而 没有借位，所以结果最大为5，产生矛盾，故，进而推出，，，符合题目要求，被除数为38686；‎ ‎②若，由第一次除法可以推出，只能是6或者7，但是无论 还是7，都无法满足，所以排除；‎ ‎③若，由第一次除法可以推出，只能是8或者9，但是无论 还是7，都无法满足，所以排除；‎ ‎④若，由第一次除法可以推出，那么，但是不存在能使这个等式成立的整数，所以可以排除；‎ 综上所述，只有，的时候满足题目中的除式，所以被除数为38686．‎ ‎【答案】‎ 【例 1】 在方框中填入适当的数字，使得除法竖式成立．已知商为奇数，那么除数为 ：‎ ‎ ‎ ‎【考点】除法数字谜 【难度】3星 【题型】填空 ‎ ‎【关键词】迎春杯，高年级，决赛，2题 【解析】 先看除式的第二、三行，一个三位数减去一个两位数，得到一个一位数，可得这个三位数的前两位为1、0，这个两位数的十位数字为9，个位不能为0．除数是一个三位数，它与商的百位和个位相乘，所得的两个三位数的百位都是9，那么可得商的百位和个位相同．先将已得出的信息填入方框中，并用字母来表示一些方框中的数，如右图所示．由于商为奇数，所以是奇数，可能为1、3、7、9(不可能为5)．若为1，则，而为三位数，于是，又这个乘积的十位数字为0，而不能为0，矛盾．所以不为1；若为3，则，可能为1、4、7， 相应的为304、314、324．当为314和324时所的结果的十位数字不可能为0，不合题意；若为304，则可能为1或2，经检验为1和2时都与竖式不符，所以也不能为3；若为7，则，只有时满足，此时，那么．经检验满足题意；若为9，则，只能为7，此时，则只能为1．经检验也不合题意．所以只有除数为136时竖式成立，所以所求的除数即为136． ‎ ‎【答案】136‎ 【例 2】 右图是一个分数等式：等式中的汉字代表数字1、2、3、4、5、6、7、8和9，不同的汉字代表不同的数字，如果“北”和“京”分别代表1和9，请写出“奥运会”所代表的所有三位整数，并且说明理由。‎ ‎【考点】除法数字谜 【难度】6星 【题型】填空 ‎【关键词】华杯赛，决赛，第14题，10分 【解析】 ‎① ∴9×奥运会=梦想成真，∴梦想成真为9的倍数 于是：“梦”＋“想”＋“成”＋“真”为9的倍数 而：“梦”＋“想”＋“成”＋“真” 最大为：8＋7＋6＋5=26‎ 最小为：2＋3＋4＋5=14‎ 所以：“梦”＋“想”＋“成”＋“真” 在14至26之间，且为9的倍数，推出：“梦”＋“想”＋“成”＋“真”=18‎ ‎②“奥”、“运”、“会”、“梦”、“想”、“成”、“真”分别代表2—8‎ 所以：“奥”＋ “运”＋“会”=2＋3＋…＋8-18=17‎ 可以得出：“奥”、“运”、“会”必是下面三组中的一组： 8、7、2 ; 8、6、3 ; 8、5、4 ; 7、6、4‎ ‎③分别讨论，看哪组满足题意：此事有两种讨论思路：‎ ‎（1）利用加减数字谜；奥运会×9=梦想成真，‎ ‎∴ 奥 运 会 0‎ ‎ － 奥 运 会 ‎ 梦 想 成 真 ‎∵“奥”≠“梦”，所以， “运”必定比“奥”小，（这样“运”－“奥”时需借位，这样才能保证“奥”≠“梦”）即 奥运会这个三位数的十位比百位小。‎ Ⅰ 若“奥”、“运”、“会”为8、7、2这一组，则 三位数“奥运会”可能为872，827，728 。∵奥运会×9=梦想成真 若： 872×9=7848 “奥”、“真”重复 所以： 不行 ‎ 827×9=7843 “奥”、“想”重复 所以： 不行 ‎ 728×9=6552 “想”、“成”重复 所以： 不行 Ⅱ、Ⅲ一样的思路试 其他三组经试验： 三位数“奥运会”可以为：836，647，638‎ ‎（2）利用乘除数字谜 根据所求，“奥”、“运”、“会”必是下面三组中的一组： ‎ ‎ 8、7、2 8、6、3 8、5、4 7、6、4‎ ‎ 奥 运 会 ‎ ‎ × 9‎ ‎ 梦 想 成 真 ①当“奥”、“运”、“会”为8、7、2一组里的数时，观察尾数，可知会只能为7，‎ 则奥运会可以是287也可以是827，此时梦想成真应从3、4、5、6里选，287×9=2870-287，‎ 千位是2，没有满足这样的数；‎ ‎827×9=8270-827千位是7，也无这样的数；‎ ②当奥”、“运”、“会”为8、3、6一组里的数时，观察尾数，可知会只能为8，也可能为3，‎ 可能为6，分别讨论；‎ 当会为8时，奥运会=638或368，638×9=6380-638=5742，满足；368×9=3680-368=3314不符合；‎ 当会为6时，奥运会=386或836，386×9=3860-386=3474，不符合；836×9=8360-836=7524满足；‎ 当会为3时，奥运会=683或者863，683×9=6830-683，千位为6，不符合；863×9=8630-863=7767不符合；其他同理，发现当奥运会=647也可。所以奥运会有836，647，638共3种取值。‎ ‎【答案】奥运会有836，647，638共3种取值 【例 1】 如下图所示的算式中，除数是( )，商是（　　　）。‎ ‎【考点】除法数字谜 【难度】星 【题型】填空 ‎【关键词】希望杯，5年级，复赛，第12题 【解析】 ‎，突破口为如图中的阶梯型。‎ ‎【答案】除数是，商