数学理卷·2018届黑龙江省哈尔滨师大附中高二4月月考（2017-04）

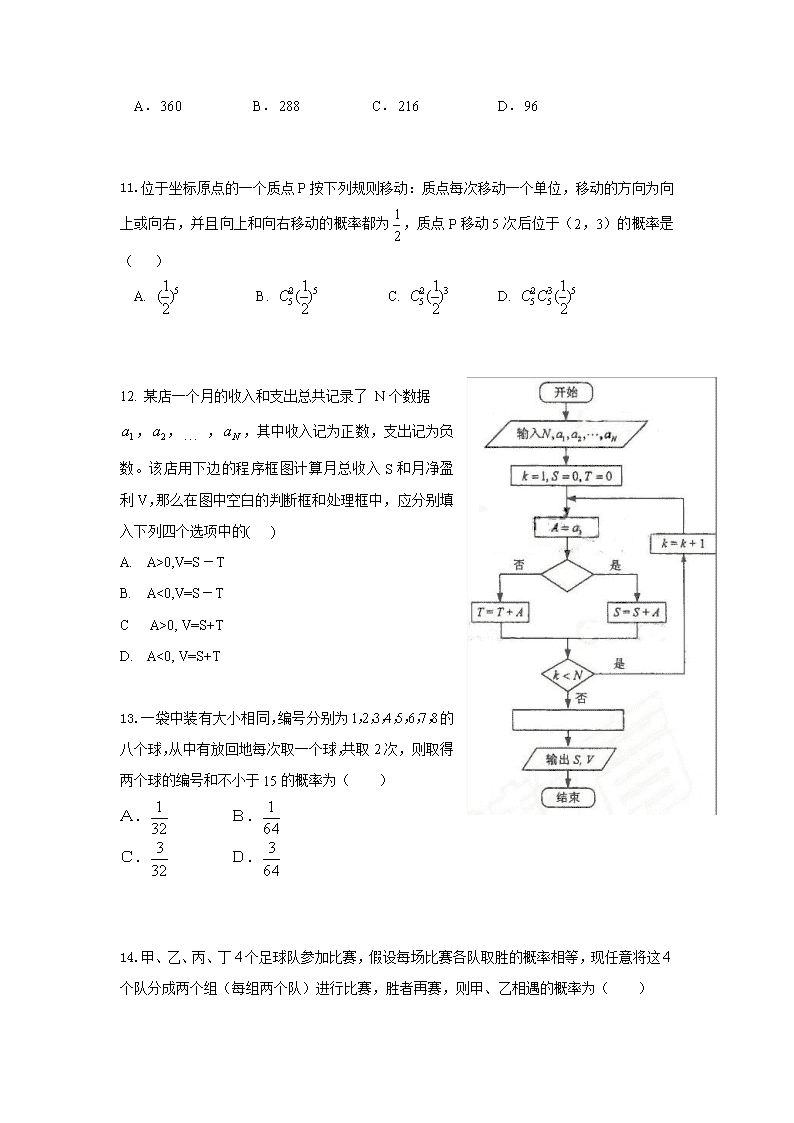
数学理卷·2018届黑龙江省哈尔滨师大附中高二4月月考（2017-04）

哈师大附中2017年高二下学期月考 理科数学试卷 一．选择题（本大题共14小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．若且则的值为( )‎ A. B. C. D.‎ ‎2、某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x（万元）‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y（万元）‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程中的为，据此模型预报广告费用为6万元时销售额 为 （ ）‎ ‎ A．63．6万元 B．65．5万元 C．67．7万元 D．72．0万元 ‎3.已知随机变量服从正态分布N(3,a2),则P(＝( )‎ ‎ A. B. C. D.‎ 4. 某校安排5个班到4个工厂进行社会实践，每个班去一个工厂，每个工厂至少安排一个班，不同的安排方法共有（ ）‎ ‎ A.120种 B.240种 C.264种 D.356种 5. 甲、乙两人进行乒乓球比赛，比赛规则为“3局2胜”，即以先赢2局者为胜．根据经验，每局比赛中甲获胜的概率为0．6，则本次比赛甲获胜的概率是( )‎ ‎ A. 0．216 B. 0．36 C. 0．432 D. 0．648‎ ‎6.在一个口袋中装有5个白球和3个黑球，这些球除颜色外完全相同，从中摸出3个球，至少摸到2个黑球的概率等于（ ）‎ A. B. C. D.‎ ‎7.从甲、乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲、乙两组数据的平均数分别为，，中位数分别为，，则（ ）‎ A. ，‎ B. ，‎ C. ，‎ D. ，‎ ‎8.采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1,2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间的人做问卷，编号落入区间的人做问卷，其余的人做问卷.则抽到的人中，做问卷的人数为( )‎ A.7 B. 9 C. 10 D.15‎ ‎9.某人进行射击训练,每次击中目标的概率为0.7,在10次射击中,未击中目标次数的期望为( )‎ A. 7 B. 3 C. 4 D. 5‎ 10. ‎ 位男生和位女生共位同学站成一排，若男生甲不站两端，位女生中有且只有两位女生相 ‎ ‎ 邻，则不同排法的种数是（ ）‎ A． ‎ B． C． D．‎ ‎11.位于坐标原点的一个质点P按下列规则移动：质点每次移动一个单位，移动的方向为向上或向右，并且向上和向右移动的概率都为，质点P移动5次后位于（2，3）的概率是（ ）‎ A. B. C. D. ‎ 12. ‎ 某店一个月的收入和支出总共记录了 N个数据 ‎，， ，，其中收入记为正数，支出记为负数。该店用下边的程序框图计算月总收入S和月净盈利V，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )‎ A. A>0,V=S－T【来源：全,品…中&高*考+网】‎ B. A<0,V=S－T C A>0, V=S+T【来源：全,品…中&高*考+网】‎ D. A<0, V=S+T ‎13.一袋中装有大小相同，编号分别为的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号和不小于15的概率为（　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎14.甲、乙、丙、丁个足球队参加比赛，假设每场比赛各队取胜的概率相等，现任意将这个队分成两个组（每组两个队）进行比赛，胜者再赛，则甲、乙相遇的概率为（ ）‎ A． B． C． D．‎ ‎ ‎ 开始 S=1,k=1‎ k=k+2‎ s=2s+k k>8?‎ 是 否 输出s 结束 ‎（１5题图）‎ 二．填空题（本大题共6小题，每小题5分）‎ ‎15.某程序框图如图所示，则输出的结果是 ‎16. ‎ ‎17.设一次试验成功的概率为，进行100次独立重复试验，当时，成功次数的标准差最大，其最大值为 18. 从一批含有13只正品,2只次品的产品中,不放回地抽取3次,每次抽一只,设抽取次品数为,则 ‎19.在某项测量中，测量结果服从正态分布．若在内取值的概率为0.4，则在内取值的概率为 ．‎ 20. 甲、乙、丙、丁四位师范生要分到A、B、C三所学校工作，每 ‎ 所学校至少一人，已知甲被分到A校工作，求乙被分到B校工作的概率 ‎ 三．解答题（本大题共3小题，总分50分）‎ ‎21（本小题满分15分）.甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与， ‎ ‎ 且乙投球2次均未命中的概率为．‎ ‎（Ⅰ）求乙投球的命中率；‎ ‎（Ⅱ）求甲投球2次，至少命中1次的概率；‎ ‎（Ⅲ）若甲、乙两人各投球2次，求两人共命中2次的概率．‎ ‎22.（本小题满分15分）要从两名射击运动员中选出一人去参加比赛，现进行选拔赛，每名队员各射击100次，统计结果如下：‎ ‎ ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎2‎ ‎6‎ ‎7‎ ‎60‎ ‎25‎ ‎ 甲队员射击结果：‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎3‎ ‎4‎ ‎13‎ ‎50‎ ‎30‎ ‎ 乙队员射击结果：‎ （1） 如果每次射击成绩为9环或10环记为优秀，分别估计甲乙两名运动员的优秀率。‎ （2） 如果以运动员的平均成绩和发挥稳定性来评价，利用具体的数字特征为依据，分析应选哪位运动员。（可以用上面的频率作为相应的概率来进行计算）‎ ‎ ‎ ‎ 23.（本小题满分20分）微信是现代生活进行信息交流的重要工具，据统计，某公司200名员工中﹪的人使用微信，其中每天使用微信时间在一小时以内的有66人，其余每天使用微信在一小时以上；若将员工年龄分成青年（年龄小于40岁），和中年（年龄不小于40岁）两个阶段，使用微信的人中60﹪是青年人；若规定：每天使用微信时间在一小时以上为经常使用微信，经常使用微信的员工中是青年人.‎ ‎（Ⅰ）若要调查该公司使用微信的员工经常使用微信与年龄的关系，列出列联表；‎ ‎（Ⅱ）由列联表中所得数据，是否有﹪的把握认为经常使用微信与年龄有关？‎ ‎0.05‎ ‎0.01‎ ‎3.841‎ ‎6.635‎ ‎ 高二理科数学月考试题答案2017.4‎ 一． 选择题：CBDBD ABCBB BCDD 二． 填空题：15. 83 16. 17. 18. 3 19. 0.8 20. ‎ ‎21.解：本小题主要考查随机事件、互斥事件、相互独立事件等概率的基础知识，考查运用概率知识解决实际问题的能力．满分12分．‎ ‎（Ⅰ）解法一：设“甲投球一次命中”为事件A，“乙投球一次命中”为事件B．‎ 由题意得 解得或（舍去），所以乙投球的命中率为．‎ 解法二：设设 “甲投球一次命中”为事件A，“乙投球一次命中”为事件B．‎ 由题意得，于是或（舍去），故．‎ 所以乙投球的命中率为．‎ ‎（Ⅱ）解：由题设和（Ⅰ）知．‎ 故甲投球2次至少命中1次的概率为 ‎（Ⅲ）由题设和（Ⅰ）知，‎ 甲、乙两人各投球2次，共命中2次有三种情况：甲、乙两人各中一次；甲中两次，乙两次均不中；甲两次均不中，乙中2次。概率分别为，‎ ‎，‎ 所以甲、乙两人各投两次，共命中2次的概率为．‎ ‎22.（1）估计甲的优秀率为0.85；估计乙的优秀率为0.80‎ ‎（2）.设甲乙两名运动员射击环数分别为和,分布列为:‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎0.02‎ ‎0.06‎ ‎0.07‎ ‎0.6‎ ‎0.25‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎0.03‎ ‎0.04‎ ‎0.13‎ ‎0.5‎ ‎0.3‎ ‎ ‎ 由具体数据可知：甲乙两名运动员平均成绩一样，但甲运动员发挥稳定，所以应选甲运动员参加比赛。‎ ‎23.解:（Ⅰ）由已知可得，该公司员工中使用微信的共：人 ‎ 经常使用微信的有人，其中青年人：人 ‎ 所以可列下面列联表：‎ ‎ ‎ 青年人 中年人 合计 经常使用微信 ‎76‎ ‎38‎ ‎114‎ 不经常使用微信 ‎32‎ ‎34‎ ‎66‎ 合计 ‎108‎ ‎72‎ ‎180‎ ‎ （Ⅱ）将列联表中数据代入公式可得：‎ 所以没有﹪的把握认为经常使用微信与年龄有关.‎