高中数学选修2-3课件3_1 回归分析（ 二）

高中数学选修2-3课件3_1 回归分析（ 二）

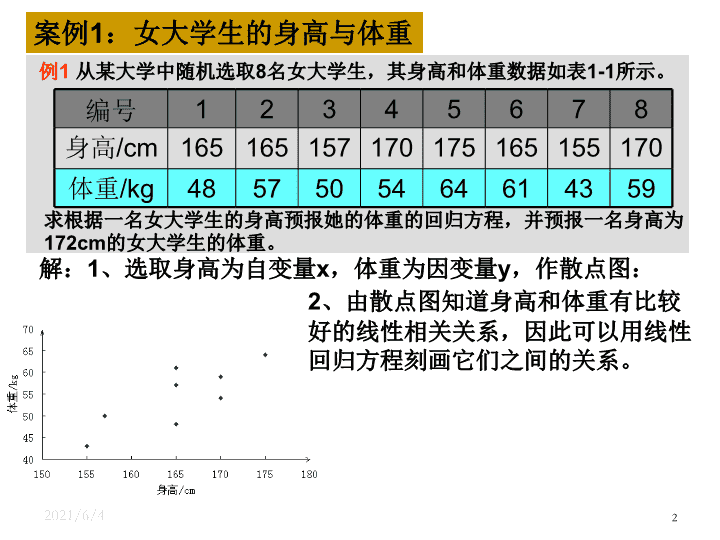
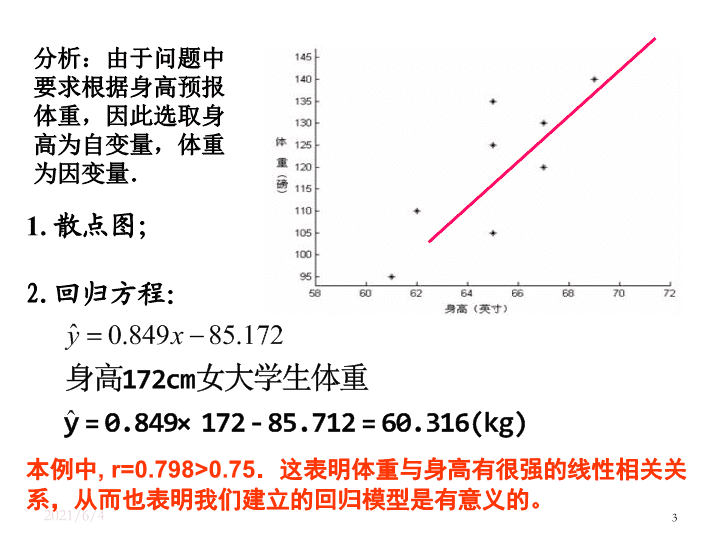
2021/2/13 1 3.1 回归分析的基本思想及其初步应用（二） 高二数学 选修 2-3 2021/2/13 2 例 1 从某大学中随机选取 8 名女大学生，其身高和体重数据如表 1-1 所示。 编号 1 2 3 4 5 6 7 8 身高 /cm 165 165 157 170 175 165 155 170 体重 /kg 48 57 50 54 64 61 43 59 求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172cm 的女大学生的体重。 案例 1 ：女大学生的身高与体重 解： 1 、选取身高为自变量 x ，体重为因变量 y ，作散点图： 2 、由散点图知道身高和体重有比较好的线性相关关系，因此可以用线性回归方程刻画它们之间的关系。 2021/2/13 3 分析：由于问题中要求根据身高预报体重，因此选取身高为自变量，体重为因变量． 2. 回归方程： 1. 散点图； 本例中 , r=0.798>0.75 ．这表明体重与身高有很强的线性相关关系，从而也表明我们建立的回归模型是有意义的。 2021/2/13 4 探究： 身高为 172cm 的女大学生的体重一定是 60.316kg 吗？如果不是，你能解析一下原因吗？ 答：身高为 172cm 的女大学生的体重不一定是 60.316kg ，但一般可以认为她的体重接近于 60.316kg 。 即，用这个回归方程不能给出每个身高为 172cm 的女大学生的体重的预测值，只能给出她们平均体重的值。 2021/2/13 5 例 1 从某大学中随机选取 8 名女大学生，其身高和体重数据如表 1-1 所示。 编号 1 2 3 4 5 6 7 8 身高 /cm 165 165 157 170 175 165 155 170 体重 /kg 48 57 50 54 64 61 43 59 求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172cm 的女大学生的体重。 案例 1 ：女大学生的身高与体重 解： 1 、选取身高为自变量 x ，体重为因变量 y ，作散点图： 2 、由散点图知道身高和体重有比较好的线性相关关系，因此可以用线性回归方程刻画它们之间的关系。 3 、从散点图还看到，样本点散布在某一条直线的附近，而不是在一条直线上，所以 不能用一次函数 y=bx+a 描述它们关系。 2021/2/13 6 我们可以用下面的 线性回归模型 来表示： y=bx+a+e ， (3) 其中 a 和 b 为模型的未知参数， e 称为随机误差 。 y=bx+a+e ， E(e)=0,D(e)= (4) 在线性回归模型 (4) 中，随机误差 e 的 方差 越小 ，通过回归直线 (5) 预报真实值 y 的 精度越高。 随机误差 是引起预报值 与真实值 y 之间的 误差 的原因之一， 其大小取决于随机误差的方差。 另一方面，由于公式 (1) 和 (2) 中 和 为截距和斜率的估计值，它们与真实值 a 和 b 之间也存在误差，这种误差是引起预报值与真实值 y 之间误差的另一个原因。 2021/2/13 7 思考 : 产生随机误差项 e 的原因是什么？ 随机误差 e 的来源 ( 可以推广到一般）： 1 、忽略了其它因素的影响：影响身高 y 的因素不只是体重 x ，可能还包括遗传基因、饮食习惯、生长环境等因素； 2 、用线性回归模型近似真实模型所引起的误差； 3 、身高 y 的观测误差。 以上三项误差越小，说明我们的回归模型的拟合效果越好。 2021/2/13 8 函数模型与回归模型之间的差别 函数模型： 回归模型： 可以提供 选择模型的准则 2021/2/13 9 函数模型与回归模型之间的差别 函数模型： 回归模型： 线性回归模型 y=bx+a+e 增加了随机误差项 e ， 因变量 y 的值由自变量 x 和 随机误差项 e 共同确定 ，即 自变量 x 只能解析部分 y 的变化 。 在统计中，我们也把自变量 x 称为 解析变量 ，因变量 y 称为 预报变量 。 所以，对于身高为 172cm 的女大学生，由回归方程可以预报其体重为 思考： 如何刻画 预报变量（体重）的变化？这个变化在 多大程度 上 与解析变量（身高）有关？在 多大程度 上与随机误差有关？ 假设 身高 和 随机误差 的不同不会对体重产生 任何 影响，那么所有人的体重将相 同。 在体重不受任何变量影响的假设下，设 8 名女大学生的体重都是她们的平均值， 即 8 个人的体重都为 54.5kg 。 54.5 54.5 54.5 54.5 54.5 54.5 54.5 54.5 体重 /kg 170 155 165 175 170 157 165 165 身高 /cm 8 7 6 5 4 3 2 1 编号 54.5kg 在散点图中，所有的点 应该 落在同一条 水平直线上，但是 观测到的数据并非如 此。 这就意味着 预报变量（体重）的值 受解析变量（身高）或随机误差的影响 。 对回归模型进行 统计检验 2021/2/13 11 59 43 61 64 54 50 57 48 体重 /kg 170 155 165 175 170 157 165 165 身高 /cm 8 7 6 5 4 3 2 1 编号 例如，编号为 6 的女大学生的体重并没有落在水平直线上，她的体重为 61kg 。解析 变量（身高）和随机误差共同把这名学生的体重从 54.5kg“ 推”到了 61kg ，相差 6.5kg ， 所以 6.5kg 是 解析变量 和 随机误差 的 组合效应 。 编号为 3 的女大学生的体重并也没有落在水平直线上，她的体重为 50kg 。解析 变量（身高）和随机误差共同把这名学生的体重从 50kg“ 推”到了 54.5kg ，相差 -4.5kg ， 这时 解析变量和随机误差的组合效应为 -4.5kg 。 用这种方法可以对所有预报变量计算组合效应。 数学上，把 每个效应（观测值减去总的平均值）的平方加起来 ，即用 表示 总的效应 ，称为 总偏差平方和 。 在例 1 中，总偏差平方和为 354 。 2021/2/13 12 59 43 61 64 54 50 57 48 体重 /kg 170 155 165 175 170 157 165 165 身高 /cm 8 7 6 5 4 3 2 1 编号 那么，在这个总的效应（总偏差平方和）中，有多少来自于解析变量（身高）？ 有多少来自于随机误差？ 假设随机误差对体重没有影响，也就是说，体重仅受身高的影响，那么散点图 中所有的点将完全落在回归直线上。但是，在图中，数据点并没有完全落在回归 直线上。 这些点散布在回归直线附近，所以一定是随机误差把这些点从回归直线上 “推”开了 。 在例 1 中，残差平方和约为 128.361 。 因此，数据点和它在回归直线上相应位置的差异 是 随机误差的效应 ， 称 为 残差 。 例如，编号为 6 的女大学生，计算随机误差的效应（残差）为： 对每名女大学生计算这个差异，然后分别将所得的值平方后加起来，用数学符号 称为 残差平方和 ， 它代表了 随机误差的效应。 表示为： 即， 类比样本方差估计总体方差的思想，可以用 作为 的估计量 ， 越小，预报精度越高。 2021/2/13 13 由于解析变量和随机误差的总效应（总偏差平方和）为 354 ，而随机误差的效应为 128.361 ，所以 解析变量的效应 为 解析变量和随机误差的总效应（总偏差平方和） = 解析变量的效应（回归平方和） + 随机误差的效应（残差平方和） 354-128.361=225.639 这个值称为 回归平方和。 我们可以用 相关指数 R 2 来刻画回归的效果，其计算公式是 2021/2/13 14 离差平方和的分解 （三个平方和的意义） 总偏差平方和 ( SST ) 反映因变量的 n 个观察值与其均值的总离差 回归平方和 ( SSR ) 反映自变量 x 的变化对因变量 y 取值变化的影响，或者说，是由于 x 与 y 之间的线性关系引起的 y 的取值变化，也称为可解释的平方和 残差平方和 ( SSE ) 反映除 x 以外的其他因素对 y 取值的影响，也称为不可解释的平方和或剩余平方和 2021/2/13 15 样本决定系数 （判定系数 R 2 ） 1. 回归平方和占总离差平方和的比例 反映回归直线的拟合程度 取值范围在 [ 0 , 1 ] 之间 R 2 1 ，说明回归方程拟合的越好； R 2 0 ，说明回归方程拟合的越差 判定系数等于相关系数的平方，即 R 2 ＝ ( r ) 2 2021/2/13 16 显然， R 2 的值越大，说明残差平方和越小，也就是说模型拟合效果越好。 在线性回归模型中， R 2 表示解析变量对预报变量变化的贡献率。 R 2 越接近 1 ，表示回归的效果越好（因为 R 2 越接近 1 ，表示解析变量和预报变量的 线性相关性越强） 。 如果某组数据可能采取几种不同回归方程进行回归分析，则可以通过比较 R 2 的值 来做出选择，即选取 R 2 较大的模型作为这组数据的模型。 总的来说： 相关指数 R 2 是度量模型拟合效果的一种指标。 在线性模型中，它 代表自变量刻画预报变量的能力 。 我们可以用 相关指数 R 2 来刻画回归的效果，其计算公式是 2021/2/13 17 1 354 总计 0.36 128.361 残差变量 0.64 225.639 随机误差 比例 平方和 来源 表 1-3 从表 3-1 中可以看出，解析变量对总效应约贡献了 64% ，即 R 2 0.64 ，可以叙述为 “身高解析了 64% 的体重变化”，而随机误差贡献了剩余的 36% 。 所以，身高对体重的效应比随机误差的效应大得多。 我们可以用 相关指数 R 2 来刻画回归的效果，其计算公式是 2021/2/13 18 表 3-2 列出了女大学生身高和体重的原始数据以及相应的残差数据。 在研究两个变量间的关系时，首先要根据散点图来粗略判断它们是否线性相关， 是否可以用回归模型来拟合数据。 残差分析与残差图的定义： 然后，我们可以通过残差 来判断模型拟合的效果，判断原始 数据中是否存在可疑数据， 这方面的分析工作称为残差分析 。 编号 1 2 3 4 5 6 7 8 身高 /cm 165 165 157 170 175 165 155 170 体重 /kg 48 57 50 54 64 61 43 59 残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382 我们可以利用图形来分析残差特性，作图时纵坐标为残差，横坐标可以选为样本 编号，或身高数据，或体重估计值等，这样作出的图形称为 残差图 。 2021/2/13 19 残差图的制作及作用。 坐标纵轴为残差变量，横轴可以有不同的选择； 若模型选择的正确，残差图中的点应该分布在以横轴为心的带形区域 ； 对于远离横轴的点，要特别注意 。 身高与体重残差图 异常点 错误数据 模型问题 几点说明： 第一个样本点和第 6 个样本点的残差比较大，需要确认在采集过程中是否有人为的错误。如果数据采集有错误，就予以纠正，然后再重新利用线性回归模型拟合数据；如果数据采集没有错误，则需要寻找其他的原因。 另外，残差点比较均匀地落在水平的带状区域中，说明选用的模型计较合适，这样的带状区域的宽度越窄，说明模型拟合精度越高，回归方程的预报精度越高。 2021/2/13 20 例 2 、在一段时间内，某中商品的价格 x 元和需求量 Y 件之间的一组数据为： 求出 Y 对的回归直线方程，并说明拟合效果的好坏。 价格 x 14 16 18 20 22 需求量 Y 12 10 7 5 3 解： 2021/2/13 21 例 2 、在一段时间内，某中商品的价格 x 元和需求量 Y 件之间的一组数据为： 求出 Y 对的回归直线方程，并说明拟合效果的好坏。 价格 x 14 16 18 20 22 需求量 Y 12 10 7 5 3 列出残差表为 0.994 因而，拟合效果较好。 0 0.3 -0.4 -0.1 0.2 4.6 2.6 -0.4 -2.4 -4.4 2021/2/13 22 用身高预报体重时，需要注意下列问题： 1 、回归方程只适用于我们所研究的样本的总体； 2 、我们所建立的回归方程一般都有时间性； 3 、样本采集的范围会影响回归方程的适用范围； 4 、不能期望回归方程得到的预报值就是预报变量的精确值。 事实上，它是预报变量的可能取值的平均值。 —— 这些问题也使用于其他问题。 涉及到统计的一些思想： 模型适用的总体； 模型的时间性； 样本的取值范围对模型的影响； 模型预报结果的正确理解。 小结 2021/2/13 23 一般地，建立回归模型的基本步骤为： （ 1 ）确定研究对象，明确哪个变量是解析变量，哪个变量是预报变量。 （ 2 ）画出确定好的解析变量和预报变量的散点图，观察它们之间的关系 （如是否存在线性关系等）。 （ 3 ）由经验确定回归方程的类型（如我们观察到数据呈线性关系，则选用线性回归方程 y=bx+a ） . （ 4 ）按一定规则估计回归方程中的参数（如最小二乘法）。 （ 5 ）得出结果后分析残差图是否有异常（个别数据对应残差过大，或残差呈现不随机的规律性，等等），过存在异常，则检查数据是否有误，或模型是否合适等。 2021/2/13 24 什么是回归分析？ （内容） 从一组样本数据出发，确定变量之间的数学关系式 对这些关系式的可信程度进行各种统计检验， 并从影响某一特定变量的诸多变量中找出哪些变量的影响显著，哪些不显著 利用所求的关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精确程度 2021/2/13 25 回归分析与相关分析的区别 相关分析中，变量 x 变量 y 处于平等的地位；回归分析中，变量 y 称为因变量，处在被解释的地位， x 称为自变量，用于预测因变量的变化 相关分析中所涉及的变量 x 和 y 都是随机变量；回归分析中，因变量 y 是随机变量，自变量 x 可以是随机变量，也可以是非随机的确定变量 相关分析主要是描述两个变量之间线性关系的密切程度；回归分析不仅可以揭示变量 x 对变量 y 的影响大小，还可以由回归方程进行预测和控制