- 2021-06-18 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
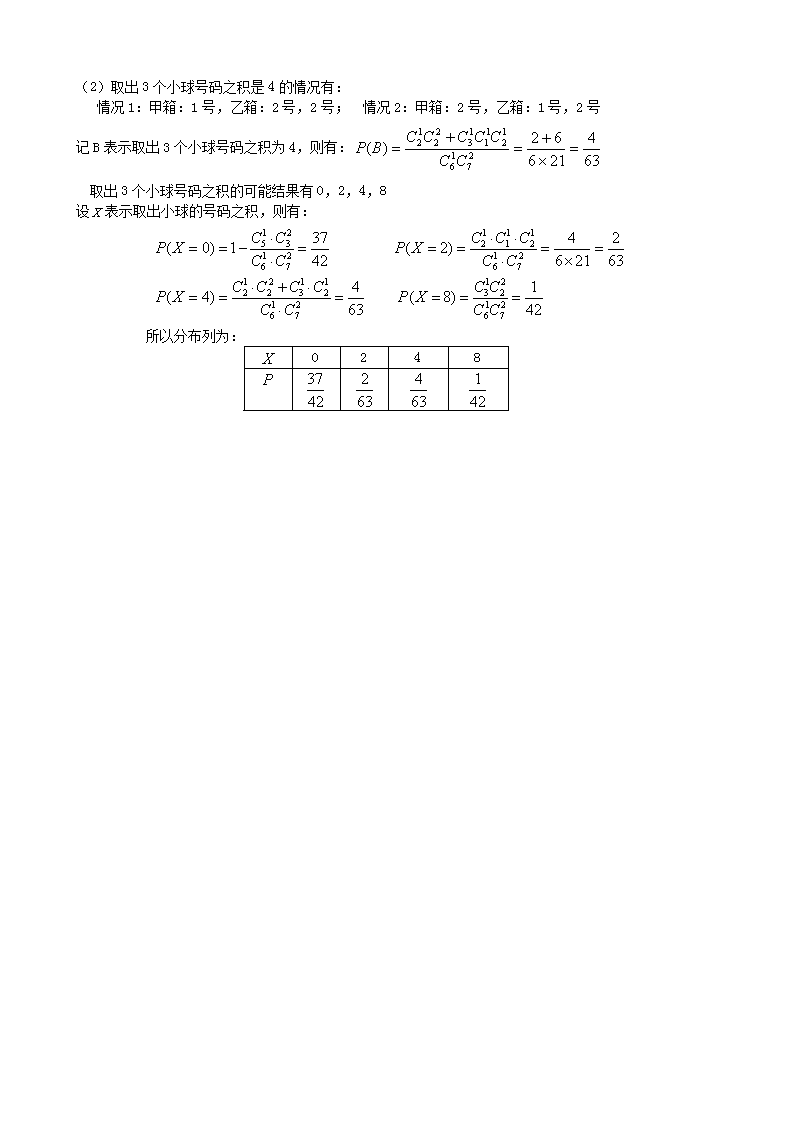
高中数学:新人教A版选修2-3 2_2二项分布及其应用(同步练习)
高中数学系列2—3单元测试题(2.2) 一、选择题: 1、已知随机变量服从二项分布,,则(等于( ) A. B. C. D. 2设某批电子手表正品率为,次品率为,现对该批电子手表进行测试,设第次首次测到正品,则等于( ) A. B. C. D. 3、设随机变量的概率分布列为,则的值为( ) A B C D 4、10个球中有一个红球,有放回的抽取,每次取出一球,直到第次才取得次红球的概率为( ) A. B. C. D. 5、甲、乙两名篮球队员轮流投篮直至某人投中为止,设甲每次投篮命中的概率为,乙投中的概率为,而且不受其他次投篮结果的影响,设投篮的轮数为,若甲先投,则等于( ) A. B. C. D. 6、某学生解选择题出错的概率为,该生解三道选择题至少有一道出错的概率是( ) A. B. C. D. 7、一个口袋内有带标号的7个白球,3个黑球,作有放回抽样,连摸2次,每次任意摸出1球,则2次摸出的球为一白一黑的概率是( ) A. B. C. D. 8、用个均匀材料做成的各面上分别标有数字的正方体玩具,每次同时抛出,共抛次,则至少有一次全部都是同一数字的概率是( ) A. B. C. D. 二、填空题: 9、某人射击1次,击中目标的概率是0.8,他射击4次,至少击中3次的概率是 . 10、三人独立地破译一个密码,它们能译出的概率分别为、、,则能够将此密码译出的概率为 . 11、设随机变量~B(2, ),随机变量~B(3, ),若,则 . 三、解答题: 12、某一射手射击所得环数分布列为 4 5 6 7 8 9 10 0.02 0.04 0.06 0.09 0.28 0.29 0.22 求此射手“射击一次命中环数≥7”的概率 13、某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数的概率分布 14、有甲乙两个箱子,甲箱中有6个小球,其中1个标记0号,2个小球标记1号,3个小球标记2号;乙箱装有7个小球,其中4个小球标记0号,一个标记1号,2个标记2号。从甲箱中取一个小球,从乙箱中取2个小球,一共取出3个小球。求: (1)取出的3个小球都是0号的概率; (2)取出的3个小球号码之积是4的概率; 高中数学系列2—3单元测试题(2.2)参考答案 一、选择题: 1、D 2、C 3、D 4、C 5、B 6、D 7、D 8、D 二、填空题: 9、 1.4336 10、 11、 三、解答题: 12、解:“射击一次命中环数≥7”是指互斥事件“=7”,“=8”,“=9”,“=10”的和,根据互斥事件的概率加法公式,有: P(≥7)=P(=7)+P(=8)+P(=9)+P(=10)=0.88 13、解:的取值分别为0、1、2 表示抽取两件均为正品 ∴ 表示抽取一件正品一件次品 表示抽取两件均为次品 ∴的概率分布为: 0 1 2 0.9025 0.095 0.0025 14、解:(1)欲使取出3个小球都为0号,则必是在甲箱中取出0号球并且在乙箱中从4个0号球中取出另外2个0号小球 记A表示取出3个0号球则有: (2)取出3个小球号码之积是4的情况有: 情况1:甲箱:1号,乙箱:2号,2号; 情况2:甲箱:2号,乙箱:1号,2号 记B表示取出3个小球号码之积为4,则有: 取出3个小球号码之积的可能结果有0,2,4,8 设表示取出小球的号码之积,则有: 所以分布列为: 0 2 4 8查看更多