- 2021-06-17 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
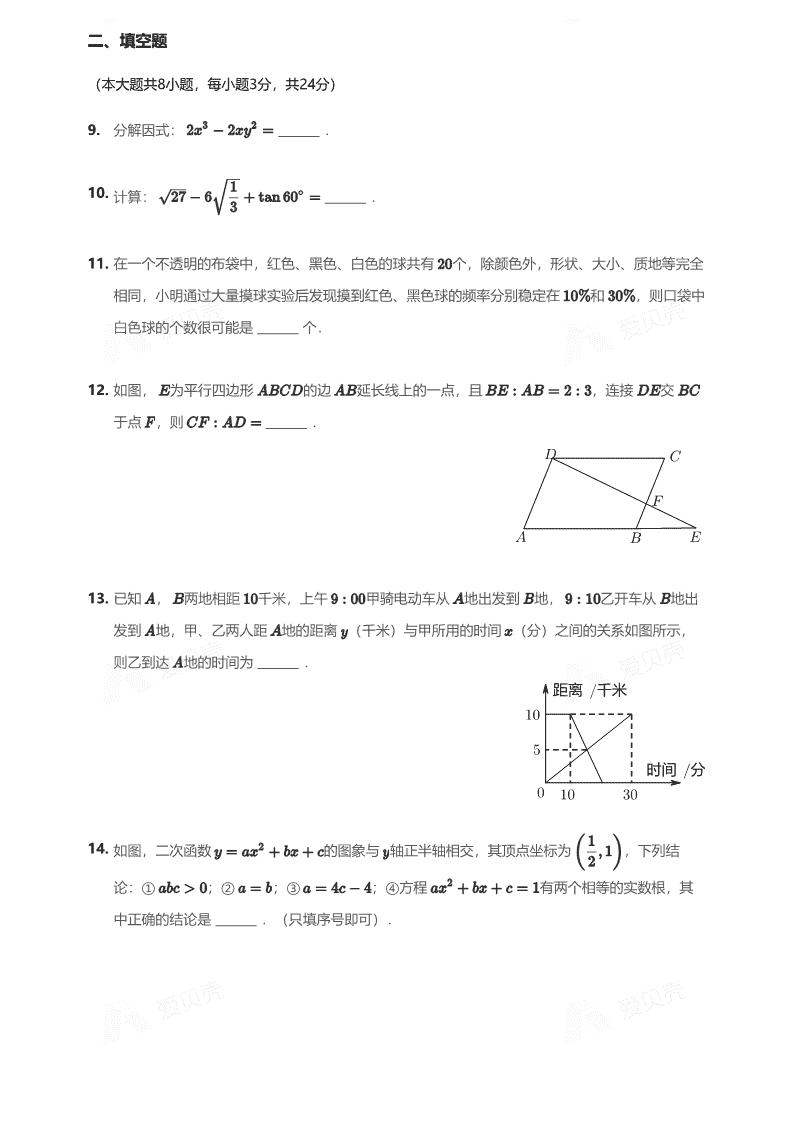
2017年辽宁锦州中考真题数学试卷
/ 2017年辽宁锦州中考真题数学试卷 一、选择题 (本大题共8小题,每小题2分,共16分) 1. A. B. C. D. 的绝对值是( ). 2. A. B. C. D. 联合国宽带委员会 年 月 日发布了《 年宽带状况》报告,报告显示,中国以 亿 网民人数成为全球第一大互联网市场, 亿用科学记数法表示为( ). 3. A. B. C. D. 如图,一个由相同小正方体堆积而成的几何体,该几何体的主视图是( ). 4. A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 没有实数根 D. 无法判断 关于 的一元二次方程 根的情况是( ). 5. / A. B. C. D. 一小区大门的栏杆如图所示,当栏杆抬起时, 垂直于地面 , 平行于地面 ,则 的度数为( ). 6. A. , B. , C. , D. , 在某校开展的“书香校园”读书活动中,学校为了解八年级学生的读书情况,随机调查了八年级 名学生每学期每人读书的册数,绘制统计表如下: 册数 人数 则这 个样本数据的众数和中位数分别是( ). 7. A. B. C. D. 如图,四边形 是⊙ 的内接四边形, 与 的延长线交于点 , 与 的延长线 交于点 , , ,则 的度数为( ). 8. A. B. C. D. 如图,矩形 中, , ,双曲线 的图象分别交 , 于点 , ,连接 , , , ,则 值为( ). / 二、填空题 (本大题共8小题,每小题3分,共24分) 9. 分解因式: . 10. 计算: . 11. 在一个不透明的布袋中,红色、黑色、白色的球共有 个,除颜色外,形状、大小、质地等完全 相同,小明通过大量摸球实验后发现摸到红色、黑色球的频率分别稳定在 和 ,则口袋中 白色球的个数很可能是 个. 12. 如图, 为平行四边形 的边 延长线上的一点,且 ,连接 交 于点 ,则 . 13. 已知 , 两地相距 千米,上午 甲骑电动车从 地出发到 地, 乙开车从 地出 发到 地,甲、乙两人距 地的距离 (千米)与甲所用的时间 (分)之间的关系如图所示, 则乙到达 地的时间为 . 距离 千米 时间 分 14. 如图,二次函数 的图象与 轴正半轴相交,其顶点坐标为 ,下列结 论:① ;② ;③ ;④方程 有两个相等的实数根,其 中正确的结论是 .(只填序号即可). / 15. 如图,正方形 中, , 是 中点,将正方形 沿 折叠,使点 的对 应点 落在 上,延长 交 于点 ,则 的长为 . 16. 如图, 在平面直角坐标系内, , ,以 为直角 边向外作 ,使 , ,以 为直角边向外作 ,使 , ,按此方法进行下去,得到 , , , ,若点 ,则点 的横坐标为 . 三、解答题 (本大题共2小题,共14分) 17. 先化简,再求值: ,其中 . 18. 今年市委市政府积极推进创建“全国文明城市”工作,市创城办公室为了调查初中学生对“社会 主义核心价值观”内容的了解程度(程度分为:“ ﹣十分熟悉”,“ ﹣了解较多”,“ ﹣ 了解较少”,“ ﹣不知道”),对我市一所中学的学生进行了随机抽样调查,根据调查结果绘 制了两幅不完整的统计图如图,根据信息解答下列问题: / ( 1 ) ( 2 ) ( 3 ) ( 4 ) 本次抽样调查了多少名学生. 补全条形统计图和扇形统计图. 求扇形统计图中“ ﹣不知道”所在的扇形圆心角的度数. 若该中学共有 名学生,请你估计这所中学的所有学生中,对“社会主义核心价值观” 内容的了解程度为“十分熟悉”和“了解较多”的学生共有多少名. 四、解答题 (本大题共2小题,每小题8分,共16分) 19. ( 1 ) ( 2 ) 传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅 粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同. 小文吃前两个粽子刚好都是花生馅粽的概率为 . 若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可 能性是否会增大.请说明理由. 20. ( 1 ) ( 2 ) 某电子超市销售甲、乙两种型号的蓝牙音箱,每台进价分别为 元, 元,下表是近两周的 销售情况: 销售时段 销售数量 销售收入 甲种型号 乙种型号 第一周 台 台 元 第二周 台 台 元 求甲、乙两种型号蓝牙音箱的销售单价. 若超市准备用不多于 元的资金再采购这两种型号的蓝牙音箱共 台,求甲种型号的 蓝牙音箱最多能采购多少台. 五、解答题 (本大题共2小题,每小题8分,共16分) / 21. 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路 上,小型车限速为每小时 千米,设置在公路旁的超速监测点 ,现测得一辆小型车在监测点 的南偏西 方向的 处, 秒后,测得其在监测点 的南偏东 方向的 处,已知 米, 在 的北偏东 方向,请问:这辆车超速了吗.通过计算说明理由.(参考数据: , ) 22. ( 1 ) ( 2 ) 已知:四边形是菱形,以为圆心作⊙,与相切于点,交于,交于,连接,. 求证:是⊙的切线; 连接交于点,若,求证:. 六、解答题 (本大题共1小题,共10分) 23. 1 2 ( 1 ) ( 2 ) 为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出 的费用(包括设施维修费、管理人员工资等)为元,为制定合理的收费标准,该商场对每天轿车 停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次 轿车的停车费定价不超过元时,每天来此停放的轿车都为辆次;若每辆次轿车的停车费定价超 过元,则每超过元,每天来此停放的轿车就减少辆次,设每辆次轿车的停车费元(为便于结算, 停车费只取整数),此停车场的日净收入为元(日净收入每天共收停车费每天固定的支出)回答 下列问题: 回答下列问题: 当时,与的关系式为: . 当时,与的关系式为: . 停车场能否实现元的日净收入.如能实现,求出每辆次轿车的停车费定价,如不能实现, 请说明理由. / ( 3 )该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收 入,按此要求,每辆次轿车的停车费定价应定为多少元.此时最大日净收入是多少元. 七、解答题 24. ( 1 ) ( 2 ) ( 3 ) 已知:和均为等边三角形,连接,,点,,分别为,,中点. 当绕点旋转时,如图,则的形状为 ,说明理由. 图 在旋转的过程中,当,,三点共线时,如图,若,,求线段的长. 图 在旋转的过程中,若,,则的周长是否存在最大值和最小值,若存在,直接写出最大值和 最小值.若不存在,说明理由. 备用图 25. 如图,抛物线经过,两点,与轴另一交点为,点是线段上一动点,过点的直线轴,分别交直线、 抛物线于点,. / ( 1 ) ( 2 ) ( 3 ) x y O x y O 备用图 求抛物线的解析式. 是否存在点,使,若存在,求出点的横坐标,若不存在,说明理由. 连接,一动点从点出发,沿线段以每秒个单位的速度运动到,再沿线段以每秒个单位的速 度运动到后停止,当点的坐标是多少时,点在整个运动过程中用时最少.查看更多