四川省德阳市2020届高三（高中2017级）“二诊”考试 数学（文）试题（PDF版）

四川省德阳市2020届高三（高中2017级）“二诊”考试 数学（文）试题（PDF版）

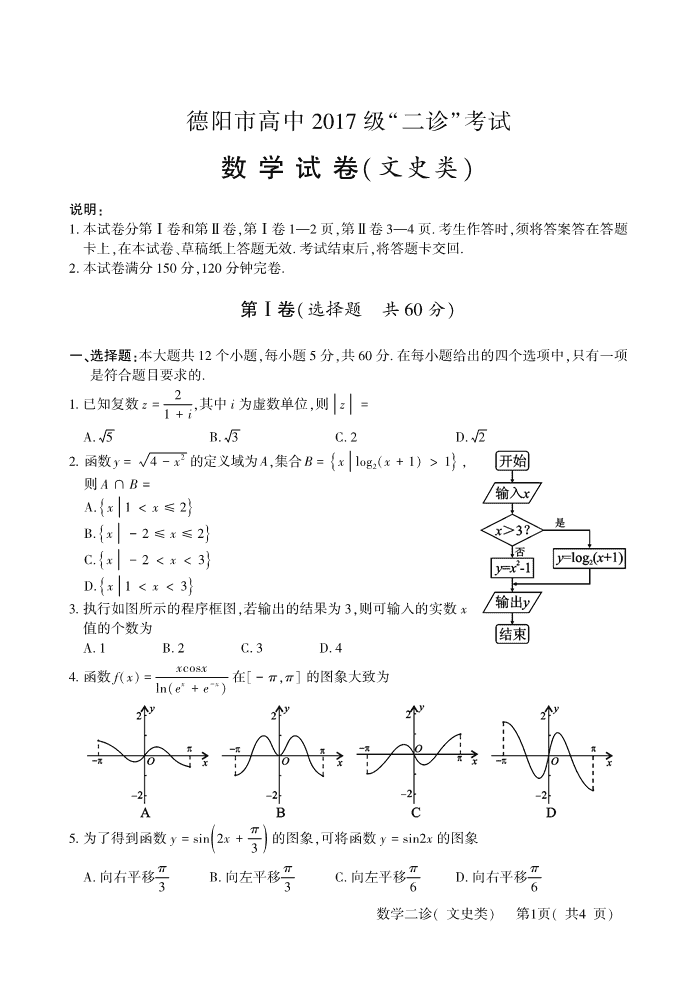
德阳市高中 2017 级“二诊”考试 数 学 试 卷(文史类) 说明: 1. 本试卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷 1—2 页,第Ⅱ卷 3—4 页. 考生作答时,须将答案答在答题 卡上,在本试卷、草稿纸上答题无效. 考试结束后,将答题卡交回. 2. 本试卷满分 150 分,120 分钟完卷. 第 Ⅰ 卷(选择题 　 共 60 分) 一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分. 在每小题给出的四个选项中,只有一项 是符合题目要求的. 1. 已知复数 z = 2 1 + i,其中 i 为虚数单位,则 z = A. 5 B. 3 C. 2 D. 2 2. 函数 y = 4 - x2 的定义域为 A,集合 B = x log2(x + 1) > 1{ } , 则 A ∩ B = A. x 1 < x ≤ 2{ } B. x - 2 ≤ x ≤ 2{ } C. x - 2 < x < 3{ } D. x 1 < x < 3{ } 3. 执行如图所示的程序框图,若输出的结果为 3,则可输入的实数 x 值的个数为 A. 1 B. 2 C. 3 D. 4 4. 函数 f(x) = xcosx ln(ex + e -x ) 在[ - π,π] 的图象大致为 5. 为了得到函数 y = sin 2x + π 3 ( ) 的图象,可将函数 y = sin2x 的图象 A. 向右平移 π 3 B. 向左平移 π 3 C. 向左平移 π 6 D. 向右平移 π 6 )页4共(页1第　)类史文(诊二学数 6. 已知 a = 2 - 1 2 ,b = 1 3 ( ) 1 3 ,c = log 1 2 1 5 ,则 A. b < a < c B. a < b < c C. c < b < a D. b < c < a 7. 已知 l 为抛物线 x2 = 4y 的准线,抛物线上的点 M 到 l 的距离为 d,点 P 的坐标为(4,1), 则 MP + d 的最小值是 A. 17 B. 4 C. 2 D. 1 + 17 8. 不等式组 2x - y ≥ 0 y ≥ 1 2 x x + y - 3 ≤ 0 ì î í ï ï ïï 表示的平面区域为 Ω,则 A. ∀(x,y) ∈ Ω,x + 2y > 3 B. ∃(x,y) ∈ Ω,x + 2y > 5 C. ∀(x,y) ∈ Ω, y + 2x - 1 > 3 D. ∃(x,y) ∈ Ω, y + 2x - 1 > 5 9. 平行四边形 ABCD 中,已知 AB = 4,AD = 3,点 E、F 分别满足AE→ = 2ED→,DF→ =FC→,且 AF→·BE→ = - 6,则向量AD→ 在AB→ 上的投影为 A. 2 B. - 2 C. 3 2 D. - 3 2 10. 已知 △ABC 的内角 A、B、C 的对边分别为 a、b、c,且 A = 60°,b = 3,AD 为 BC 边上的中线,若 AD = 7 2 ,则 △ABC 的面积为 A. 25 3 4 B. 15 3 4 C. 15 4 D. 35 3 4 11. 已知实数 a > 0,a ≠ 1,函数 f(x) = ax ,x < 1 x2 + 4x + alnx,x ≥ 1 { 在 R 上单调递增,则实数 a 的取 值范围是 A. 1 < a ≤ 2 B. a < 5 C. 3 < a < 5 D. 2 ≤ a ≤ 5 12. △ABC 是边长为 2 3 的等边三角形,E、F 分别在线段 AB、AC 上滑动,EF ∥ BC,沿 EF 把 △AEF 折起,使点 A 翻折到点 P 的位置,连接 PB、PC,则四棱锥 P - BCFE 的体积的最大值 为 A. 2 2 B. 3 C. 3 D. 2 第 Ⅱ 卷(非选择题 　 共 90 分) 本卷包括必考题和选考题两部分,第 13 ~ 21 题为必考题,每个试题考生都必须作答,第 22、23 题为选考题,考生根据要求作答. 二、填空题:共 4 小题,每小题 5 分,共 20 分. 将答案填在答题卡上. 13. 已知函数 f(x) = x2 + ax 的图象在点 A(1,f(1)) 处的切线与直线 l:x - 3y + 2 = 0 垂直, )页4共(页2第　)类史文(诊二学数 则实数 a 的值为 　 　 　 　 　 　 . 14. 在一个袋子中装有分别标注 1、2、3、4、5 的 5 个小球,这些小球除标注的数字外完全相 同,现从中随机取出 2 个小球, 则取出的小球标注的数字之差的绝对值为 2 或 4 的概率是 　 　 　 　 　 　 . 15. 已知 a、b 为正实数,直线 x + y + 1 = 0 截圆(x - a) 2 + (y - b) 2 = 4 所得的弦长为 2 2 ,则 ab 的最大值为 　 　 　 　 　 　 . 16. 在 △ABC 中,B、C 的坐标分别为( - 2 2 ,0),(2 2 ,0),且满足 sinB - sinC = 2 2 sinA,O 为坐标原点,若点 P 的坐标为(4,0),则AO→·AP→ 的取值范围为 　 　 　 　 　 　 . 三、解答题:解答应写出文字说明、证明过程或演算步骤. 17. (本题满分 12 分) 已知数列{an } 满足:2 1 ·a 1 + 2 2 ·a 2 + 2 3 ·a 3 + … + 2 n ·an = (n - 1)·2 n+1 + 2 对一切 n ∈ N∗ 成立. (1) 求数列{an } 的通项公式; (2) 求数列 1an ·an+2 { } 的前 n 项和 Sn . 18. (本题满分 12 分) 如图,四棱锥 P - ABCD 的底面 ABCD 中,△ABD 为等边三 角形,△BCD 是等腰三角形,且顶角 ∠BCD = 120°,PC ⊥ BD, 平面 PBD ⊥ 平面 ABCD,M 为 PA 中点. (1) 求证:DM ∥ 平面 PBC; (2) 若 AB = 2 3 ,PD ⊥ PB,求三棱锥 P - BDM 的体积. 19. (本题满分 12 分) 贫困人口全面脱贫是全面建成小康社会的标志性指 标. 党的十九届四中全会提出“坚决打赢脱贫攻坚战,建 立解决相对贫困的长效机制” 对当前和下一个阶段的扶 贫工作进行了前瞻性的部署,即 2020 年要通过精准扶贫 全面消除绝对贫困,实现全面建成小康社会的奋斗目标. 为了响应党的号召,某市对口某贫困乡镇开展扶贫工作. 对某种农产品加工生产销售进行指导,经调查知,在一个 销售季度内,每售出一吨该产品获利 5 万元,未售出的商品,每吨亏损 2 万元. 根据往年的销售 经验,得到一个销售季度内市场需求量的频率分布直方图如图所示. 设该厂在下个销售周期内 生产 210 吨该产品,以 x(单位:吨,180 ≤ x ≤ 230) 表示下一个销售周期市场的需求量,Y(单 位:万元) 表示下一个销售周期市场的销售总利润,视 x 分布在各区间内的频率为相应的概率. )页4共(页3第　)类史文(诊二学数 (1) 求实数 a 的值; (2) 将 Y 表示成 x 的函数,并求出解析式; (3) 估计销售利润不少于 910 万元的概率. 20. (本题满分 12 分) 已知椭圆 C: x2 a2 + y2 b2 = 1(a > b > 0) 的离心率为 5 5 ,右焦点为抛物线 y2 = 4x 的焦点 F. (1) 求椭圆 C 的标准方程; (2)O 为坐标原点,过 O 作两条射线,分别交椭圆于 M、N 两点,若 OM、ON 斜率之积为 - 4 5 , 求证:△MON 的面积为定值. 21. (本题满分 12 分) 已知函数 f(x) = eax - x(a ∈ R,e 为自然对数的底数). (1) 若 f(x) 有两个零点,求实数 a 的取值范围; (2) 若 f(x) 有两个零点 x 1 、x 2 ,且 x 1 < x 2 ,求证:x 1 ·x 2 > e2 . 请考生在 22、23 二题中任选一题作答. 注意:只能做所选定的题目. 如果多做,则按所做第 一个题目计分,做答时,请用 2B 铅笔在答题卡上将所选题号后的方框涂黑. 22. [选修 4 - 4:坐标系与参数方程](本题满分 10 分) 已知点 A 为圆 C:(x - 1) 2 + y2 = 1 上的动点,O 为坐标原点,过 P(0,4) 作直线 OA 的垂线 (当 A、O 重合时,直线 OA 约定为 y 轴),垂足为 M,以 O 为极点,x 轴的正半轴为极轴建立极坐 标系. (1) 求点 M 的轨迹的极坐标方程; (2) 直线 l 的极坐标方程为 ρsin θ + π 3 ( ) = 4,连接 OA 并延长交 l 于 B,求 OA OB 的最大值. 23. [选修 4 - 5:不等式选讲](本题满分 10 分) 已知函数 f(x) = x + 1 . (1) 求不等式 f(x) ≤ 4 - 2x - 3 的解集; (2) 若正数 m、n 满足 m + 2n = mn,求证:f(m) + f( - 2n) ≥ 8. )页4共(页4第　)类史文(诊二学数 德阳市高中 2017 级“二诊”试题 数学参考答案与评分标准 (文史类) 一、选择题 (每小题 5 分,共 60 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A C A C A B D C B D D 二、填空题 (每小题 5 分,共 20 分) 13. - 5　 　 14. 2 5 　 　 15. 1 4 　 　 16. (12, + ∞ ). 三、解答题 17. 解:(1) ∵ 2 1 ·a 1 + 2 2 ·a 2 + 2 3 ·a 3 + … + 2 n ·an = (n - 1)·2 n+1 + 2　 　 ① ∴ 当 n = 1 时,2 1 ·a 1 = 2 ∴ a 1 = 1 2 分…………………………………………………………………… 当 n ≥ 2 时,2 1 ·a 1 + 2 2 ·a 2 + 2 3 ·a 3 + … + 2 n-1 ·an-1 = (n - 2)·2 n + 2　 　 ② ① - ② 得:2 n ·an = n·2 n ∴ an = n 适合 a 1 = 1,故 an = n. 6 分……………………………………………………… (2) 1an ·an+2 = 1n(n + 2) = 1 2 1n - 1n + 2 ( ) 8 分…………………………………… ∴ Sn = 1 2 1 1 - 1 3 ( ) + 1 2 - 1 4 ( ) + 1 3 - 1 5 ( ) + … + 1n - 1n + 2 ( )é ë êê ù û úú = 1 2 1 + 1 2 - 1n + 1 - 1n + 2 ( ) = n(3n + 5) 4(n + 1)(n + 2) . 12 分……………… 18. (1) 证明:设 AB 中点为 N,连接 MN、DN ∵ △ABD 为等边三角形 ∴ DN ⊥ AB ∵ DC = CB,∠DCB = 120° )页7共(　　页1第案答)类史文(学数级7102高 ∴ ∠CBD = 30° ∴ ∠ABC = 60° + 30° = 90° 即 CB ⊥ AB ∵ DN ⊥ AB　 　 ∴ DN ∥ BC ∵ BC ⊂ 平面 PBC,DN ⊄ 平面 PBC ∴ DN ∥ 平面 PBC 2 分……………………………………………………… ∵ MN 为 △PAB 的中位线 ∴ MN ∥ PB ∵ PB ⊂ 平面 PBC,MN ⊄ 平面 PBC ∴ MN ∥ 平面 PBC 4 分……………………………………………………… ∵ MN、DN 为平面 DMN 内二相交直线 ∴ 平面 DMN ∥ 平面 PBC ∵ DM ⊂ 平面 DMN ∴ DM ∥ 平面 PBC. 6 分……………………………………………………… (2) 解:设 BD 中点为 O,连接 AO、CO ∵ △ABD 为等边三角形,△BCD 是等腰三角形,且顶角 ∠BCD = 120° ∴ AO ⊥ BD,CO ⊥ BD　 　 ∴ A、C、O 共线 ∵ PC ⊥ BD,BD ⊥ CO,PC ∩ CO = C,PC,CO ⊂ 平面 PCO ∴ BD ⊥ 平面 PCO. 7 分………………………………………………………… ∵ PO ⊂ 平面 PCO　 　 ∴ BD ⊥ PO ∵ 平面 PBD ⊥ 平面 ABCD,交线为 BD,PO ⊂ 平面 PBD ∴ PO ⊥ 平面 ABCD. 8 分……………………………………………………… ∵ AB = 2 3 　 　 ∴ AO = 3 ∵ PD ⊥ PB,O 为 BD 中点 ∴ PO = 1 2 BD = 3 10 分……………………………………………………… ∴ VP-BDM = 1 2 VP-ABD = 1 2 · 1 3 ·S △ABD ·PO = 1 6 × 1 2 × AO × BD × PO = 3 2 . 12 分………………………………………………………………………… 19. 解:(1) 由(0. 01 + 0. 015 + a + 0. 03 + 0. 01) × 10 = 1 得: a = 0. 035. 4 分…………………………………………………………………… (2) 当 x ≥ 210 时,Y = 210 × 5 = 1050 5 分……………………………………… )页7共(　　页2第案答)类史文(学数级7102高 当 x < 210 时,Y = 5x - (210 - x) × 2 = 7x - 420 7 分……………………… ∴ Y = 7x - 420　 180 ≤ x < 210 1050　 　 　 210 ≤ x ≤ 230 { 8 分………………………………………… (3) 当 210 ≤ x ≤ 230 时,Y = 1050 > 910 9 分…………………………………… 由 7x - 420 ≥ 910 得:x ≥ 190 10 分………………………………………… P(x ≥ 190) = 1 - 0. 01 × 10 = 0. 9 11 分……………………………………… ∴ 估计销售利润不少于 910 万元的概率为 0. 9. 12 分……………………… 20. 解:(1) 抛物线 y2 = 4x 的焦点为 F(1,0) ∴ c = 1 ∵ e = 5 5 　 　 ∴ c a = 5 5 ∴ a = 5 ,b = 2 ∴ 椭圆方程为x2 5 + y2 4 = 1. 3 分………………………………………………… (2) à 当 MN 与 x 轴垂直时,设直线 MN 的方程为:x = t( - 5 < t < 5 ,t ≠ 0) 代入x2 5 + y2 4 = 1 得:M t,2 5 - t2 5 ( ) ,N t, - 2 5 - t2 5 ( ) ∴ k 1 ·k 2 = 2 5 - t2 5t · - 2 5 - t2 5t = - 4 5 ·5 - t2 t2 ∴ - 4 5 ·5 - t2 t2 = - 4 5 　 　 解得:t2 = 5 2 ∴ S △MON = 1 2 t ·4 5 - t2 5 = 5 . 4 分…………………………………… á 当 MN 与 x 轴不垂直时,设 M(x 1 ,y 1 ),N(x 2 ,y 2 ),MN 的方程为 y = kx + m 由 y = kx + m x2 5 + y2 4 = 1 ì î í ïï ïï ⇒(4 + 5k2 )x2 + 10kmx + 5m2 - 20 = 0 5 分…………… 由 △ > 0⇒5k2 + 4 > m2 …………① x 1 + x 2 = - 10km 4 + 5k2 ,x 1 ·x 2 = 5m2 - 20 4 + 5k2 6 分………………………………… )页7共(　　页3第案答)类史文(学数级7102高 ∵ kOM ·kON = - 4 5 　 　 ∴ y 1 x 1 · y 2 x 2 = - 4 5 　 　 ∴ 5y 1 y 2 + 4x 1 x 2 = 0 7 分…… 即(5k2 + 4)x 1 ·x 2 + 5mk(x 1 + x 2 ) + 5m2 = 0 ∴ (5k2 + 4)·5m2 - 20 4 + 5k2 + 5mk· - 10km 4 + 5k2( ) + 5m2 = 0 整理得:2m2 = 5k2 + 4 9 分………………………………………………… 代入 ① 得:m ≠ 0 MN = 1 + k2 (x 1 + x 2 ) 2 - 4x 1 ·x 2 = 1 + k2 · - 10km 4 + 5k2( ) 2 - 4 5m2 - 20 4 + 5k2( ) = 4 5 1 + k2 5k2 + 4 - m2 4 + 5k2 10 分……………………………… O 到 MN 的距离 d = m 1 + k2 11 分………………………………………… ∴ S △MON = 1 2 MN d = 2 5 m 5k2 + 4 - m2 4 + 5k2 = 2 5 m 2m2 - m2 2m2 = 5 综上:S △MON = 5 为定值. 12 分……………………………………………… 21. 解:(1) f(x) 有两个零点 ⇔ 关于 x 的方程 eax = x 有两个相异实根 由 eax > 0,知 x > 0 ∴ f(x) 有两个零点 ⇔ a = lnx x 有两个相异实根. 2 分………………………… 令 G(x) = lnx x ,则 G′(x) = 1 - lnx x2 由 G′(x) > 0 得:0 < x < e ,由 G′(x) < 0 得:x > e ∴ G(x) 在(0,e) 单调递增,在(e, + ∞ ) 单调递减 )页7共(　　页4第案答)类史文(学数级7102高 ∴ G(x) max = G(e) = 1e 3 分…………………………………………………… 又 ∵ G(1) = 0　 　 ∴ 当 0 < x < 1 时,G(x) < 0,当 x > 1 时,G(x) > 0 当 x → + ∞ 时,G(x) → 0 4 分………………………………………………… ∴ f(x) 有两个零点时,实数 a 的取值范围为 0, 1e( ) . 5 分…………………… (2) 由题意得 eax 1 = x 1 eax 2 = x 2 { 　 　 ∴ x 1 > 0,x 2 > 0　 　 ∴ ax 1 = lnx 1 ax 2 = lnx 2 { ∴ a(x 1 + x 2 ) = lnx 1 + lnx 2 ………… ① 　 a(x 2 - x 1 ) = lnx 2 - lnx 1 ∵ x 1 < x 2 ∴ a = lnx 2 - lnx 1 x 2 - x 1 6 分…………………………………………………………… 要证:x 1 ·x 2 > e2 ,只需证 lnx 1 + lnx 2 > 2 由 ① 知:lnx 1 + lnx 2 = a(x 1 + x 2 ) = lnx 2 - lnx 1 x 2 - x 1 ·(x 1 + x 2 ) = x 2 x 1 + 1 x 2 x 1 - 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷·ln x 2 x 1 ∵ 0 < x 1 < x 2 　 　 ∴ x 2 x 1 > 1 令 t = x 2 x 1 ,t > 1 ∴ 只需证 t + 1t - 1 ( )·lnt > 2 7 分………………………………………………… ∵ t > 1　 　 ∴ t + 1t - 1 > 0 ∴ 只需证:lnt > 2(t - 1)t + 1 8 分………………………………………………… 令 F(t) = lnt - 2(t - 1)t + 1 (t > 1) 9 分………………………………………… ∴ F′(t) = 1t - 4 (t + 1) 2 = (t - 1) 2 t(t + 1) 2 > 0 10 分……………………………… ∴ F(t) 在(1, + ∞ ) 递增 )页7共(　　页5第案答)类史文(学数级7102高 ∴ F(t) > F(1) = 0　 　 ∴ lnt > 2(t - 1)t + 1 11 分……………………………… 即 lnx 1 + lnx 2 > 2,即 x 1 ·x 2 > e2 . 12 分……………………………………… 22. 解:(1) 设 M 的极坐标为(ρ,θ),在 △OPM 中,有 ρ = 4sinθ ∴ 点 M 的轨迹的极坐标方程为 ρ = 4sinθ. 4 分……………………………… (2) 设射线 OA:θ = α,α ∈ - π 2 , π 2 ( ) ,圆 C 的极坐标方程为 ρ = 2cosθ 由 ρ = 2cosθ θ = α{ 得: OA = ρ 1 = 2cosα 5 分……………………………………… 由 ρsin θ + π 3 ( ) = 4 θ = α ì î í ïï ïï 得: OB = ρ 2 = 4 sin α + π 3 ( ) 6 分……………………… ∴ OA OB = 2cosα 4 sin α + π 3 ( ) = 1 2 cosα·sin α + π 3 ( ) = 1 2 cosα sinαcos π 3 + cosαsin π 3 ( ) = 1 4 sinαcosα + 3 4 cos 2 α = 1 8 sin2α + 3 8 (cos2α + 1) = 1 4 sin 2α + π 3 ( ) + 3 8 8 分………………………………………… ∵ α ∈ - π 2 , π 2 ( ) 　 　 ∴ - 2π 3 < 2α + π 3 < 4π 3 ∴ 当 2α + π 3 = π 2 ,即 α = π 12 时, OA OB( ) max = 2 + 3 8 9 分………………… ∴ OA OB 的最大值为2 + 3 8 . . 10 分………………………………………… )页7共(　　页6第案答)类史文(学数级7102高 23. 解:(1) f(x) ≤ 4 - 2x - 3 等价于 ì x < - 1 - (x + 1) - (2x - 3) ≤ 4 { 或 í - 1 ≤ x ≤ 3 2 (x + 1) - (2x - 3) ≤ 4 ì î í ïï ïï 或 î x > 3 2 (x + 1) + (2x - 3) ≤ 4 ì î í ïï ïï 由 ì 得: x < - 1 x ≥- 2 3 ì î í ïï ïï ⇒x ∈ Ø 由 í 得: - 1 ≤ x ≤ 3 2 x ≥ 0 ì î í ïï ïï ⇒0 ≤ x ≤ 3 2 由 î 得: x > 3 2 x ≤ 2 ì î í ïï ïï ⇒ 3 2 < x ≤ 2 ∴ 原不等式的解集为 x 0 ≤ x ≤ 2{ } . 5 分…………………………………… (2) ∵ m > 0,n > 0,m + 2n = mn ∴ m + 2n = 1 2 (m·2n) ≤ 1 2 × (m + 2n) 2 4 ∴ m + 2n ≥ 8 7 分……………………………………………………………… 当且仅当 m = 2n m + 2n = mn{ ,即 m = 4 n = 2 { 时取等号 ∴ f(m) + f( - 2n) = m + 1 + - 2n + 1 ≥ m + 2n ≥ 8 9 分……… 当且仅当 - 2n + 1 ≤ 0 即 n ≥ 1 2 时取等号 ∴ f(m) + f( - 2n) ≥ 8. 10 分………………………………………………… )页7共(　　页7第案答)类史文(学数级7102高