2018-2019学年黑龙江省牡丹江市第一高级中学高二寒假开学检测数学（理）试题 Word版

2018-2019学年黑龙江省牡丹江市第一高级中学高二寒假开学检测数学（理）试题 Word版

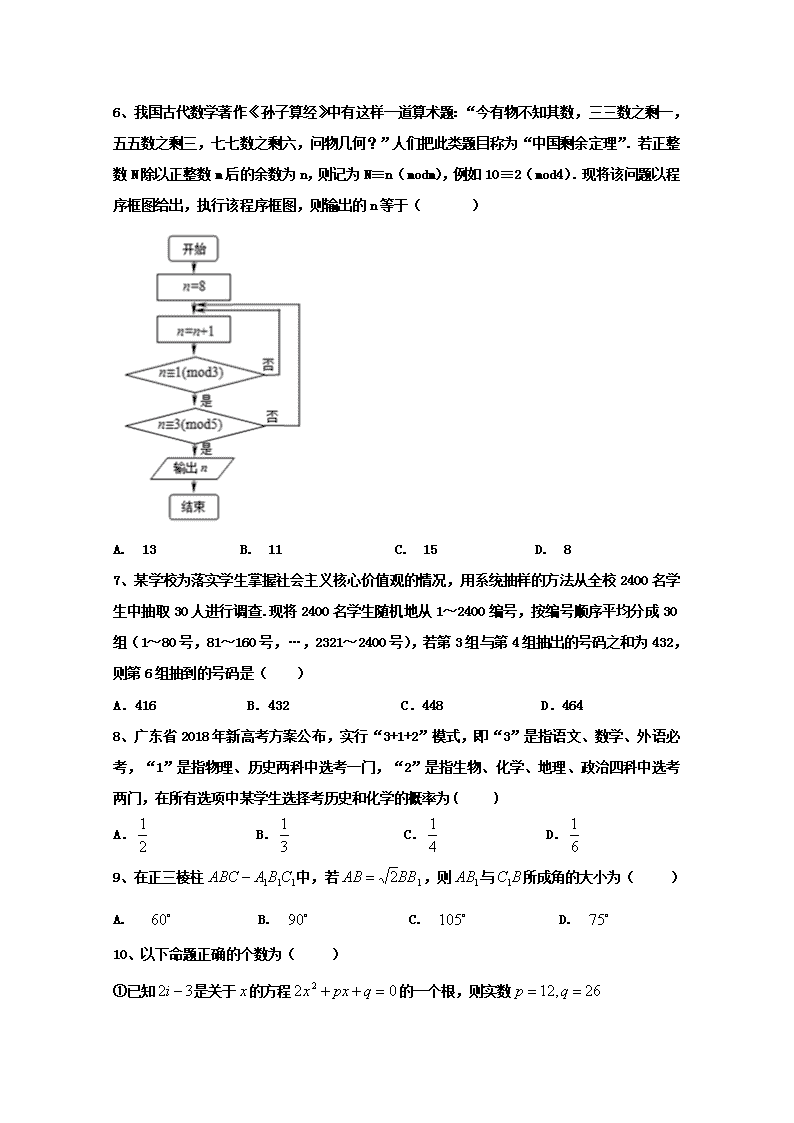
‎2018-2019学年黑龙江省牡丹江市第一高级中学高二寒假开学检测数学（理） 试 题 第Ⅰ卷（选择题） ‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项符合题意的）‎ ‎1、复数的共轭复数是（ ）‎ A. ‎ B. C. D. ‎ ‎2、总体由编号为的50个个体组成，利用随机数表（以下选取了随机数表中的第1行和第2行）选取5个个体，选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取，则选出来的第4个个体的编号为（ ）‎ ‎78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 ‎ ‎32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 ‎ A．05 B．09 C．07 D．20‎ ‎3、已知抛物线，则它的焦点到准线的距离为( ).‎ A. 4 B. 8 C.16 D. 2‎ ‎4、如图是一个边长为4的正方形二维码，为了测算图中黑色部分的面积，在正方形区域内随机投掷400个点，其中落入黑色部分的有225个点，据此可估计黑色部分的面积为（ ） ‎ ‎ ‎ A. ‎11 B. 10 C. 9 D. 8‎ ‎5、已知变量 之间满足线性相关关系 ，且 之间的相关数据如下表所示： ‎ ‎0.1‎ ‎3.1‎ 则 （ ）‎ A. ‎ B. C. D. ‎ ‎6、我国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之剩一，五五数之剩三，七七数之剩六，问物几何？”人们把此类题目称为“中国剩余定理”．若正整数N除以正整数m后的余数为n，则记为N≡n（modm），例如10≡2（mod4）．现将该问题以程序框图给出，执行该程序框图，则输出的n等于（  ） ‎ ‎ ‎ A. 13      B. 11        C. 15       D. 8‎ ‎7、某学校为落实学生掌握社会主义核心价值观的情况，用系统抽样的方法从全校2400名学生中抽取30人进行调查.现将2400名学生随机地从1～2400编号，按编号顺序平均分成30组（1～80号，81～160号，…，2321～2400号），若第3组与第4组抽出的号码之和为432，则第6组抽到的号码是（ ）‎ A．416 B．432 C．448 D．464‎ ‎8、广东省2018年新高考方案公布，实行“3+1+2”模式，即“3”是指语文、数学、外语必考，“1”是指物理、历史两科中选考一门，“2”是指生物、化学、地理、政治四科中选考两门，在所有选项中某学生选择考历史和化学的概率为( )‎ A． B． C． D．‎ ‎9、在正三棱柱中，若，则与所成角的大小为（ ）‎ A. ‎ B. C. D. ‎ ‎10、以下命题正确的个数为（ ）‎ ‎①已知是关于的方程的一个根，则实数 ‎②分别是四面体的棱的中点，是线段的靠近点的三等分点，则 ‎③如果点在运动过程中，总满足关系式，则点的轨迹是双曲线。‎ ‎④若集合，则集合的不同子集个数为64个。‎ ‎⑤某小组有3名男生和2名女生，从中任选 2名学生参加演讲比赛，则恰有1名男生和恰有2名男生为对立事件。‎ A. ‎ 1个 B. 2个 C. 3个 D. 4个 ‎11、《中国诗词大会》（第二季）亮点颇多，十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下，百人团齐声朗诵，别有韵味．若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场，且《将进酒》排在《望岳》的前面，《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后，则后六场的排法有（ ）‎ A．288种 B．144种 C．720种 D．360种 ‎12、已知椭圆的右焦点为，且离心率为，的三个顶点都在椭圆上，设三条边的中点分别为点，且三条边所在直线的斜率分别为，且均不为0，为坐标原点，若直线的斜率之和为1，则的值为（ ）‎ A. B. C. D. ‎ 第Ⅱ卷（非选择题共90分）‎ 二、 填空题（本大题共4小题，每题5分，满分20分．）‎ ‎13、已知三个数12(16) ，25(7) ，33(4) ，则将它们按由小到大的顺序排列为________． ‎ ‎14、用数字组成没有重复数字的四位偶数有 个。‎ ‎15、甲、乙两艘轮船都要在某个泊位停靠6小时，假定它们在一昼夜的时间段中随机地到达，则这两艘船中至少有一艘在停靠泊位时必须等待的概率为 ‎ ‎16、已知双曲线的右焦点为，过的直线交双曲线的渐近线于两点，且直线的倾斜角是渐近线倾斜角的2倍，若则该双曲线的离心率为__________.‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤.‎ ‎17、（10分）在直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求直线的普通方程及曲线的直角坐标方程；‎ ‎（2）求曲线上的点到的距离的最大值.‎ ‎18、某大学为调查来自南方和北方的同龄大学生的身高差异，从2016级的年龄在18～19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名，测量他们的身高，量出的身高如下(单位：cm)：‎ 南方：158，170，166，169，180，175，171，176， 162，163.‎ 北方：183，173，169，163，179，171，157，175，184，166.‎ （1） 根据抽测结果，画出茎叶图，对来自南方和北方的大学生的身高作比较，写出统计结论． （2）设抽测的10名南方大学生的平均身高为169 cm，将10名南方大学生的身高依次输入如图所示 的 程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义。 ‎ ‎19、某高校数学与统计学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名，对他们在2018年高考的数学成绩进行调查，统计发现40名新生的数学分数分布在内.当时，其频率.‎ ‎（1）求的值；‎ ‎（2）请在答题卡中画出这40名新生高考数学分数的频率分布直方图，并估计这40名新生的高考数学分数的平均数；‎ ‎（3）从成绩在100～120分的学生中，用分层抽样的方法从中抽取5名学生，再从这5名学生中随机选两人甲、乙，记甲、乙的成绩分别为，求概率．‎ ‎20、在四棱锥中，侧面底面，底面为直角梯形，为的中点，为的中点。‎ ‎（1）求证：∥平面；‎ ‎（2）求二面角的余弦值。‎ ‎21、‎ 近年来，随着我国汽车消费水平的提高，二手车流通行业得到迅猛发展．某汽车交易市场对2017年成交的二手车交易前的使用时间（以下简称“使用时间”）进行统计，得到频率分布直方图如图1．    图1                     图2 附注：①对于一组数据 ，其回归直线 的斜率和截距的最小二乘估计分别为， ； ②参考数据： ． ‎ ‎（1）记“在年成交的二手车中随机选取一辆，该车的使用年限在 ”为事件，试估计的概率； ‎ ‎（2）根据该汽车交易市场的历史资料，得到散点图如图2，其中(单位：年)表示二手车的使用时间， (单位：万元)表示相应的二手车的平均交易价格．由散点图看出，可采用 作为二手车平均交易价格关于其使用年限的回归方程，相关数据如下（其中 ，）：‎ ‎ 根据回归方程类型及表中数据，建立关于的回归方程。 22、设椭圆的离心率为，左顶点到直线的距离为．‎ ‎（1）求椭圆的方程；‎ ‎（2）设直线与椭圆相交于两点，若以为直径的圆经过坐标原点，试探究：点到直线的距离是否为定值？若是，求出这个定值；否则，请说明理由；‎ ‎（3）在（2）的条件下，试求面积的最小值．‎ 数学（理）答案 选择 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C A C B A A C B C B B 填空 ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 c

查看更多