2019-2020学年江西省宜春市上高二中高二上学期第三次月考数学（文）试题 Word版

2019-2020学年江西省宜春市上高二中高二上学期第三次月考数学（文）试题 Word版

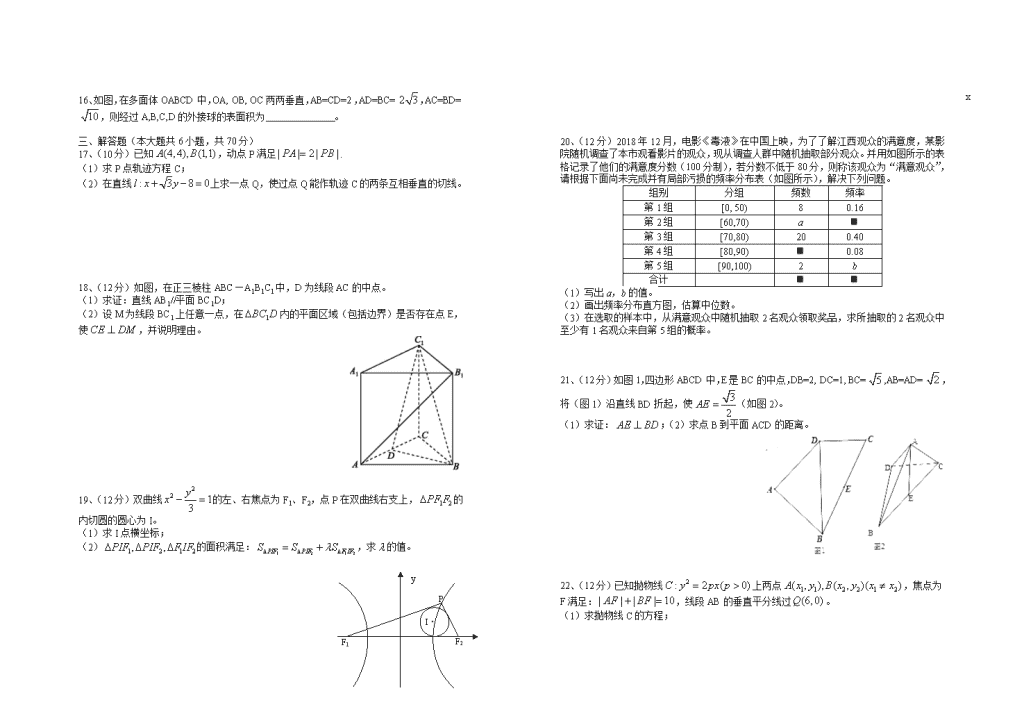
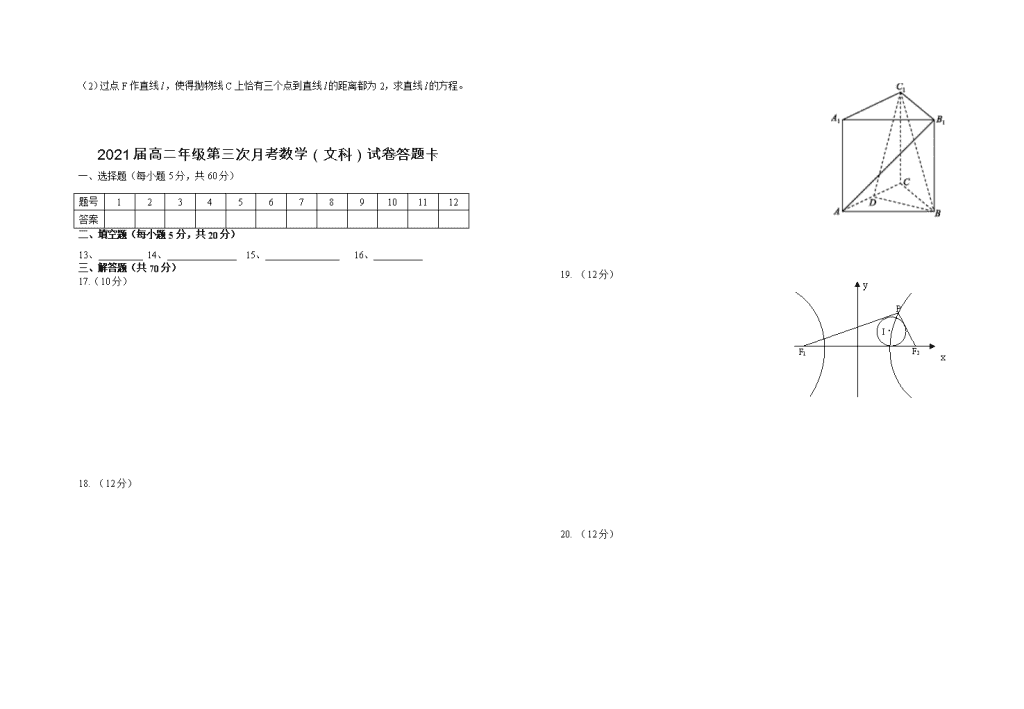
江西省宜春市上高二中2019-2020学年高二上学期第三次月考数学（文科）试卷 命题：黄勋全 12.22‎ 一、选择题（每小题5分，共60分）‎ ‎1、在空间直角坐标系中，点与两点的位置关系是（ ）‎ A．关于x轴对称 B．关于xOy平面对称 ‎ C．关于坐标原点对称 D．以上都不对 ‎2、设m，n是两条不同的直线，是两个不同的平面，下列命题中正确的是（ ）‎ A．若则 ‎ B．若则 C．若则 ‎ D．若则 ‎3、如图，的斜二测直观图为等腰，其中=2，则原的面积为（ ）‎ A．2 B．4 C． D． ‎ ‎4、椭圆左、右顶点为A、B，P是椭圆C上一点，最小值为，则双曲线：的渐近线方程为（ ）‎ A． B． C． D．‎ ‎5、如果数据的平均值为5，方差为16，则数据：的平均值和方差分别为（ ）‎ A．-1，36 B．-1，41 C．1，72 D．-10，144‎ ‎6、已知变量x与y负相关，且由观测数据算得样本平均数，则由该观测数据算得的线性回归方程可能是（ ）‎ A． B．‎ C． D．‎ ‎7、直线与双曲线的右支交于不同的两点，那么的取值范围是（ ）‎ A． B． C． D．‎ ‎8、某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛，他们取得的成绩（满分100）的茎叶图如图所示，其中甲班学生成绩的平均分为86，乙班学生成绩的中位数是83，则的值为（ ）‎ A．9 B．10 C．11 D．13‎ ‎9、某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大值为（ ）‎ A． B． C． D． ‎ ‎10、在正方体中，动点P在侧面上运动，若P点到直线AB的距离等于P点到平面的距离，则P点轨迹类型是（ ）‎ A．直线 B．圆 C．抛物线 D．椭圆 ‎11、已知椭圆与圆，若在椭圆上存在点P，过P作圆的切线PA，PB，切点为A，B使得，则椭圆的离心率的取值范围是（ ）‎ A． B． C． D．‎ ‎12、数学中有许多形状优美、寓意美好的曲线，曲线C：就是其中之一（如图）．给出下列三个结论：‎ ‎①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；‎ ‎②曲线C上任意一点到原点的距离都不超过；‎ ‎③曲线C所围成的“心形”区域的面积小于3．‎ 其中所有正确结论的序号是 A．① B．② C．①② D．①②③‎ 二、填空题（每小题5分，共20分）‎ ‎13、抛物线的焦点坐标为 ‎ A B C C1‎ B1‎ A1‎ E D ‎14、设P是双曲线上一点，M、N分别是两圆：和上的点，则的最大值为 ‎ ‎15、正三棱柱的棱长都为2，D、E分别是AB、A1C1的中点，则异面直线B1C与DE所成角余弦值为 ‎ ‎16、如图，在多面体OABCD中，OA, OB, OC两两垂直，AB=CD=2，AD=BC=，AC=BD=，则经过A,B,C,D的外接球的表面积为 。‎ 三、解答题（本大题共6小题，共70分）‎ ‎17、（10分）已知，动点P满足.‎ ‎（1）求P点轨迹方程C；‎ ‎（2）在直线上求一点Q，使过点Q能作轨迹C的两条互相垂直的切线。‎ ‎18、（12分）如图，在正三棱柱ABC—A1B1C1中，D为线段AC的中点。‎ ‎（1）求证：直线AB1//平面BC1D；‎ ‎（2）设M为线段BC1上任意一点，在内的平面区域（包括边界）是否存在点E，使，并说明理由。‎ ‎19、（12分）双曲线的左、右焦点为F1、F2，点P在双曲线右支上，的内切圆的圆心为I。‎ ‎（1）求I点横坐标；‎ ‎（2）的面积满足：，求的值。‎ y P I·‎ F1‎ F2‎ x ‎20、（12分）2018年12月，电影《毒液》在中国上映，为了了解江西观众的满意度，某影院随机调查了本市观看影片的观众，现从调查人群中随机抽取部分观众。并用如图所示的表格记录了他们的满意度分数（100分制），若分数不低于80分，则称该观众为“满意观众”，‎ 请根据下面尚未完成并有局部污损的频率分布表（如图所示），解决下列问题。‎ 组别 分组 频数 频率 第1组 ‎[0, 50)‎ ‎8‎ ‎0.16‎ 第2组 ‎[60,70)‎ a 第3组 ‎[70,80)‎ ‎20‎ ‎0.40‎ 第4组 ‎[80,90)‎ ‎0.08‎ 第5组 ‎[90,100)‎ ‎2‎ b 合计 ‎（1）写出a，b的值。‎ ‎（2）画出频率分布直方图，估算中位数。‎ ‎（3）在选取的样本中，从满意观众中随机抽取2名观众领取奖品，求所抽取的2名观众中至少有1名观众来自第5组的概率。‎ ‎21、（12分）如图1，四边形ABCD中，E是BC的中点，DB=2, DC=1, BC=,AB=AD=，将（图1）沿直线BD折起，使（如图2）。‎ ‎（1）求证：；（2）求点B到平面ACD的距离。‎ ‎22、（12分）已知抛物线上两点，焦点为F满足：，线段AB的垂直平分线过。‎ ‎（1）求抛物线C的方程；‎ ‎（2）过点F作直线，使得抛物线C上恰有三个点到直线的距离都为2，求直线的方程。‎ ‎2021届高二年级第三次月考数学（文科）试卷答题卡 一、选择题（每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二、填空题（每小题5分，共20分）‎ ‎13、 14、 15、 16、 ‎ 三、解答题（共70分）‎ ‎17.（10分）‎ ‎18. （12分）‎ y ‎19. （12分）‎ P I·‎ F1‎ F2‎ x ‎20. （12分）‎ ‎21. （12分）‎ ‎22.（12分）‎ ‎2021届高二年级第三次月考数学（文科）试卷答案 题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 A D D B A D C D B C A C ‎13. 14. 9 15. 16. ‎ ‎19. ‎ P B I·‎ A F1‎ F2‎ C ‎20. ‎ ‎50 ‎ ‎100 分数 ‎60 ‎ ‎70 ‎ ‎80 ‎ ‎90 ‎ ‎0.004‎ ‎0.008‎ ‎0.016‎ ‎0.032‎ ‎0.046‎ ‎21、（1）取BD中点为F，连结AF，EF，则EF=‎ ‎（2）‎ ‎22. （1）‎ ‎（2）‎