2017届高考数学(文)(新课标)二轮专题复习(检测) 第三部分 专题四 概率、统计 作业22-23
概率与统计专练(一)·作业(二十二)
1.(2016·河北衡水中学三模)随机抽取某中学高三年级甲、乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图,其中甲班有一个数据被污损.
(1)若已知甲班同学身高平均数为170 cm,求被污损的数据;
(2)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
解析 (1)设甲班未知的数据为a,
由==170,
解得a=179,所以被污损的数据是9.
(2)设“身高为176 cm的同学被抽中”为事件A,
从乙班10名同学中随机抽取两名身高不低于173 cm的同学,基本事件有(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178,176),(176,173),共10个,
而事件A包含的基本事件有(181,176),(179,176),(178,176),(176,173),共4个,
所以P(A)==.
答:身高为176 cm的同学被抽中的概率为.
2.(2016·广东肇庆第三次模拟)某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
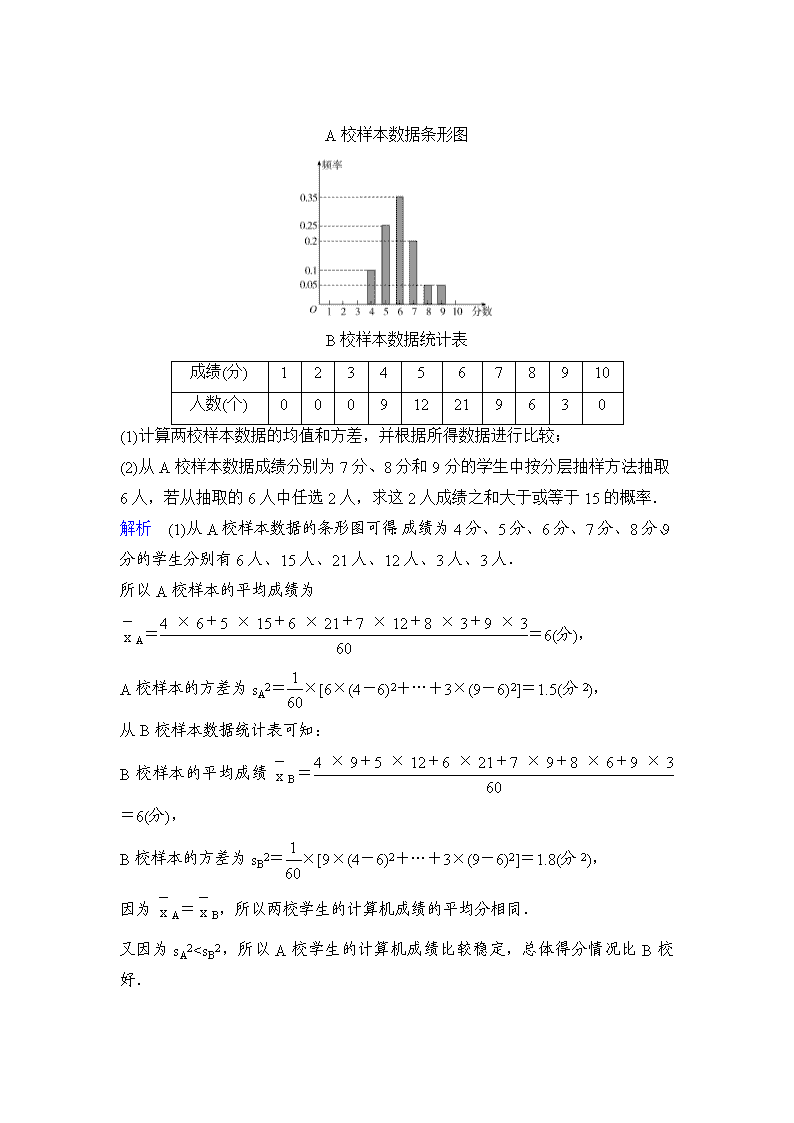
A校样本数据条形图
B校样本数据统计表
成绩(分)
1
2
3
4
5
6
7
8
9
10
人数(个)
0
0
0
9
12
21
9
6
3
0
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较;
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人,求这2人成绩之和大于或等于15的概率.
解析 (1)从A校样本数据的条形图可得:成绩为4分、5分、6分、7分、8分、9分的学生分别有6人、15人、21人、12人、3人、3人.
所以A校样本的平均成绩为
A==6(分),
A校样本的方差为sA2=×[6×(4-6)2+…+3×(9-6)2]=1.5(分2),
从B校样本数据统计表可知:
B校样本的平均成绩B==6(分),
B校样本的方差为sB2=×[9×(4-6)2+…+3×(9-6)2]=1.8(分2),
因为A=B,所以两校学生的计算机成绩的平均分相同.
又因为sA2
3.841.
所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
概率与统计专练(二)·作业(二十三)
1.(2016·西安检测)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.
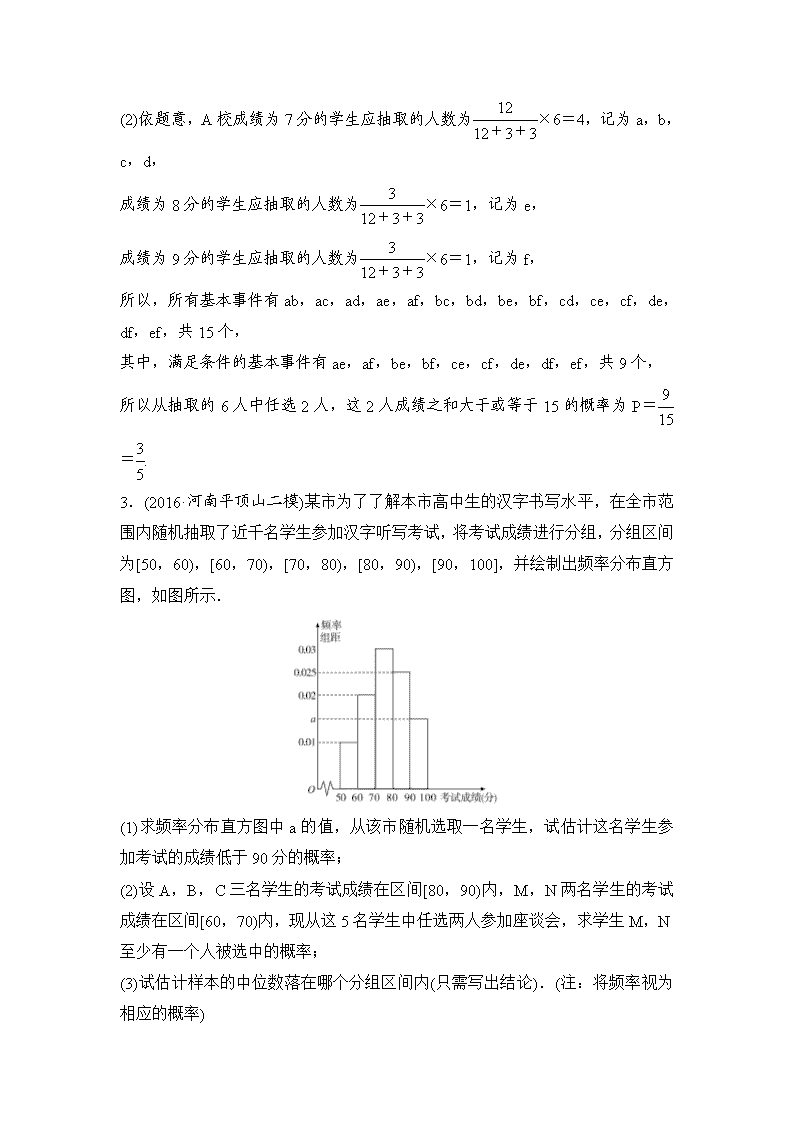
(1)求图中a的值;
(2)求甲队员命中环数大于7的概率(频率当作概率使用);
(3)由图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不要求证明).
解析 (1)由图可得0.01+a+0.19+0.29+0.45=1,
所以a=0.06.
(2)设事件A为“甲队员命中环数大于7”,它包含三个两两互斥的事件:命中环数为8,9,10,
所以P(A)=0.29+0.45+0.01=0.75.
(3)甲队员的射击成绩更稳定.
2.(2016·邯郸一模)在某大学联盟的自主招生考试中,报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如图所示,本次考试中成绩在[90,100]内的记为A,其中“语文”科目成绩在[80,90)内的考生有10人.
(1)求该考场考生数学科目成绩为A的人数;
(2)已知在本考场参加考试的考生中,恰有2人的两科成绩均为A,在至少一科成绩为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为A的概率.
解析 (1)该考场的考生人数为10÷0.25=40.
数学科目成绩为A的人数为40×(1-0.002 5×10-0.015×10-0.037 5×10×2)=40×0.075=3.
(2)语文和数学成绩为A的各有3人,其中有两人的两科成绩均为A,所以还有两名同学只有一科成绩为A.
设这四人为甲、乙、丙、丁,其中甲、乙的两科成绩均为A,则在至少一科成绩为A的考生中,随机抽取两人进行访谈,基本事件为{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁},共6个.
设“随机抽取2人,这2人的两科成绩均为A”为事件M,则事件M包含的事件有1个,则P(M)=.
3.(2016·福建基地综合)某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求日利润y(单位:元)关于日需求量n(单位:件,n∈N)的函数解析式;
(2)商店记录了50天该商品的日需求量n(单位:件),整理得下表:
日需求量n
8
9
10
11
12
频数
9
11
15
10
5
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求日利润在区间[400,550]内的概率.
解析 (1)当日需求量n≥10时,日利润为y=50×10+(n-10)×30=30n+200,
当日需求量n<10时,利润y=50×n-(10-n)×10=60n-100.
所以日利润y与日需求量n的函数解析式为y=
(2)50天内有9天获得的日利润为380元,有11天获得的日利润为440元,有15天获得日利润为500元,有10天获得的日利润为530元,
有5天获得的日利润为560元.
所以
①这50天的日利润(单位:元)的平均数为=477.2.
②日利润(单位:元)在区间[400,550]内的概率为P==.
4.(2016·江南十校联考)第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届
伦敦
第29届
北京
第28届
雅典
第27届
悉尼
第26届
亚特兰大
中国
38
51
32
28
16
俄罗斯
24
23
27
32
26
(1)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可).
(2)下表是近五届奥运会中国代表团获得的金牌数之和,(从第26届算起,不包括之前已获得的金牌数)随时间x变化的数据:
时间x/届
26
27
28
29
30
金牌数之和y/枚
16
44
76
127
165
作出散点图如下:
①由图可以看出,金牌数之和y与时间x之间存在线性相关关系,请求出y关于x的线性回归方程;
②利用①中的回归方程,预测今年中国代表团获得的金牌数.
参考数据:=28,=85.6, (xi-)(yi-)=381,
(xi-)2=10.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线=+t中斜率和截距的最小二乘估计公式分别为:=,=- .
解析 (1)两国代表团获得的金牌数的茎叶图如下:通过茎叶图可以看出,中国代表团获得的金牌数的平均值高于俄罗斯代表团获得的金牌数的平均值;俄罗斯代表团获得的金牌数比较集中,中国代表团获得的金牌数比较分散.
(2)①===38.1,
=- =85.6-38.1×28=-981.2,
所以金牌数之和y关于时间x的线性回归方程为
=38.1x-981.2.
②由①知,当x=31时,中国代表团获得的金牌数之和的预报值=38.1×31-981.2=199.9,
故预测今年中国代表团获得的金牌数为
199.9-165=34.9≈35(枚).
1.某班甲、乙两名学同参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
1
2
3
4
5
6
7
8
9
10
甲
11.6
12.2
13.2
13.9
14.0
11.5
13.1
14.5
11.7
14.3
乙
12.3
13.3
14.3
11.7
12.0
12.8
13.2
13.8
14.1
12.5
(1)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(2)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
解析 (1)茎叶图
从统计图中可以看出,乙的成绩较为集中,差异程度较小,应选派乙同学代表班级参加比赛较好.
(2)设甲同学的成绩为x,乙同学的成绩为y,
则|x-y|<0.8,
得-0.8+x
查看更多