- 2021-06-17 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年中考数学提分训练 不等式与不等式组(含解析) 新版新人教版
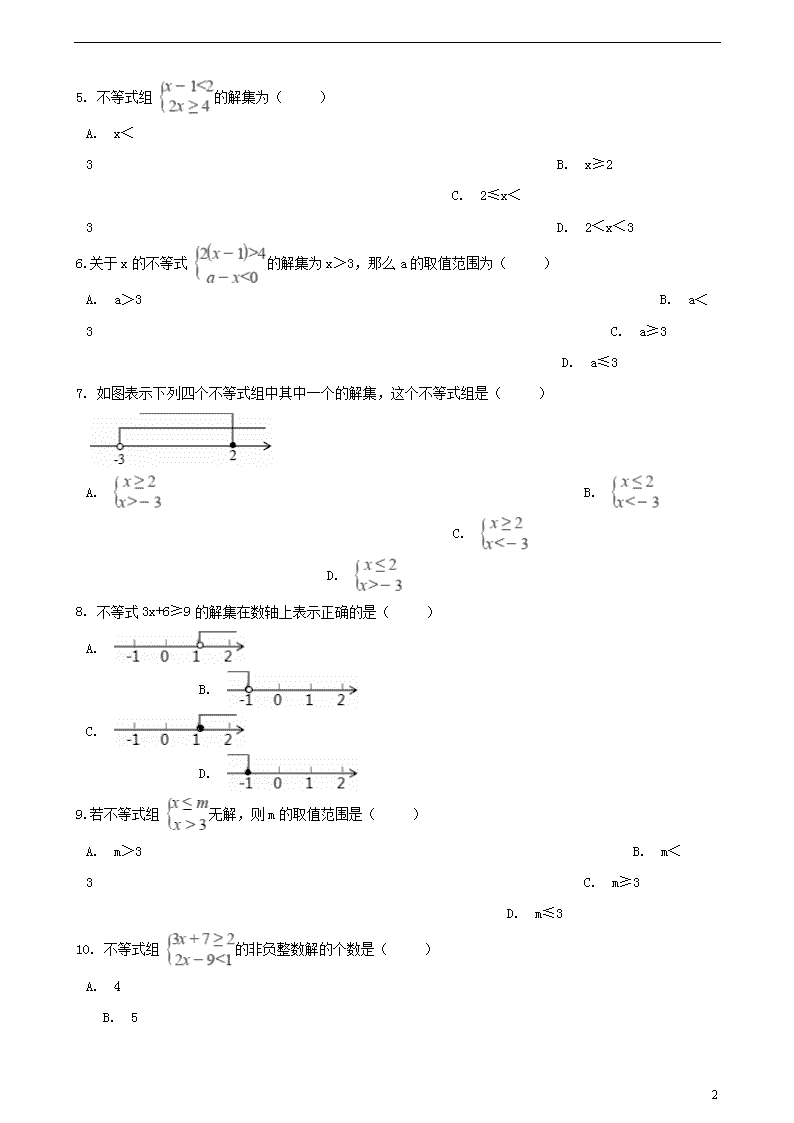
2019年中考数学提分训练: 不等式与不等式组 一、选择题 1.不等式组 的解集为( ) A. x> B. x>1 C. <x<1 D. 空集 2.下列哪个选项中的不等式与不等式 组成的不等式组的解集为 .( ) A. B. C. D. 3.如图的宣传单为莱克印刷公司设计与印刷卡片计价方式的说明,妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的2成?( ) A. 112 B. 121 C. 134 D. 143 4.不等式组 的解集在数轴上表示正确的是( ) A. B. C. D. 11 5. 不等式组 的解集为( ) A. x<3 B. x≥2 C. 2≤x<3 D. 2<x<3 6.关于x的不等式 的解集为x>3,那么a的取值范围为( ) A. a>3 B. a<3 C. a≥3 D. a≤3 7. 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( ) A. B. C. D. 8. 不等式3x+6≥9的解集在数轴上表示正确的是( ) A. B. C. D. 9.若不等式组 无解,则m的取值范围是( ) A. m>3 B. m<3 C. m≥3 D. m≤3 10. 不等式组 的非负整数解的个数是( ) 11 A. 4 B. 5 C. 6 D. 7 二、填空题 11. 不等式2x+1>0的解集是________. 12. 已知“x的3倍大于5,且x的一半与1的差不大于2”,则x的取值范围是________. 13.不等式组 的解集是________. 14.不等式组 的最小整数解是________. 15.若不等式组 的解集是x>3,则m的取值范围是________. 16.如果关于x的方程x2﹣3x+m=0没有实数根,那么m的取值范围是________. 17. 不等式组 的解集是x>﹣1,则a的取值范围是________. 18.用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 ________, ________, ________. 三、解答题 19.计算题 (1)解不等式2x+9≥3(x+2) (2)解不等式组 并写出其整数解。 (3)已知二元一次方程组 的解x、y均是正数, ①求a的取值范围; ②化简|4a+5|-|a-4|. 11 20.深圳某居民小区计划对小区内的绿化进行升级改造,计划种植A , B两种观赏盆栽植物700盆.其中A种盆栽每盆16元,B种盆栽每盆20元.相关资料表明:A , B两种盆栽的成活率分别为93%和98%. (1)若购买这两种盆栽共用11600元,则A , B两种盆栽各购买了多少盆? (2)要使这批盆栽的成活率不低于95%,则A种盆栽最多可购买多少盆? (3)在(2)的条件下,应如何选购A , B两种盆栽,使购买盆栽的费用最低,此时最低费用为多少? 21.某商场计划购进 、 两种型号的手机,已知每部 型号手机的进价比每部 型号手机的多500元,每部 型号手机的售价是2500元,每部 型号手机的售价是2100元. (1)若商场用50000元共购进 型号手机10部, 型号手机20部.求 、 两种型号的手机每部进价各是多少元? (2)为了满足市场需求,商场决定用不超过7.5万元采购 、 两种型号的手机共40部,且 型号手机的数量不少于 型号手机数量的2倍.①该商场有哪几种进货方式? ②该商场选择哪种进货方式,获得的利润最大? 11 参考答案 一、选择题 1.【答案】B 【解析】 解不等式2x>1-x,得:x> , 解不等式x+2<4x-1,得:x>1, 则不等式组的解集为x>1, 故答案为:B. 【分析】分别解出不等式组中的每一个不等式的解集,然后根据同大取大即可得出答案。 2.【答案】C 【解析】 :5x>8+2x, 解得:x> , 根据大小小大中间找可得另一个不等式的解集一定是x<5, 故答案为:C. 【分析】解出题干中的不等式的解集,再根据不等式组的解集,由大小小大中间找可得另一个不等式的解集,然后把四个答案中的每一个不等式解出,即可得出答案。 3.【答案】C 【解析】 :设妮娜需印x张卡片, 根据题意得:15x﹣1000﹣5x>0.2(1000+5x), 解得:x>133 , ∵x为整数, ∴x≥134. 【分析】由题意可得不等关系;销售总额-设计费-所有卡片印刷费02(设计费-所有卡片的印刷费),根据不等关系列出不等式,并解不等式即可求解。 4.【答案】B 【解析】 :由①得:x>-2 由②得:x≤2 此不等式组的解集为:-2<x≤2 11 在数轴上表示为: 故答案为:B【分析】先求出不等式组中的每一个不等式的解集,再根据不等式组的解集的确定方法,求出其解集,然后在数轴上表示,即可得出结果。 5.【答案】C 【解析】 : ∵解不等式①得:x<3, 解不等式②得:x≥2, ∴不等式组的解集为2≤x<3, 故选C. 【分析】先求出每个不等式的解集,再求出不等式组的解集即可. 6.【答案】D 【解析】 :解不等式2(x-1)>4,得:x>3, 解不等式a-x<0,得:x>a, ∵不等式组的解集为x>3, ∴a≤3, 故答案为:D. 【分析】分别解出不等式组中的每一个不等式,然后根据题干知不等式组的解集为x>3,根据同大取大的法则即可得出a≤3。 7.【答案】D 【解析】 :∵﹣3处是空心圆点,且折线向右,2处是实心圆点,且折线向左, ∴这个不等式组的解集是﹣3<x≤2. 故选D. 【分析】根据在数轴上表示不等式解集的方法即可得出答案. 8.【答案】C 【解析】 :移项,得:3x≥9﹣6, 合并同类项,得:3x≥3, 系数化为1,得:x≥1, 故选:C 【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得. 9.【答案】D 11 【解析】 ∵不等式组 无解, ∴m≤3.故答案为:D. 【分析】根据大大小小无处找,即可得出m的取值范围。 10.【答案】B 【解析】 : ∵解不等式①得:x≥﹣ , 解不等式②得:x<5, ∴不等式组的解集为﹣ ≤x<5, ∴不等式组的非负整数解为0,1,2,3,4,共5个, 故选B. 【分析】先求出不等式组的解集,再求出不等式组的非负整数解,即可得出答案. 二、填空题 11.【答案】x>﹣ 【解析】 :原不等式移项得, 2x>﹣1, 系数化1得, x>﹣ . 故本题的解集为x>﹣ . 【分析】利用不等式的基本性质,将两边不等式同时减去1再除以2,不等号的方向不变;即可得到不等式的解集. 12.【答案】<x≤6 【解析】 :依题意有 , 解得 <x≤6. 故x的取值范围是 <x≤6. 故答案为: <x≤6. 【分析】根据题意列出不等式组,再求解集即可得到x的取值范围. 13.【答案】x<3 【解析】 : 由(1)得,x<4, 11 由(2)得,x<3, 所以不等式组的解集为:x<3. 故答案为:x<3. 【分析】分别解出不等式组中每一个不等式的解集,然后根据同小取小,即可得出不等式组的解集。 14.【答案】0 【解析】 : , 解①得x>﹣1, 解②得x≤3, 不等式组的解集为﹣1<x≤3, 不等式组的最小整数解为0, 故答案为0. 【分析】先解不等式组,求出解集,再找出最小的整数解即可. 15.【答案】m≤3 【解析】 :∵不等式组 的解集是x>3, ∴m≤3. 故答案为:m≤3. 【分析】根据“同大取较大”的法则进行解答即可. 16.【答案】m> 【解析】 :∵关于x的方程x2﹣3x+m=0没有实数根, ∴b2﹣4ac=(﹣3)2﹣4×1×m<0, 解得:m> , 故答案为:m> . 【分析】根据根的判别式得出b2﹣4ac<0,代入求出不等式的解集即可得到答案. 17.【答案】a≤﹣ 【解析】 :解不等式x+1>0,得:x>﹣1, 解不等式a﹣ x<0,得:x>3a, ∵不等式组的解集为x>﹣1, 则3a≤﹣1, ∴a≤﹣ , 故答案为:a≤﹣ . 11 【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了,结合不等式组的解集即可确定a的范围. 18.【答案】2;3;-1 【解析】 :根据不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变. 满足 , 即可,例如: ,3, . 故答案为: ,3, . 【分析】此题是一道开放性的命题,根据不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.故所写答案只要满足 a < b , c ≤ 0 即可, 三、解答题 19.【答案】(1)解:2x+9≥3x+6 2x-3x≥6-9 x≤3 (2)解:由①得 x<2 由②得 2x>-1 x>- ∴此不等式组的解集为:-<x<2 它的整数解为:0、1 (3)解:①由①+②得:2x=8a+10 解之:x=4a+5 由①-②得:2y=-2a+8 解之:y=-a+4 ∴方程组的解为: ∵原方程组的解x、y均是正数, ∴ 解之: ②∵4a+5>0且a-4<0 ∴|4a+5|-|a-4|=4a+5-(4-a)=5a+1 【解析】【分析】(1)先去括号,再移项合并同类项,把x的系数化为1,即可求解。 (2 11 )先求出不等式组中的每一个不等式的解集,再确定不等式组的解集,然后求出不等式组的整数解即可。 (3)①先解方程组,再根据x>0,y>0,解关于a的不等式组,即可得出a的取值范围;②根据a的取值范围,化简即可。 20.【答案】(1)解 :设购买A种盆栽x盆,则购买B种盆栽y盆 由题意得: 解得: 故购买A种盆栽600盆,则购买B种盆栽100盆。 (2)解 :设可购A种盆栽为a盆( ),则购买B种盆栽(700-a)盆 由题意得: 解得: ,所以A种盆栽最多可购买420盆。 (3)解 :设可购A种盆栽为b盆,购买盆栽的总费用S,根据题意得出 由(2)可知 ,当b=420时,总费用最低,此时s=12320 此时购买B种盆栽:700-420=280(盆) 故购买A种盆栽420盆,则购买B种盆栽280盆时,购买费用最低,最低费用为12320元。 【解析】【分析】(1)设购买A种盆栽x盆,则购买B种盆栽y盆,根据计划种植A , B两种观赏盆栽植物700盆,及购买这两种盆栽共用11600元,列出二元一次方程组,求解即可; (2)设可购A种盆栽为a盆( 0 ≤ a ≤ 700 ),则购买B种盆栽(700-a)盆,根据A种树苗成活的数量+B种树苗成活的数量的和除以700得出这批树苗的成活率,根据这批盆栽的成活率不低于95%,列出不等式,求解即可得出答案; (3)设可购A种盆栽为b盆,购买盆栽的总费用S, 从而列出函数关系式, s = 16 b + 20 ( 700 − b ) = 14000 − 4 b,根据一次函数的性质得出 由(2)可知 b ≤ 420 ,当x=420时,总费用最低,此时s=12320,进而得出购买方案。 21.【答案】(1)解:A型号的手机每部进价为x元,B型号的手机每部进价为y元,根据题意得 解之: (2)解:设购进A型号的手机m部,则购进B型号的手机(40-m)部则: 解之: 11 ∵m为正整数 ∴m=27、28、29、30 ∴该商场一共有5种进货方案; ②设总利润为W ∴W=(2500-2000)m+(2100-1500)(40-m)=-100m+24000 ∵k=-100<0, ∴W随m的增大而减小 ∴m取最小值为27时,W最大值=-2700+24000=21300元 【解析】【分析】(1)根据题意可得等量关系:A型号手机额单价-B型号手机的单价=500;10部A型号手机的总价+20部B型号手机的总价=50000;列方程组求解即可。 (2)①商场决定用不超过7.5万元采购、两种型号的手机共40部,且型号手机的数量不少于型号手机数量的2倍,设未知数,建立不等式组,求出其整数解即可解答;②设总利润为W,建立W关于m的函数解析式,再根据一次函数的性质,即可求解。 11查看更多