数学（理）（火箭班）卷·2019届河南省林州市第一中学高二3月调研考试（2018-03）

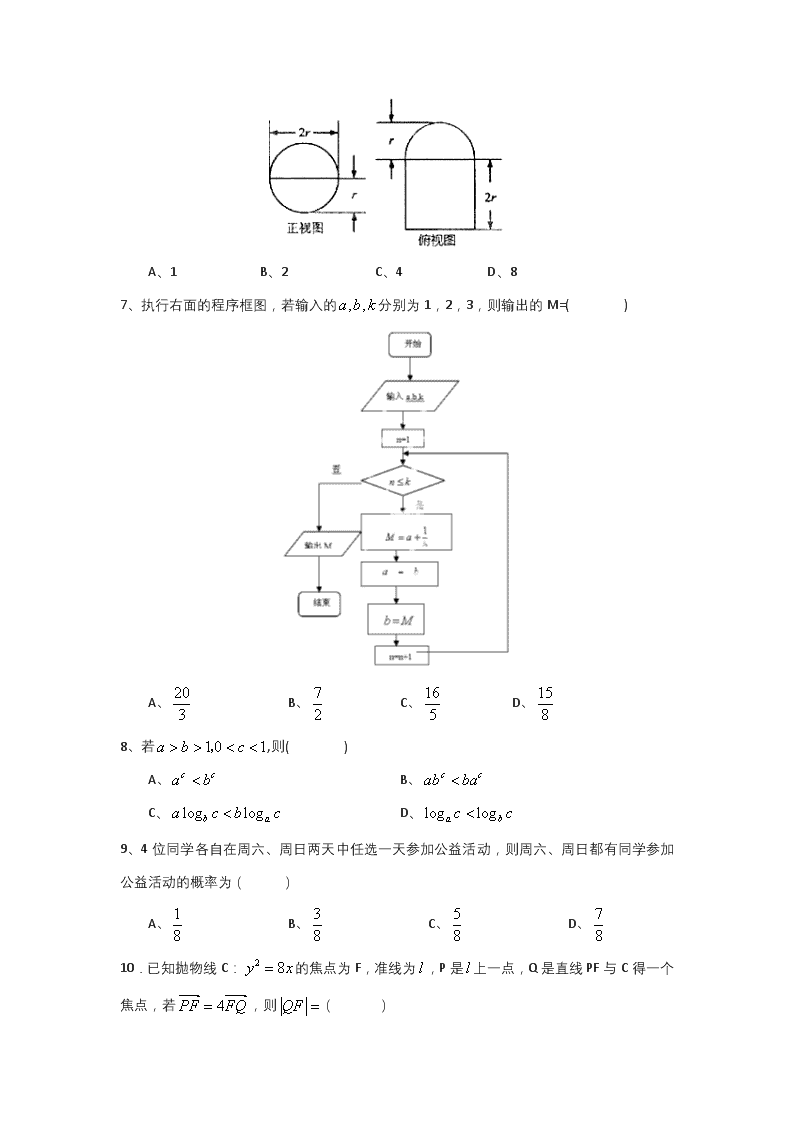
数学（理）（火箭班）卷·2019届河南省林州市第一中学高二3月调研考试（2018-03）

‎2016级高二火箭班3月调研考试 数学（理）试题 一、选择题（每题5分）‎ ‎1、已知集合A=｛x|x2－2x＞0｝，B=｛x|－＜x＜｝，则( )‎ A、A∩B=Æ B、AB=R C、BA D、AB ‎2、若复数z满足 (3－4i)z＝|4＋3i |，则z的虚部为 ( )‎ A、－4 B、－ C、4 D、 ‎3、投篮测试中，每人投3次，至少投中2次才能通过测试。已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为( )‎ A、0.648 B、0.432 C、0.36 D、0.312‎ ‎4、已知为双曲线:的一个焦点，则点到的一条渐近线的距离为( )‎ A、 B、3 C、 D、‎ ‎5、函数=的部分图像如图所示，则的单调递减区间为( )‎ A、 B、‎ C、 D、 ‎ ‎6、圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20，则r=( )‎ A、1 B、2 C、4 D、8‎ ‎7、执行右面的程序框图，若输入的分别为1，2，3，则输出的M=( )‎ A、 B、 C、 D、‎ ‎8、若,则( )‎ A、 B、 ‎ C、 D、‎ ‎9、4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率为（ ）‎ A、 B、 C、 D、‎ ‎10．已知抛物线C：的焦点为F，准线为，P是上一点，Q是直线PF与C得一个焦点，若，则（ ）‎ A、 B、 C、 D、 ‎ ‎11、平面过正方体ABCD-A1B1C1D1的顶点A,//平面CB1D1,平面ABCD=m,平面AB B1A1=n,则m、n所成角的正弦值为( )‎ A、 B、 C、 D、‎ ‎12、已知函数f(x)＝，若| f(x)|≥ax，则a的取值范围是( )‎ A、（－∞，0] B、（－∞，1] C、[－2，1] D、[－2，0]‎ 二、填空题（每题5分）‎ ‎13、已知两个单位向量，的夹角为，，若，则_____。‎ ‎14．的展开式中的系数为________.（用数字填写答案）‎ ‎15、若满足约束条件，则的最大值为 .‎ ‎16、设等比数列满足a1+a3=10,a2+a4=5,则a1a2 …an的最大值为 ．‎ 三、解答题 ‎17、在△ABC中，内角A，B，C所对的边分别为a，b，c.已知b＋c＝2acosB.‎ ‎(1)证明：A＝2B；‎ ‎(2)若△ABC的面积S＝，求角A的大小．‎ ‎18、某市为了了解本市高中生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将考试成绩进行分组，分组区间为[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，并绘制出频率分布直方图，如图所示．‎ ‎(1)求频率分布直方图中a的值，从该市随机选取一名学生，试估计这名学生参加考试的成绩低于90分的概率；‎ ‎(2)设A，B，C三名学生的考试成绩在区间[80，90)内，M，N两名学生的考试成绩在区间[60，70)内，现从这5名学生中任选两人参加座谈会，求学生M，N至少有一个人被选中的概率；‎ ‎(3)试估计样本的中位数落在哪个分组区间内(只需写出结论)．(注：将频率视为相应的概率)‎ 19、 如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分） ‎ ‎(1)证明：平面PAB⊥平面PAD； ‎ ‎(2)若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值． ‎ ‎20、如图，已知椭圆＋y2＝1，点A，B是它的两个顶点，过原点且斜率为k的直线l与线段AB相交于点D，且与椭圆相交于E，F两点．‎ ‎(1)若＝6，求k的值；‎ ‎(2)求四边形AEBF面积的最大值．‎ ‎21．已知函数f(x)＝ex－x(e为自然对数的底数)．‎ ‎(1)求f(x)的最小值；‎ ‎(2)若对于任意的x∈[0，2]，不等式f(x)>ax恒成立，求实数a的取值范围．‎ ‎22、在平面直角坐标系xOy中，已知曲线C1：(t为参数)与曲线C2：(θ为参数，a>0)．‎ ‎(1)若曲线C1与曲线C2有一个公共点在x轴上，求a的值；‎ ‎(2)当a＝3时，曲线C1与曲线C2交于A，B两点，求A，B两点的距离．‎ ‎2016级高二火箭班3月调研考试 数学（理）试题参考答案 ‎1、‎ ‎2、‎ ‎3、A ‎4、‎ ‎5、‎ ‎6、【答案】B 【解析】由正视图和俯视图知，该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r，圆柱的高为2r，其表面积为==16 + 20，解得r=2，故选B.‎ ‎7、【答案】D 【解析】试题分析：程序在执行过程中，，；；‎ ‎；，程序结束，输出．‎ ‎8、【答案】C【解析】试题分析：用特殊值法,令,,得,选项A错误,,选项B错误,,选项C正确,,选项D错误,故选C．‎ ‎9、‎ ‎10、【答案】B ‎11、【答案】A【解析】试题分析：如图,设平面平面=,平面平面=,因为平面,所以,则所成的角等于所成的角.延长,过作,连接,则为,同理为,而,则所成的角即为所成的角,即为,故所成角的正弦值为,选A.‎ ‎12、‎ ‎13、‎ ‎14、【答案】【解析】试题分析：由题意，展开式通项为，．当时，；当时，，故的展开式中项为，系数为．‎ ‎15、【答案】3【解析】作出可行域如图中阴影部分所示，由斜率的意义知，是可行域内一点与原点连线的斜率，由图可知，点A（1,3）与原点连线的斜率最大，故的最大值为3.‎ ‎16、【答案】【解析】试题分析：设等比数列的公比为,由得,,解得.所以,于是当或时,取得最大值.‎ ‎17、解析　(1)由正弦定理得sinB＋sinC＝2sinAcosB，‎ 故2sinAcosB＝sinB＋sin(A＋B)＝sinB＋sinAcosB＋cosAsinB，于是sinB＝sin(A－B)．‎ 又A，B∈(0，π)，故00)，设D(x0，kx0)，E(x1，kx1)，F(x2，kx2)，其中x10，解得x>0；令f′(x)<0，解得x<0.‎ 从而f(x)在(－∞，0)上单调递减，在(0，＋∞)上单调递增．所以当x＝0时，f(x)取得最小值1.‎ ‎(2)设不等式f(x)>ax的解集为P，则{x|0≤x≤2}⊆P，即对于任意x∈[0，2]，不等式f(x)>ax恒成立．由于f(x)>ax，得(a＋1)x0，解得x>1；令g′(x)<0，解得x<1.从而g(x)在(0，1)上单调递减，在(1，2]上单调递增．所以当x＝1时，g(x)取得最小值e－1，从而实数a的取值范围是(－∞，e－1)．‎ ‎22、解析　(1)曲线C1：的普通方程为y＝3－2x.(1分)‎ 曲线C1与x轴的交点为(，0)．(2分)‎ 曲线C2：的普通方程为＋＝1.(3分)‎ 曲线C2与x轴的交点为(－a，0)，(a，0)．(4分)‎ 由a>0，曲线C1与曲线C2有一个公共点在x轴上，知a＝.(5分)‎ ‎ (2)当a＝3时，曲线C2：为圆x2＋y2＝9.(6分)‎ 圆心到直线y＝3－2x的距离d＝＝.(8分)‎ 所以A，B两点的距离|AB|＝2＝2＝.(10分)‎