- 2021-06-08 发布 |
- 37.5 KB |
- 46页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年高考数学(文科)真题分类汇编G单元 立体几何
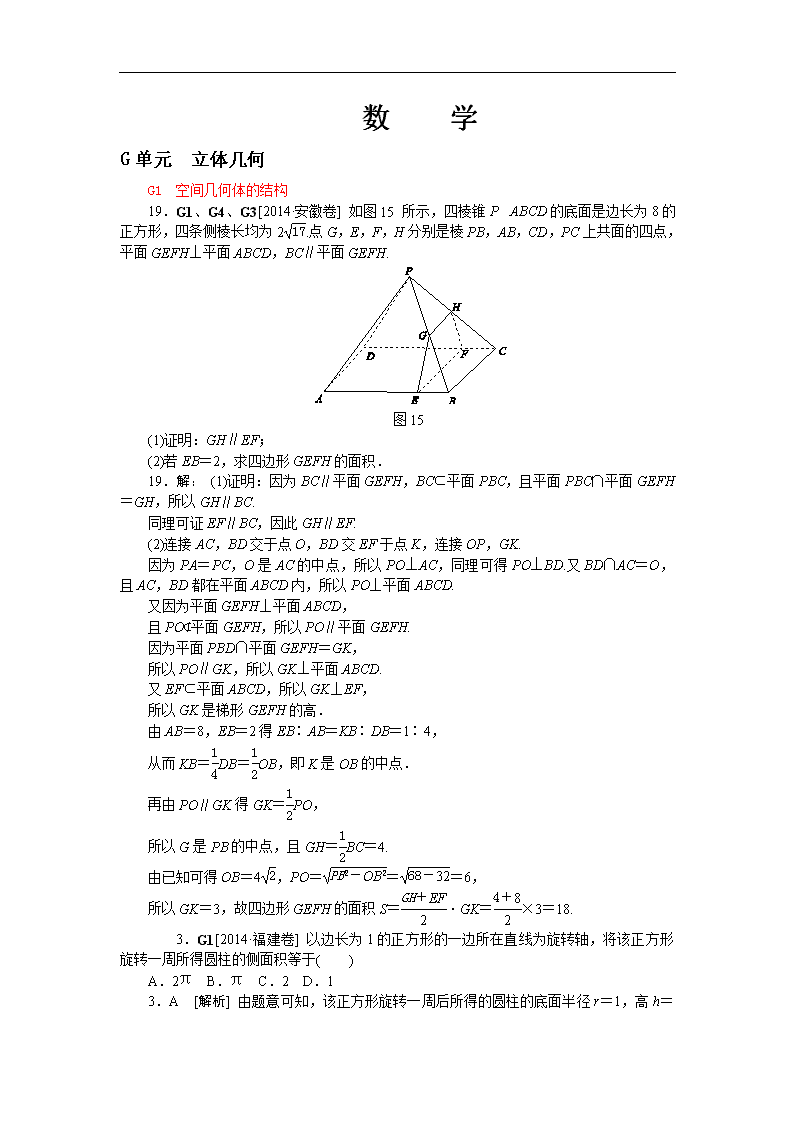
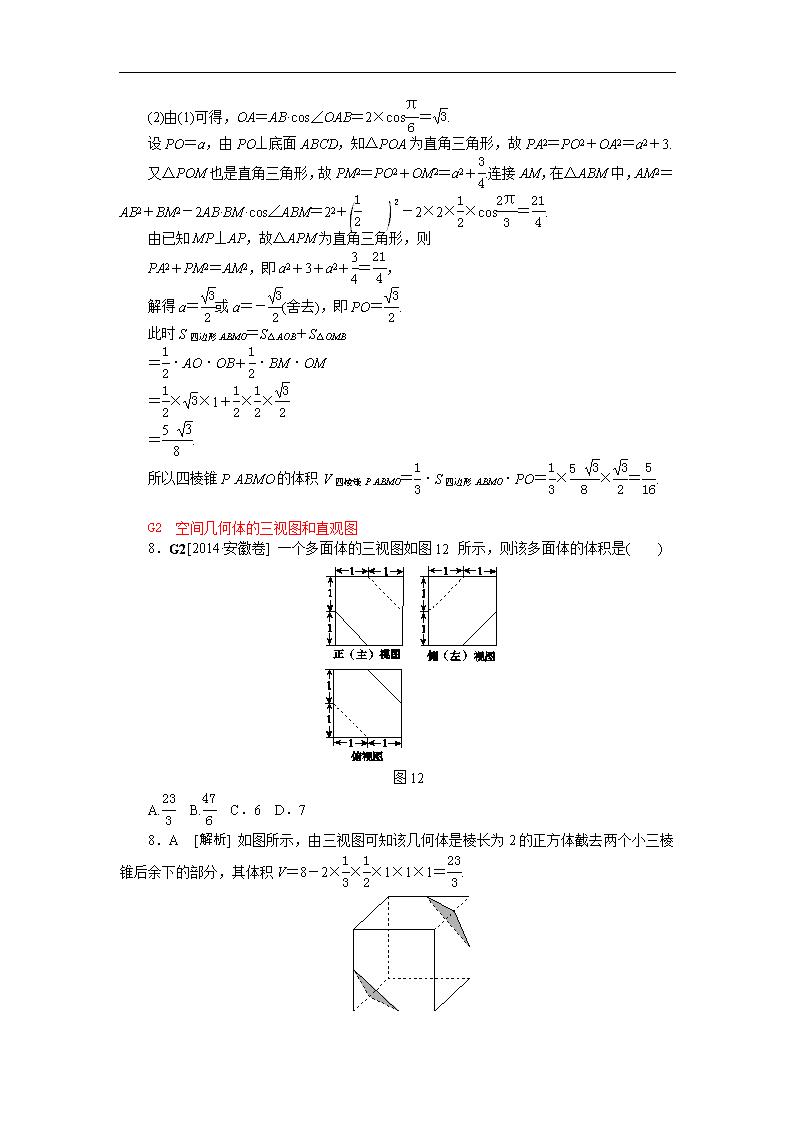
数 学 G 单元 立体几何 G1 空间几何体的结构 19.G1、G4、G3[2014·安徽卷] 如图 15 所示,四棱锥 P ABCD 的底面是边长为 8 的 正方形,四条侧棱长均为 2 17.点 G,E,F,H 分别是棱 PB,AB,CD,PC 上共面的四点, 平面 GEFH⊥平面 ABCD,BC∥平面 GEFH. 图 15 (1)证明:GH∥EF; (2)若 EB=2,求四边形 GEFH 的面积. 19.解: (1)证明:因为 BC∥平面 GEFH,BC⊂平面 PBC,且平面 PBC∩平面 GEFH =GH,所以 GH∥BC. 同理可证 EF∥BC,因此 GH∥EF. (2)连接 AC,BD 交于点 O,BD 交 EF 于点 K,连接 OP,GK. 因为 PA=PC,O 是 AC 的中点,所以 PO⊥AC,同理可得 PO⊥BD.又 BD∩AC=O,且 AC,BD 都在平面 ABCD 内,所以 PO⊥平面 ABCD. 又因为平面 GEFH⊥平面 ABCD, 且 PO⊄平面 GEFH,所以 PO∥平面 GEFH. 因为平面 PBD∩平面 GEFH=GK, 所以 PO∥GK,所以 GK⊥平面 ABCD. 又 EF⊂平面 ABCD,所以 GK⊥EF, 所以 GK 是梯形 GEFH 的高. 由 AB=8,EB=2 得 EB∶AB=KB∶DB=1∶4, 从而 KB=1 4DB=1 2OB,即 K 是 OB 的中点. 再由 PO∥GK 得 GK=1 2PO, 所以 G 是 PB 的中点,且 GH=1 2BC=4. 由已知可得 OB=4 2,PO= PB2-OB2= 68-32=6, 所以 GK=3,故四边形 GEFH 的面积 S=GH+EF 2 ·GK=4+8 2 ×3=18. 3.G1[2014·福建卷] 以边长为 1 的正方形的一边所在直线为旋转轴,将该正方形 旋转一周所得圆柱的侧面积等于( ) A.2π B.π C.2 D.1 3.A [解析] 由题意可知,该正方形旋转一周后所得的圆柱的底面半径 r=1,高 h=1, 则该圆柱的侧面积 S=2πrh=2π,故选 A. 10.G1[2014·湖北卷] 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土, 这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术“置如其周,令相乘 也.又以高乘之,三十六成一.”该术相当于给出了由圆锥的底面周长 L 与高 h,计算其体 积 V 的近似公式 V≈ 1 36L2h.它实际上是将圆锥体积公式中的圆周率π近似取为 3.那么,近似 公式 V≈ 2 75L2h 相当于将圆锥体积公式中的π近似取为( ) A.22 7 B.25 8 C.157 50 D.355 113 10.B [解析] 设圆锥的底面圆半径为 r,底面积为 S,则 L=2πr.由题意得 1 36L2h≈1 3Sh, 代入 S=πr2 化简得π≈3.类比推理,若 V≈ 2 75L2h 时,π≈25 8 .故选 B. 7.G1[2014·新课标全国卷Ⅱ] 正三棱柱 ABC A1B1C1 的底面边长为 2,侧棱长为 3,D 为 BC 中点,则三棱锥 A B1DC1 的体积为( ) A.3 B.3 2 C.1 D. 3 2 7.C [解析] 因为 D 为 BC 的中点,所以 AD⊥BC,故 AD⊥平面 BCC1B1,且 AD= 3, 所以 V 三棱锥 A B1DC1=1 3S△B1DC1×AD=1 3 ×1 2B1C1×BB1×AD=1 3 ×1 2 ×2× 3× 3=1. 20.G1、G5[2014·重庆卷] 如图 14 所示四棱锥 PABCD 中,底面是以 O 为中心的菱 形,PO⊥底面 ABCD,AB=2,∠BAD=π 3 ,M 为 BC 上一点, 且 BM=1 2. (1)证明:BC⊥平面 POM; (2)若 MP⊥AP,求四棱锥 PABMO 的体积. 图 14 20.解:(1)证明:如图所示,因为四边形 ABCD 为菱形,O 为菱形的中心,连接 OB, 则 AO⊥OB.因为∠BAD=π 3 ,所以 OB=AB·sin∠OAB=2sinπ 6 =1. 又因为 BM=1 2 ,且∠OBM=π 3 ,在△OBM 中,OM2=OB2+BM2-2OB·BM·cos∠OBM =12+ 1 2 2 -2×1×1 2 ×cosπ 3 =3 4 ,所以 OB2=OM2+BM2,故 OM⊥BM. 又 PO⊥底面 ABCD,所以 PO⊥BC.从而 BC 与平面 POM 内的两条相交直线 OM,PO 都垂直,所以 BC⊥平面 POM. (2)由(1)可得,OA=AB·cos∠OAB=2×cosπ 6 = 3. 设 PO=a,由 PO⊥底面 ABCD,知△POA 为直角三角形,故 PA2=PO2+OA2=a2+3. 又△POM 也是直角三角形,故 PM2=PO2+OM2=a2+3 4.连接 AM,在△ABM 中,AM2 =AB2+BM2-2AB·BM·cos∠ABM=22+ 1 2 2 -2×2×1 2 ×cos2π 3 =21 4 . 由已知 MP⊥AP,故△APM 为直角三角形,则 PA2+PM2=AM2,即 a2+3+a2+3 4 =21 4 , 解得 a= 3 2 或 a=- 3 2 (舍去),即 PO= 3 2 . 此时 S 四边形 ABMO=S△AOB+S△OMB =1 2 ·AO·OB+1 2 ·BM·OM =1 2 × 3×1+1 2 ×1 2 × 3 2 =5 3 8 . 所以四棱锥 PABMO 的体积 V 四棱锥 PABMO=1 3 ·S 四边形 ABMO·PO=1 3 ×5 3 8 × 3 2 = 5 16. G2 空间几何体的三视图和直观图 8.G2[2014·安徽卷] 一个多面体的三视图如图 12 所示,则该多面体的体积是( ) 图 12 A.23 3 B.47 6 C.6 D.7 8.A [解析] 如图所示,由三视图可知该几何体是棱长为 2 的正方体截去两个小三棱 锥后余下的部分,其体积 V=8-2×1 3 ×1 2 ×1×1×1=23 3 . 11.G2[2014·北京卷] 某三棱锥的三视图如图 13 所示,则该三棱锥最长棱的棱长为 ________. 图 13 11.2 2 [解析] 该三棱锥的直观图如图所示,并且 PB⊥平面 ABC,PB=2,AB=2, AC=BC= 2,PA= 22+22=2 2,PC= 22+( 2)2= 6,故 PA 最长. 7.G2[2014·湖北卷] 在如图 11 所示的空间直角坐标系 O xyz 中,一个四面体的顶点 坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①、②、③、④的四 个图,则该四面体的正视图和俯视图分别为( ) 图 12 A.①和② B.③和① C.④和③ D.④和② 7.D [解析] 由三视图可知,该几何体的正视图显然是一个直角三角形(三个顶点坐标 分别是(0,0,2),(0,2,0),(0,2,2))且内有一虚线(一锐角顶点与一直角边中点的连线), 故正视图是④;俯视图是一个斜三角形,三个顶点坐标分别是(0,0,0),(2,2,0),(1,2, 0),故俯视图是②.故选 D. 8.G2、G8[2014·湖南卷] 一块石材表示的几何体的三视图如图 12 所示,将该石材切 削、打磨,加工成球,则能得到的最大球的半径等于( ) 图 12 A.1 B.2 C.3 D.4 8.B [解析] 由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得 到的最大球为三棱柱的内切球.由题意可知正视图三角形的内切圆的半径即为球的半径,可 得 R=6+8-10 2 =2. 7.G2、G7[2014·辽宁卷] 某几何体三视图如图 12 所示,则该几何体的体积为( ) 图 12 A.8-π 4 B.8-π 2 C.8-π D.8-2π 7.C [解析] 根据三视图可知,该几何体是正方体切去两个体积相等的圆柱的四分之 一后余下的部分,故该几何体体积 V=23-1 2 ×π×12×2=8-π. 3.G2[2014·浙江卷] 某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( ) 图 11 A.72 cm3 B.90 cm3 C.108 cm3 D.138 cm3 3.B [解析] 此几何体是由长方体与三棱柱组合而成的,其体积为 6×4×3+1 2 ×3×4 ×3=90 cm3,故选 B. 6.G2[2014·新课标全国卷Ⅱ] 如图 11,网格纸上正方形小格的边长为 1(表示 1 cm), 图中粗线画出的是某零件的三视图,该零件由一个底面半径为 3 cm,高为 6 cm 的圆柱体毛 坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( ) 图 11 A.17 27 B.5 9 C.10 27 D.1 3 6.C [解析] 该零件是一个由两个圆柱组成的组合体,其体积 V=π×32×2+π×22 ×4=34π(cm3),原毛坯的体积 V 毛坯=π×32×6=54π(cm3),被切部分的体积 V 切=V 毛坯 -V=54π-34π=20π(cm3),所以 V 切 V 毛坯 =20π 54π =10 27. 8.G2[2014·全国新课标卷Ⅰ] 如图 11,网格纸的各小格都是正方形,粗实线画出的是 一个几何体的三视图,则这个几何体是( ) A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 8.B [解析] 从俯视图为矩形可以看出,此几何体不可能是三棱锥或四棱锥,其直观 图如图,是一个三棱柱. 17.G2、G8[2014·陕西卷] 四面体 ABCD 及其三视图如图 14 所示,平行于棱 AD,BC 的平面分别交四面体的棱 AB,BD,DC,CA 于点 E,F,G,H. 图 14 (1)求四面体 ABCD 的体积; (2)证明:四边形 EFGH 是矩形. 17.解:(1)由该四面体的三视图可知, BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1, ∴AD⊥平面 BDC, ∴四面体 ABCD 的体积 V=1 3 ×1 2 ×2×2×1=2 3. (2)证明:∵BC∥平面 EFGH,平面 EFGH∩平面 BDC=FG,平面 EFGH∩ 平面 ABC =EH, ∴BC∥FG,BC∥EH,∴FG∥EH. 同理 EF∥AD,HG∥AD,∴EF∥HG, ∴四边形 EFGH 是平行四边形. 又∵AD⊥平面 BDC,∴AD⊥BC,∴EF⊥FG, ∴四边形 EFGH 是矩形. 4.G2[2014·四川卷] 某三棱锥的侧视图、俯视图如图 11 所示,则该三棱锥的体积是(锥 体体积公式:V=1 3Sh,其中 S 为底面面积,h 为高)( ) 图 11 A.3 B.2 C. 3 D.1 4.D [解析] 由图可知,三棱锥的底面为边长为 2 的正三角形,左侧面垂直于底面, 且为边长为 2 的正三角形,所以该三棱锥的底面积 S=1 2 ×2× 3,高 h= 3,所以其体积 V =1 3Sh=1 3 × 3× 3=1,故选 D. 7.G2[2014·重庆卷] 某几何体的三视图如图 12 所示,则该几何体的体积为( ) 图 12 A.12 B.18 C.24 D.30 7.C [解析] 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥得到的.三棱 柱的底面是一个两直角边长分别为 3 和 4 的直角三角形,高为 5;截去的锥体的底面是两直 角边的长分别为 3 和 4 的直角三角形,高为 3,所以该几何体的体积为 V=1 2 ×3×4×5-1 3 × 1 2 ×3×4×3=24. 10.G2[2014·天津卷] 一个几何体的三视图如图 12 所示(单位:m),则该几何体的体积 为________m3. 10.20π 3 [解析] 由三视图可知,该几何体为圆柱与圆锥的组合体,其体积 V=π×12 ×4+1 3 π×22×2=20π 3 . G3 平面的基本性质、空间两条直线 19.G1、G4、G3[2014·安徽卷] 如图 15 所示,四棱锥 P ABCD 的底面是边长为 8 的 正方形,四条侧棱长均为 2 17.点 G,E,F,H 分别是棱 PB,AB,CD,PC 上共面的四点, 平面 GEFH⊥平面 ABCD,BC∥平面 GEFH. 图 15 (1)证明:GH∥EF; (2)若 EB=2,求四边形 GEFH 的面积. 19.解: (1)证明:因为 BC∥平面 GEFH,BC⊂平面 PBC,且平面 PBC∩平面 GEFH =GH,所以 GH∥BC. 同理可证 EF∥BC,因此 GH∥EF. (2)连接 AC,BD 交于点 O,BD 交 EF 于点 K,连接 OP,GK. 因为 PA=PC,O 是 AC 的中点,所以 PO⊥AC,同理可得 PO⊥BD.又 BD∩AC=O,且 AC,BD 都在平面 ABCD 内,所以 PO⊥平面 ABCD. 又因为平面 GEFH⊥平面 ABCD, 且 PO⊄平面 GEFH,所以 PO∥平面 GEFH. 因为平面 PBD∩平面 GEFH=GK, 所以 PO∥GK,所以 GK⊥平面 ABCD. 又 EF⊂平面 ABCD,所以 GK⊥EF, 所以 GK 是梯形 GEFH 的高. 由 AB=8,EB=2 得 EB∶AB=KB∶DB=1∶4, 从而 KB=1 4DB=1 2OB,即 K 是 OB 的中点. 再由 PO∥GK 得 GK=1 2PO, 所以 G 是 PB 的中点,且 GH=1 2BC=4. 由已知可得 OB=4 2,PO= PB2-OB2= 68-32=6, 所以 GK=3,故四边形 GEFH 的面积 S=GH+EF 2 ·GK=4+8 2 ×3=18. 18.G5、G3[2014·湖南卷] 如图 13 所示,已知二面角αMNβ的大小为 60°,菱形 ABCD 在面β内,A,B 两点在棱 MN 上,∠BAD=60°,E 是 AB 的中点,DO⊥面α,垂足为 O. 图 13 (1)证明:AB⊥平面 ODE; (2)求异面直线 BC 与 OD 所成角的余弦值. 18.解:(1)证明:如图,因为 DO⊥α,AB⊂α,所以 DO⊥AB. 连接 BD,由题设知,△ABD 是正三角形,又 E 是 AB 的中点,所以 DE⊥AB.而 DO∩DE =D,故 AB⊥平面 ODE. (2)因为 BC∥AD,所以 BC 与 OD 所成的角等于 AD 与 OD 所成的角,即∠ADO 是 BC 与 OD 所成的角. 由(1)知,AB⊥平面 ODE,所以 AB⊥OE.又 DE⊥AB,于是∠DEO 是二面角αMNβ的平 面角,从而∠DEO=60°. 不妨设 AB=2,则 AD=2,易知 DE= 3. 在 Rt△DOE 中,DO=DE·sin 60°=3 2. 连接 AO,在 Rt△AOD 中,cos∠ADO=DO AD = 3 2 2 =3 4. 故异面直线 BC 与 OD 所成角的余弦值为3 4. 4.G3[2014·辽宁卷] 已知 m,n 表示两条不同直线,α表示平面.下列说法正确的是 ( ) A.若 m∥α,n∥α,则 m∥n B.若 m⊥α,n⊂α,则 m⊥n C.若 m⊥α,m⊥n,则 n∥α D.若 m∥α,m⊥n,则 n⊥α 4.B [解析] 由题可知,若 m∥α,n∥α,则 m 与 n 平行、相交或异面,所以 A 错误; 若 m⊥α,n⊂α,则 m⊥n,故 B 正确;若 m⊥α,m⊥n,则 n∥α或 n⊂α,故 C 错误;若 m∥α,m⊥n,则 n∥α或 n⊥α或 n 与α相交,故 D 错误. G4 空间中的平行关系 6.G4、G5[2014·浙江卷] 设 m,n 是两条不同的直线,α,β是两个不同的平面( ) A.若 m⊥n,n∥α,则 m⊥α B.若 m∥β,β⊥α,则 m⊥α C.若 m⊥β,n⊥β,n⊥α,则 m⊥α D.若 m⊥n,n⊥β,β⊥α,则 m⊥α 6.C [解析] A,B,D 中 m 与平面α可能平行、相交或 m 在平面内α;对于 C,若 m⊥β, n⊥β,则 m∥n,而 n⊥α,所以 m⊥α.故选 C. 19.G1、G4、G3[2014·安徽卷] 如图 15 所示,四棱锥 P ABCD 的底面是边长为 8 的 正方形,四条侧棱长均为 2 17.点 G,E,F,H 分别是棱 PB,AB,CD,PC 上共面的四点, 平面 GEFH⊥平面 ABCD,BC∥平面 GEFH. 图 15 (1)证明:GH∥EF; (2)若 EB=2,求四边形 GEFH 的面积. 19.解: (1)证明:因为 BC∥平面 GEFH,BC⊂平面 PBC,且平面 PBC∩平面 GEFH =GH,所以 GH∥BC. 同理可证 EF∥BC,因此 GH∥EF. (2)连接 AC,BD 交于点 O,BD 交 EF 于点 K,连接 OP,GK. 因为 PA=PC,O 是 AC 的中点,所以 PO⊥AC,同理可得 PO⊥BD.又 BD∩AC=O,且 AC,BD 都在平面 ABCD 内,所以 PO⊥平面 ABCD. 又因为平面 GEFH⊥平面 ABCD, 且 PO⊄平面 GEFH,所以 PO∥平面 GEFH. 因为平面 PBD∩平面 GEFH=GK, 所以 PO∥GK,所以 GK⊥平面 ABCD. 又 EF⊂平面 ABCD,所以 GK⊥EF, 所以 GK 是梯形 GEFH 的高. 由 AB=8,EB=2 得 EB∶AB=KB∶DB=1∶4, 从而 KB=1 4DB=1 2OB,即 K 是 OB 的中点. 再由 PO∥GK 得 GK=1 2PO, 所以 G 是 PB 的中点,且 GH=1 2BC=4. 由已知可得 OB=4 2,PO= PB2-OB2= 68-32=6, 所以 GK=3,故四边形 GEFH 的面积 S=GH+EF 2 ·GK=4+8 2 ×3=18. 17.G4 、G5[2014·北京卷] 如图 15,在三棱柱 ABC A1B1C1 中,侧棱垂直于底面, AB⊥BC,AA1=AC=2,BC=1,E,F 分别是 A1C1,BC 的中点. 图 15 (1)求证:平面 ABE⊥平面 B1BCC1; (2)求证:C1F∥平面 ABE; (3)求三棱锥 E ABC 的体积. 17.解:(1)证明:在三棱柱 ABC A1B1C1 中,BB1⊥底面 ABC, 所以 BB1⊥AB. 又因为 AB⊥BC, 所以 AB⊥平面 B1BCC1. 所以平面 ABE⊥平面 B1BCC1. (2)证明:取 AB 的中点 G,连接 EG,FG. 因为 E,F,G 分别是 A1C1,BC,AB 的中点, 所以 FG∥AC,且 FG=1 2AC,EC1=1 2A1C1. 因为 AC∥A1C1,且 AC=A1C1, 所以 FG∥EC1,且 FG=EC1, 所以四边形 FGEC1 为平行四边形, 所以 C1F∥EG. 又因为 EG⊂平面 ABE,C1F⊄平面 ABE, 所以 C1F∥平面 ABE. (3)因为 AA1=AC=2,BC=1,AB⊥BC, 所以 AB= AC2-BC2= 3. 所以三棱锥 E ABC 的体积 V=1 3S△ABC·AA1=1 3 ×1 2 × 3×1×2= 3 3 . 20.G4、G5[2014·湖北卷] 如图 15,在正方体 ABCD A1B1C1D1 中,E,F,P,Q,M, N 分别是棱 AB,AD,DD1,BB1,A1B1,A1D1 的中点.求证: (1)直线 BC1∥平面 EFPQ; (2)直线 AC1⊥平面 PQMN. 图 15 20.证明:(1)连接 AD1,由 ABCD A1B1C1D1 是正方体, 知 AD1∥BC1. 因为 F,P 分别是 AD,DD1 的中点,所以 FP∥AD1. 从而 BC1∥FP. 而 FP⊂平面 EFPQ,且 BC1⊄平面 EFPQ, 故直线 BC1∥平面 EFPQ. (2)如图,连接 AC,BD,A1C1,则 AC⊥BD. 由 CC1⊥平面 ABCD,BD⊂平面 ABCD, 可得 CC1⊥BD. 又 AC∩CC1=C,所以 BD⊥平面 ACC1A1. 而 AC1⊂平面 ACC1A1,所以 BD⊥AC1. 因为 M,N 分别是 A1B1,A1D1 的中点,所以 MN∥BD,从而 MN⊥AC1. 同理可证 PN⊥AC1. 又 PN∩MN=N,所以直线 AC1⊥平面 PQMN. 16.G4、G5[2014·江苏卷] 如图 14 所示,在三棱锥 P ABC 中,D,E,F 分别为棱 PC,AC,AB 的中点.已知 PA⊥AC,PA=6,BC=8,DF=5. 求证:(1)直线 PA∥平面 DEF; (2)平面 BDE⊥平面 ABC. 图 14 16.证明: (1)因为 D,E 分别为棱 PC,AC 的中点,所以 DE∥PA.又因为 PA⊄平面 DEF, DE⊂平面 DEF,所以直线 PA∥平面 DEF. (2)因为 D,E,F 分别为棱 PC,AC,AB 的中点,PA=6,BC=8,所以 DE∥PA,DE =1 2PA=3,EF=1 2BC=4.又因为 DF=5,所以 DF2=DE2+EF2,所以∠DEF=90°,即 DE⊥EF. 又 PA⊥AC,DE∥PA,所以 DE⊥AC.因为 AC∩EF=E,AC⊂平面 ABC,EF⊂平面 ABC, 所以 DE⊥平面 ABC. 又 DE⊂平面 BDE,所以平面 BDE⊥平面 ABC. 18.G4、G11[2014·新课标全国卷Ⅱ] 如图 13,四棱锥 P ABCD 中,底面 ABCD 为矩 形,PA⊥平面 ABCD,E 为 PD 的中点. (1)证明:PB∥平面 AEC; (2)设 AP=1,AD= 3,三棱锥 P ABD 的体积 V= 3 4 ,求 A 到平面 PBC 的距离. 图 13 18.解:(1)证明:设 BD 与 AC 的交点为 O,连接 EO. 因为 ABCD 为矩形,所以 O 为 BD 的中点. 又 E 为 PD 的中点,所以 EO∥PB. EO⊂平面 AEC,PB⊄平面 AEC, 所以 PB∥平面 AEC. (2)V=1 3 ×1 2 ×PA×AB×AD= 3 6 AB, 由 V= 3 4 ,可得 AB=3 2. 作 AH⊥PB 交 PB 于点 H. 由题设知 BC⊥平面 PAB,所以 BC⊥AH, 因为 PB∩BC=B,所以 AH⊥平面 PBC. 又 AH=PA·AB PB =3 13 13 , 所以点 A 到平面 PBC 的距离为3 13 13 . 18.G5,G4[2014·山东卷] 如图 14 所示,四棱锥 PABCD 中,AP⊥平面 PCD,AD∥BC, AB=BC=1 2AD,E,F 分别为线段 AD,PC 的中点. 图 14 (1)求证:AP∥平面 BEF; (2)求证:BE⊥平面 PAC. 18.证明:(1)设 AC∩BE=O,连接 OF,EC.由于 E 为 AD 的中点, AB=BC=1 2AD,AD∥BC, 所以 AE∥BC,AE=AB=BC, 所以 O 为 AC 的中点. 又在△PAC 中,F 为 PC 的中点,所以 AP∥OF. 又 OF⊂平面 BEF,AP⊄平面 BEF, 所以 AP∥平面 BEF. (2)由题意知,ED∥BC,ED=BC, 所以四边形 BCDE 为平行四边形, 所以 BE∥CD. 又 AP⊥平面 PCD, 所以 AP⊥CD,所以 AP⊥BE. 因为四边形 ABCE 为菱形, 所以 BE⊥AC. 又 AP∩AC=A,AP,AC⊂平面 PAC, 所以 BE⊥平面 PAC. 18.G4、G5[2014·四川卷] 在如图 14 所示的多面体中,四边形 ABB1A1 和 ACC1A1 都为 矩形. (1)若 AC⊥BC,证明:直线 BC⊥平面 ACC1A1. (2)设 D,E 分别是线段 BC,CC1 的中点,在线段 AB 上是否存在一点 M,使直线 DE∥ 平面 A1MC?请证明你的结论. 图 14 18.解:(1)证明:因为四边形 ABB1A1 和 ACC1A1 都是矩形, 所以 AA1⊥AB,AA1⊥AC. 因为 AB,AC 为平面 ABC 内的两条相交直线, 所以 AA1⊥平面 ABC. 因为直线 BC⊂平面 ABC,所以 AA1⊥BC. 又由已知,AC⊥BC,AA1,AC 为平面 ACC1A1 内的两条相交直线, 所以 BC⊥平面 ACC1A1. (2)取线段 AB 的中点 M,连接 A1M,MC,A1C,AC1,设 O 为 A1C,AC1 的交点. 图 14 由已知,O 为 AC1 的中点. 连接 MD,OE,则 MD,OE 分别为△ABC,△ACC1 的中位线, 所以 MD 綊 1 2AC,OE 綊 1 2AC, 因此 MD 綊 OE. 连接 OM,从而四边形 MDEO 为平行四边形,所以 DE∥MO. 因为直线 DE⊄平面 A1MC,MO⊂平面 A1MC. 所以直线 DE∥平面 A1MC. 即线段 AB 上存在一点 M(线段 AB 的中点),使直线 DE∥平面 A1MC. 17.G4、G5、G11[2014·天津卷] 如图 14 所示,四棱锥 P ABCD 的底面 ABCD 是平 行四边形,BA=BD= 2,AD=2,PA=PD= 5,E,F 分别是棱 AD,PC 的中点. (1)证明:EF∥平面 PAB; (2)若二面角 PADB 为 60°. (i)证明:平面 PBC⊥平面 ABCD; (ii)求直线 EF 与平面 PBC 所成角的正弦值. 17.解:(1)证明:如图所示,取 PB 中点 M,连接 MF,AM.因为 F 为 PC 中点,所以 MF∥BC,且 MF=1 2BC.由已知有 BC∥AD,BC=AD,又由于 E 为 AD 中点,因而 MF∥AE 且 MF=AE,故四边形 AMFE 为平行四边形,所以 EF∥AM.又 AM⊂平面 PAB,而 EF⊄平面 PAB,所以 EF∥平面 PAB. (2)(i)证明:连接 PE,BE.因为 PA=PD,BA=BD,而 E 为 AD 中点,所以 PE⊥AD, BE⊥AD,所以∠PEB 为二面角 P AD B 的平面角.在△PAD 中,由 PA=PD= 5,AD=2, 可解得 PE=2.在△ABD 中,由 BA=BD= 2,AD=2,可解得 BE=1.在△PEB 中,PE=2, BE=1,∠PEB=60˚,由余弦定理,可解得 PB= 3,从而∠PBE=90˚,即 BE⊥PB.又 BC∥AD, BE⊥AD,从而 BE⊥BC,因此 BE⊥平面PBC.又BE⊂平面 ABCD,所以平面PBC⊥平面ABCD. (ii)连接 BF,由(i)知,BE⊥平面 PBC,所以∠EFB 为直线 EF 与平面 PBC 所成的角.由 PB= 3及已知,得∠ABP 为直角,而 MB=1 2PB= 3 2 ,可得 AM= 11 2 ,故 EF= 11 2 .又 BE =1,故在直角三角形 EBF 中,sin∠EFB=BE EF =2 11 11 .所以直线 EF 与平面 PBC 所成角的正 弦值为2 11 11 . G5 空间中的垂直关系 6.G4、G5[2014·浙江卷] 设 m,n 是两条不同的直线,α,β是两个不同的平面( ) A.若 m⊥n,n∥α,则 m⊥α B.若 m∥β,β⊥α,则 m⊥α C.若 m⊥β,n⊥β,n⊥α,则 m⊥α D.若 m⊥n,n⊥β,β⊥α,则 m⊥α 6.C [解析] A,B,D 中 m 与平面α可能平行、相交或 m 在平面内α;对于 C,若 m⊥β, n⊥β,则 m∥n,而 n⊥α,所以 m⊥α.故选 C. 17.G4 、G5[2014·北京卷] 如图 15,在三棱柱 ABC A1B1C1 中,侧棱垂直于底面, AB⊥BC,AA1=AC=2,BC=1,E,F 分别是 A1C1,BC 的中点. 图 15 (1)求证:平面 ABE⊥平面 B1BCC1; (2)求证:C1F∥平面 ABE; (3)求三棱锥 E ABC 的体积. 17.解:(1)证明:在三棱柱 ABC A1B1C1 中,BB1⊥底面 ABC, 所以 BB1⊥AB. 又因为 AB⊥BC, 所以 AB⊥平面 B1BCC1. 所以平面 ABE⊥平面 B1BCC1. (2)证明:取 AB 的中点 G,连接 EG,FG. 因为 E,F,G 分别是 A1C1,BC,AB 的中点, 所以 FG∥AC,且 FG=1 2AC,EC1=1 2A1C1. 因为 AC∥A1C1,且 AC=A1C1, 所以 FG∥EC1,且 FG=EC1, 所以四边形 FGEC1 为平行四边形, 所以 C1F∥EG. 又因为 EG⊂平面 ABE,C1F⊄平面 ABE, 所以 C1F∥平面 ABE. (3)因为 AA1=AC=2,BC=1,AB⊥BC, 所以 AB= AC2-BC2= 3. 所以三棱锥 E ABC 的体积 V=1 3S△ABC·AA1=1 3 ×1 2 × 3×1×2= 3 3 . 19.G5,G7[2014·福建卷] 如图 16 所示,三棱锥 A BCD 中,AB⊥平面 BCD,CD ⊥BD. (1)求证:CD⊥平面 ABD; (2)若 AB=BD=CD=1,M 为 AD 中点,求三棱锥 A MBC 的体积. 图 16 19.解:方法一:(1)证明:∵AB⊥平面 BCD,CD⊂平面 BCD, ∴AB⊥CD. 又∵CD⊥BD,AB∩BD=B, AB⊂平面 ABD,BD⊂平面 ABD, ∴CD⊥平面 ABD. (2)由 AB⊥平面 BCD, 得 AB⊥BD. ∵AB=BD=1,∴S△ABD=1 2. ∵M 是 AD 的中点, ∴S△ABM=1 2S△ABD=1 4. 由(1)知,CD⊥平面 ABD, ∴三棱锥 C ABM 的高 h=CD=1, 因此三棱锥 A MBC 的体积 VA MBC=VC ABM=1 3S△ABM·h= 1 12. 方法二:(1)同方法一. (2)由 AB⊥平面 BCD,得平面 ABD⊥平面 BCD. 且平面 ABD∩平面 BCD=BD. 如图所示,过点 M 作 MN⊥BD 交 BD 于点 N, 则 MN⊥平面 BCD,且 MN=1 2AB=1 2. 又 CD⊥BD,BD=CD=1,∴S△BCD=1 2. ∴三棱锥 A MBC 的体积 VA MBC=VA BCD-VM BCD =1 3AB·S△BCD-1 3MN·S△BCD = 1 12. 18.G5、G7[2014·广东卷] 如图 12 所示,四边形 ABCD 为矩形,PD⊥平面 ABCD, AB=1,BC=PC=2,作如图 13 折叠:折痕 EF∥DC,其中点 E,F 分别在线段 PD,PC 上,沿 EF 折叠后点 P 叠在线段 AD 上的点记为 M,并且 MF⊥CF. (1)证明:CF⊥平面 MDF; (2)求三棱锥 M CDE 的体积. 图 12 图 13 20.G4、G5[2014·湖北卷] 如图 15,在正方体 ABCD A1B1C1D1 中,E,F,P,Q,M, N 分别是棱 AB,AD,DD1,BB1,A1B1,A1D1 的中点.求证: (1)直线 BC1∥平面 EFPQ; (2)直线 AC1⊥平面 PQMN. 图 15 20.证明:(1)连接 AD1,由 ABCD A1B1C1D1 是正方体, 知 AD1∥BC1. 因为 F,P 分别是 AD,DD1 的中点,所以 FP∥AD1. 从而 BC1∥FP. 而 FP⊂平面 EFPQ,且 BC1⊄平面 EFPQ, 故直线 BC1∥平面 EFPQ. (2)如图,连接 AC,BD,A1C1,则 AC⊥BD. 由 CC1⊥平面 ABCD,BD⊂平面 ABCD, 可得 CC1⊥BD. 又 AC∩CC1=C,所以 BD⊥平面 ACC1A1. 而 AC1⊂平面 ACC1A1,所以 BD⊥AC1. 因为 M,N 分别是 A1B1,A1D1 的中点,所以 MN∥BD,从而 MN⊥AC1. 同理可证 PN⊥AC1. 又 PN∩MN=N,所以直线 AC1⊥平面 PQMN. 18.G5、G3[2014·湖南卷] 如图 13 所示,已知二面角αMNβ的大小为 60°,菱形 ABCD 在面β内,A,B 两点在棱 MN 上,∠BAD=60°,E 是 AB 的中点,DO⊥面α,垂足为 O. 图 13 (1)证明:AB⊥平面 ODE; (2)求异面直线 BC 与 OD 所成角的余弦值. 18.解:(1)证明:如图,因为 DO⊥α,AB⊂α,所以 DO⊥AB. 连接 BD,由题设知,△ABD 是正三角形,又 E 是 AB 的中点,所以 DE⊥AB.而 DO∩DE =D,故 AB⊥平面 ODE. (2)因为 BC∥AD,所以 BC 与 OD 所成的角等于 AD 与 OD 所成的角,即∠ADO 是 BC 与 OD 所成的角. 由(1)知,AB⊥平面 ODE,所以 AB⊥OE.又 DE⊥AB,于是∠DEO 是二面角αMNβ的平 面角,从而∠DEO=60°. 不妨设 AB=2,则 AD=2,易知 DE= 3. 在 Rt△DOE 中,DO=DE·sin 60°=3 2. 连接 AO,在 Rt△AOD 中,cos∠ADO=DO AD = 3 2 2 =3 4. 故异面直线 BC 与 OD 所成角的余弦值为3 4. 16.G4、G5[2014·江苏卷] 如图 14 所示,在三棱锥 P ABC 中,D,E,F 分别为棱 PC,AC,AB 的中点.已知 PA⊥AC,PA=6,BC=8,DF=5. 求证:(1)直线 PA∥平面 DEF; (2)平面 BDE⊥平面 ABC. 18.G5,G4[2014·山东卷] 如图 14 所示,四棱锥 PABCD 中,AP⊥平面 PCD,AD∥BC, AB=BC=1 2AD,E,F 分别为线段 AD,PC 的中点. 图 14 (1)求证:AP∥平面 BEF; (2)求证:BE⊥平面 PAC. 18.证明:(1)设 AC∩BE=O,连接 OF,EC.由于 E 为 AD 的中点, AB=BC=1 2AD,AD∥BC, 所以 AE∥BC,AE=AB=BC, 所以 O 为 AC 的中点. 又在△PAC 中,F 为 PC 的中点,所以 AP∥OF. 又 OF⊂平面 BEF,AP⊄平面 BEF, 所以 AP∥平面 BEF. (2)由题意知,ED∥BC,ED=BC, 所以四边形 BCDE 为平行四边形, 所以 BE∥CD. 又 AP⊥平面 PCD, 所以 AP⊥CD,所以 AP⊥BE. 因为四边形 ABCE 为菱形, 所以 BE⊥AC. 又 AP∩AC=A,AP,AC⊂平面 PAC, 所以 BE⊥平面 PAC. 图 14 16.证明: (1)因为 D,E 分别为棱 PC,AC 的中点,所以 DE∥PA.又因为 PA⊄平面 DEF, DE⊂平面 DEF,所以直线 PA∥平面 DEF. (2)因为 D,E,F 分别为棱 PC,AC,AB 的中点,PA=6,BC=8,所以 DE∥PA,DE =1 2PA=3,EF=1 2BC=4.又因为 DF=5,所以 DF2=DE2+EF2,所以∠DEF=90°,即 DE⊥EF. 又 PA⊥AC,DE∥PA,所以 DE⊥AC.因为 AC∩EF=E,AC⊂平面 ABC,EF⊂平面 ABC, 所以 DE⊥平面 ABC. 又 DE⊂平面 BDE,所以平面 BDE⊥平面 ABC. 19.G5、G7[2014·江西卷] 如图 11 所示,三棱柱 ABC A1B1C1 中,AA1⊥BC,A1B⊥ BB1. (1)求证:A1C⊥CC1; (2)若 AB=2,AC= 3,BC= 7,问 AA1 为何值时,三棱柱 ABC A1B1C1 体积最大,并 求此最大值. 图 11 19.解:(1)证明:由 AA1⊥BC 知 BB1⊥BC.又 BB1⊥A1B,故 BB1⊥平面 BCA1,所以 BB1 ⊥A1C. 又 BB1∥CC1,所以 A1C⊥CC1. (2)方法一:设 AA1=x. 在 Rt△A1BB1 中,A1B= A1B21-BB21= 4-x2. 同理,A1C= A1C21-CC21= 3-x2. 在△A1BC 中, cos∠BA1C=A1B2+A1C2-BC2 2A1B·A1C = - x2 (4-x2)(3-x2) , sin∠BA1C= 12-7x2 (4-x2)(3-x2) , 所以 S△A1BC=1 2A1B·A1C·sin∠BA1C= 12-7x2 2 . 从而三棱柱 ABC A1B1C1 的体积 V=S 直·l=S△A1BC·AA1=x 12-7x2 2 . 因为 x 12-7x2= 12x2-7x4= -7 x2-6 7 2 +36 7 , 所以当 x= 6 7 = 42 7 ,即 AA1= 42 7 时,体积 V 取到最大值3 7 7 . (2)方法二:过 A1 作 BC 的垂线,垂足为 D,连接 AD. 由 AA1⊥BC,A1D⊥BC,得 BC⊥平面 AA1D,故 BC⊥AD.又∠BAC=90°, 所以 S△ABC=1 2AD·BC=1 2AB·AC,得 AD=2 21 7 . 设 AA1=x.在 Rt△AA1D 中, A1D= AD2-AA21= 12 7 -x2, S△A1BC=1 2A1D·BC= 12-7x2 2 . 从而三棱柱 ABC A1B1C1 的体积 V=S 直·l=S△A1BC·AA1=x 12-7x2 2 .因为 x 12-7x2 = 12x2-7x4= -7 x2-6 7 2 +36 7 , 所以当 x= 6 7 = 42 7 ,即 AA1= 42 7 时,体积 V 取到最大值3 7 7 . 19.G5、G7[2014·辽宁卷] 如图 14 所示,△ABC 和△BCD 所在平面互相垂直,且 AB =BC=BD=2,∠ABC=∠DBC=120°,E,F,G 分别为 AC,DC,AD 的中点. 图 14 (1)求证:EF⊥平面 BCG; (2)求三棱锥 D BCG 的体积. 附:锥体的体积公式 V=1 3Sh,其中 S 为底面面积,h 为高. 19.解:(1)证明:由已知得△ABC≌△DBC, 因此 AC=DC. 又 G 为 AD 的中点,所以 CG⊥AD, 同理 BG⊥AD.又 BG∩CG=G,所以 AD⊥平面 BGC. 又 EF∥AD,所以 EF⊥平面 BCG. (2)在平面 ABC 内,作 AO⊥CB,交 CB 延长线于点 O. 由平面 ABC⊥平面 BCD,知 AO⊥平面 BDC. 又 G 为 AD 的中点,所以 G 到平面 BDC 的距离 h 是 AO 长度的一半. 在△AOB 中,AO=AB·sin 60°= 3,所以 V 三棱锥 D BCG=V 三棱锥 G BCD=1 3 ·S△DBC·h=1 3 ×1 2 ·BD·BC·sin 120°· 3 2 =1 2. 19.G5 G11[2014·全国新课标卷Ⅰ] 如图 14,三棱柱 ABC A1B1C1 中,侧面 BB1C1C 为菱形,B1C 的中点为 O,且 AO⊥平面 BB1C1C. 图 14 (1)证明:B1C⊥AB; (2)若 AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱 ABC A1B1C1 的高. 19.解:(1)证明:连接 BC1,则 O 为 B1C 与 BC1 的交点. 因为侧面 BB1C1C 为菱形,所以 B1C⊥BC1. 又 AO⊥平面 BB1C1C,所以 B1C⊥AO, 由于 BC1∩AO=O,故 B1C⊥平面 ABO. 由于 AB⊂平面 ABO,故 B1C⊥AB. (2)作 OD⊥BC,垂足为 D,连接 AD.作 OH⊥AD,垂足为 H. 由于 BC⊥AO,BC⊥OD,且 AO∩OD=O, 故 BC⊥平面 AOD,所以 OH⊥BC. 又 OH⊥AD,且 AD∩BC=D, 所以 OH⊥平面 ABC. 因为∠CBB1=60°,所以△CBB1 为等边三角形,又 BC=1,可得 OD= 3 4 . 因为 AC⊥AB1,所以 OA=1 2B1C=1 2. 由 OH·AD=OD·OA,且 AD= OD2+OA2= 7 4 ,得 OH= 21 14 . 又 O 为 B1C 的中点,所以点 B1 到平面 ABC 的距离为 21 7 .故三棱柱 ABC A1B1C1 的高为 21 7 . 18.G4、G5[2014·四川卷] 在如图 14 所示的多面体中,四边形 ABB1A1 和 ACC1A1 都为 矩形. (1)若 AC⊥BC,证明:直线 BC⊥平面 ACC1A1. (2)设 D,E 分别是线段 BC,CC1 的中点,在线段 AB 上是否存在一点 M,使直线 DE∥ 平面 A1MC?请证明你的结论. 图 14 18.解:(1)证明:因为四边形 ABB1A1 和 ACC1A1 都是矩形, 所以 AA1⊥AB,AA1⊥AC. 因为 AB,AC 为平面 ABC 内的两条相交直线, 所以 AA1⊥平面 ABC. 因为直线 BC⊂平面 ABC,所以 AA1⊥BC. 又由已知,AC⊥BC,AA1,AC 为平面 ACC1A1 内的两条相交直线, 所以 BC⊥平面 ACC1A1. (2)取线段 AB 的中点 M,连接 A1M,MC,A1C,AC1,设 O 为 A1C,AC1 的交点. 图 14 由已知,O 为 AC1 的中点. 连接 MD,OE,则 MD,OE 分别为△ABC,△ACC1 的中位线, 所以 MD 綊 1 2AC,OE 綊 1 2AC, 因此 MD 綊 OE. 连接 OM,从而四边形 MDEO 为平行四边形,所以 DE∥MO. 因为直线 DE⊄平面 A1MC,MO⊂平面 A1MC. 所以直线 DE∥平面 A1MC. 即线段 AB 上存在一点 M(线段 AB 的中点),使直线 DE∥平面 A1MC. 17.G4、G5、G11[2014·天津卷] 如图 14 所示,四棱锥 P ABCD 的底面 ABCD 是平 行四边形,BA=BD= 2,AD=2,PA=PD= 5,E,F 分别是棱 AD,PC 的中点. (1)证明:EF∥平面 PAB; (2)若二面角 PADB 为 60°. (i)证明:平面 PBC⊥平面 ABCD; (ii)求直线 EF 与平面 PBC 所成角的正弦值. 17.解:(1)证明:如图所示,取 PB 中点 M,连接 MF,AM.因为 F 为 PC 中点,所以 MF∥BC,且 MF=1 2BC.由已知有 BC∥AD,BC=AD,又由于 E 为 AD 中点,因而 MF∥AE 且 MF=AE,故四边形 AMFE 为平行四边形,所以 EF∥AM.又 AM⊂平面 PAB,而 EF⊄平面 PAB,所以 EF∥平面 PAB. (2)(i)证明:连接 PE,BE.因为 PA=PD,BA=BD,而 E 为 AD 中点,所以 PE⊥AD, BE⊥AD,所以∠PEB 为二面角 P AD B 的平面角.在△PAD 中,由 PA=PD= 5,AD=2, 可解得 PE=2.在△ABD 中,由 BA=BD= 2,AD=2,可解得 BE=1.在△PEB 中,PE=2, BE=1,∠PEB=60˚,由余弦定理,可解得 PB= 3,从而∠PBE=90˚,即 BE⊥PB.又 BC∥AD, BE⊥AD,从而 BE⊥BC,因此 BE⊥平面PBC.又BE⊂平面 ABCD,所以平面PBC⊥平面ABCD. (ii)连接 BF,由(i)知,BE⊥平面 PBC,所以∠EFB 为直线 EF 与平面 PBC 所成的角.由 PB= 3及已知,得∠ABP 为直角,而 MB=1 2PB= 3 2 ,可得 AM= 11 2 ,故 EF= 11 2 .又 BE =1,故在直角三角形 EBF 中,sin∠EFB=BE EF =2 11 11 .所以直线 EF 与平面 PBC 所成角的正 弦值为2 11 11 . 20.G5、G11[2014·浙江卷] 如图 15,在四棱锥 A BCDE 中,平面 ABC⊥平面 BCDE, ∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 2. 图 15 (1)证明:AC⊥平面 BCDE; (2)求直线 AE 与平面 ABC 所成的角的正切值. 20.解:(1)证明:连接 BD,在直角梯形 BCDE 中,由 DE=BE=1,CD=2,得 BD= BC= 2,由 AC= 2,AB=2,得 AB2=AC2+BC2,即 AC⊥BC. 又平面 ABC⊥平面 BCDE,从而 AC⊥平面 BCDE. (2)在直角梯形 BCDE 中,由 BD=BC= 2,DC=2,得 BD⊥BC. 又平面 ABC⊥平面 BCDE,所以 BD⊥平面 ABC. 作 EF∥BD,与 CB 的延长线交于点 F,连接 AF,则 EF⊥平面 ABC. 所以∠EAF 是直线 AE 与平面 ABC 所成的角. 在 Rt△BEF 中,由 EB=1,∠EBF=π 4 ,得 EF= 2 2 ,BF= 2 2 ; 在 Rt△ACF 中,由 AC= 2,CF=3 2 2 , 得 AF= 26 2 . 在 Rt△AEF 中,由 EF= 2 2 ,AF= 26 2 , 得 tan∠EAF= 13 13 . 所以,直线 AE 与平面 ABC 所成的角的正切值是 13 13 . 20.G1、G5[2014·重庆卷] 如图 14 所示四棱锥 PABCD 中,底面是以 O 为中心的菱 形,PO⊥底面 ABCD,AB=2,∠BAD=π 3 ,M 为 BC 上一点, 且 BM=1 2. (1)证明:BC⊥平面 POM; (2)若 MP⊥AP,求四棱锥 PABMO 的体积. 图 14 20.解:(1)证明:如图所示,因为四边形 ABCD 为菱形,O 为菱形的中心,连接 OB, 则 AO⊥OB.因为∠BAD=π 3 ,所以 OB=AB·sin∠OAB=2sinπ 6 =1. 又因为 BM=1 2 ,且∠OBM=π 3 ,在△OBM 中,OM2=OB2+BM2-2OB·BM·cos∠OBM =12+ 1 2 2 -2×1×1 2 ×cosπ 3 =3 4 ,所以 OB2=OM2+BM2,故 OM⊥BM. 又 PO⊥底面 ABCD,所以 PO⊥BC.从而 BC 与平面 POM 内的两条相交直线 OM,PO 都垂直,所以 BC⊥平面 POM. (2)由(1)可得,OA=AB·cos∠OAB=2×cosπ 6 = 3. 设 PO=a,由 PO⊥底面 ABCD,知△POA 为直角三角形,故 PA2=PO2+OA2=a2+3. 又△POM 也是直角三角形,故 PM2=PO2+OM2=a2+3 4.连接 AM,在△ABM 中,AM2 =AB2+BM2-2AB·BM·cos∠ABM=22+ 1 2 2 -2×2×1 2 ×cos2π 3 =21 4 . 由已知 MP⊥AP,故△APM 为直角三角形,则 PA2+PM2=AM2,即 a2+3+a2+3 4 =21 4 , 解得 a= 3 2 或 a=- 3 2 (舍去),即 PO= 3 2 . 此时 S 四边形 ABMO=S△AOB+S△OMB =1 2 ·AO·OB+1 2 ·BM·OM =1 2 × 3×1+1 2 ×1 2 × 3 2 =5 3 8 . 所以四棱锥 PABMO 的体积 V 四棱锥 PABMO=1 3 ·S 四边形 ABMO·PO=1 3 ×5 3 8 × 3 2 = 5 16. G6 三垂线定理 19.G6、G11[2014·全国卷] 如图 11 所示,三棱柱 ABC A1B1C1 中,点 A1 在平面 ABC 内的射影 D 在 AC 上,∠ACB=90°,BC=1,AC=CC1=2. (1)证明:AC1⊥A1B; (2)设直线 AA1 与平面 BCC1B1 的距离为 3,求二面角 A1 AB C 的大小. 图 11 19.解:方法一:(1)证明:因为 A1D⊥平面 ABC,A1D⊂平面 AA1C1C,故平面 AA1C1C ⊥平面 ABC.又 BC⊥AC,平面 AA1C1C∩平面 ABC=AC,所以 BC⊥平面 AA1C1C. 连接 A1C,因为侧面 AA1C1C 为菱形,故 AC1⊥A1C. 由三垂线定理得 AC1⊥A1B. (2)BC⊥平面 AA1C1C,BC⊂平面 BCC1B1, 故平面 AA1C1C⊥平面 BCC1B1. 作 A1E⊥CC1,E 为垂足,则 A1E⊥平面 BCC1B1. 又直线 AA1∥平面 BCC1B1,因而 A1E 为直线 AA1 与平面 BCC1B1 的距离,即 A1E= 3. 因为 A1C 为∠ACC1 的平分线,故 A1D=A1E= 3. 作 DF⊥AB,F 为垂足,连接 A1F.由三垂线定理得 A1F⊥AB, 故∠A1FD 为二面角 A1 AB C 的平面角. 由 AD= AA21-A1D2=1,得 D 为 AC 中点, 所以 DF= 5 5 ,tan∠A1FD=A1D DF = 15, 所以 cos∠A1FD=1 4. 所以二面角 A1 AB C 的大小为 arccos1 4. 方法二:以 C 为坐标原点,射线 CA 为 x 轴的正半轴,以 CB 的长为单位长,建立如图 所示的空间直线坐标系 C xyz.由题设知 A1D 与 z 轴平行,z 轴在平面 AA1C1C 内. (1)证明:设 A1(a,0,c),由题设有 a≤2,A(2,0,0),B(0,1,0),则AB→=(-2,1, 0),AC→=(-2,0,0),AA1 → =(a-2,0,c),AC1 → =AC→+AA1 → =(a-4,0,c),BA1 → =(a,-1, c). 由|AA1 → |=2,得 (a-2)2+c2=2,即 a2-4a+c2=0. ① 又AC1 → ·BA1 → =a2-4a+c2=0,所以 AC1⊥A1B. (2)设平面 BCC1B1 的法向量 m=(x,y,z), 则 m⊥CB→,m⊥BB1 → ,即 m·CB=0,m·BB1 → =0. 因为CB→=(0,1,0),BB1 → =AA1 → =(a-2,0,c),所以 y=0,且(a-2)x+cz=0. 令 x=c,则 z=2-a,所以 m=(c,0,2-a),故点 A 到平面 BCC1B1 的距离为|CA→|·|cos 〈m,CA→〉|=|CA→·m| |m| = 2c c2+(2-a)2 =c. 又依题设,A 到平面 BCC1B1 的距离为 3, 所以 c= 3, 代入①,解得 a=3(舍去)或 a=1, 于是AA1 → =(-1,0, 3). 设平面 ABA1 的法向量 n=(p,q,r),则 n⊥AA1 → ,n⊥AB→,即 n·AA1 → =0,n·AB→=0, 所以-p+ 3r=0,且-2p+q=0.令 p= 3,则 q=2 3,r=1,所以 n=( 3,2 3, 1). 又 p=(0,0,1)为平面 ABC 的法向量,故 cos〈n,p〉= n·p |n||p| =1 4 , 所以二面角 A1 AB C 的大小为 arccos1 4. G7 棱柱与棱锥 19.G5,G7[2014·福建卷] 如图 16 所示,三棱锥 A BCD 中,AB⊥平面 BCD,CD ⊥BD. (1)求证:CD⊥平面 ABD; (2)若 AB=BD=CD=1,M 为 AD 中点,求三棱锥 A MBC 的体积. 图 16 19.解:方法一:(1)证明:∵AB⊥平面 BCD,CD⊂平面 BCD, ∴AB⊥CD. 又∵CD⊥BD,AB∩BD=B, AB⊂平面 ABD,BD⊂平面 ABD, ∴CD⊥平面 ABD. (2)由 AB⊥平面 BCD, 得 AB⊥BD. ∵AB=BD=1,∴S△ABD=1 2. ∵M 是 AD 的中点, ∴S△ABM=1 2S△ABD=1 4. 由(1)知,CD⊥平面 ABD, ∴三棱锥 C ABM 的高 h=CD=1, 因此三棱锥 A MBC 的体积 VA MBC=VC ABM=1 3S△ABM·h= 1 12. 方法二:(1)同方法一. (2)由 AB⊥平面 BCD,得平面 ABD⊥平面 BCD. 且平面 ABD∩平面 BCD=BD. 如图所示,过点 M 作 MN⊥BD 交 BD 于点 N, 则 MN⊥平面 BCD,且 MN=1 2AB=1 2. 又 CD⊥BD,BD=CD=1,∴S△BCD=1 2. ∴三棱锥 A MBC 的体积 VA MBC=VA BCD-VM BCD =1 3AB·S△BCD-1 3MN·S△BCD = 1 12. 18.G5、G7[2014·广东卷] 如图 12 所示,四边形 ABCD 为矩形,PD⊥平面 ABCD, AB=1,BC=PC=2,作如图 13 折叠:折痕 EF∥DC,其中点 E,F 分别在线段 PD,PC 上,沿 EF 折叠后点 P 叠在线段 AD 上的点记为 M,并且 MF⊥CF. (1)证明:CF⊥平面 MDF; (2)求三棱锥 M CDE 的体积. 图 12 图 13 8.G7[2014·江苏卷] 设甲、乙两个圆柱的底面积分别为 S1,S2,体积分别为 V1,V2.若 它们的侧面积相等,且S1 S2 =9 4 ,则V1 V2 的值是________. 8.3 2 [解析] 因为S1 S2 =πr21 πr22 =r21 r22 =9 4 ,所以r1 r2 =3 2.又圆柱的侧面积 S 侧=2πrh,所以 S 侧 1=2 πr1h1=S 侧 2=2πr2h2,则h1 h2 =r2 r1 =2 3 ,故V1 V2 =S1h1 S2h2 =9 4 ×2 3 =3 2. 19.G5、G7[2014·江西卷] 如图 11 所示,三棱柱 ABC A1B1C1 中,AA1⊥BC,A1B⊥ BB1. (1)求证:A1C⊥CC1; (2)若 AB=2,AC= 3,BC= 7,问 AA1 为何值时,三棱柱 ABC A1B1C1 体积最大,并 求此最大值. 图 11 19.解:(1)证明:由 AA1⊥BC 知 BB1⊥BC.又 BB1⊥A1B,故 BB1⊥平面 BCA1,所以 BB1 ⊥A1C. 又 BB1∥CC1,所以 A1C⊥CC1. (2)方法一:设 AA1=x. 在 Rt△A1BB1 中,A1B= A1B21-BB21= 4-x2. 同理,A1C= A1C21-CC21= 3-x2. 在△A1BC 中, cos∠BA1C=A1B2+A1C2-BC2 2A1B·A1C = - x2 (4-x2)(3-x2) , sin∠BA1C= 12-7x2 (4-x2)(3-x2) , 所以 S△A1BC=1 2A1B·A1C·sin∠BA1C= 12-7x2 2 . 从而三棱柱 ABC A1B1C1 的体积 V=S 直·l=S△A1BC·AA1=x 12-7x2 2 . 因为 x 12-7x2= 12x2-7x4= -7 x2-6 7 2 +36 7 , 所以当 x= 6 7 = 42 7 ,即 AA1= 42 7 时,体积 V 取到最大值3 7 7 . (2)方法二:过 A1 作 BC 的垂线,垂足为 D,连接 AD. 由 AA1⊥BC,A1D⊥BC,得 BC⊥平面 AA1D,故 BC⊥AD.又∠BAC=90°, 所以 S△ABC=1 2AD·BC=1 2AB·AC,得 AD=2 21 7 . 设 AA1=x.在 Rt△AA1D 中, A1D= AD2-AA21= 12 7 -x2, S△A1BC=1 2A1D·BC= 12-7x2 2 . 从而三棱柱 ABC A1B1C1 的体积 V=S 直·l=S△A1BC·AA1=x 12-7x2 2 .因为 x 12-7x2 = 12x2-7x4= -7 x2-6 7 2 +36 7 , 所以当 x= 6 7 = 42 7 ,即 AA1= 42 7 时,体积 V 取到最大值3 7 7 . 7.G2、G7[2014·辽宁卷] 某几何体三视图如图 12 所示,则该几何体的体积为( ) 图 12 A.8-π 4 B.8-π 2 C.8-π D.8-2π 7.C [解析] 根据三视图可知,该几何体是正方体切去两个体积相等的圆柱的四分之 一后余下的部分,故该几何体体积 V=23-1 2 ×π×12×2=8-π. 19.G5、G7[2014·辽宁卷] 如图 14 所示,△ABC 和△BCD 所在平面互相垂直,且 AB =BC=BD=2,∠ABC=∠DBC=120°,E,F,G 分别为 AC,DC,AD 的中点. 图 14 (1)求证:EF⊥平面 BCG; (2)求三棱锥 D BCG 的体积. 附:锥体的体积公式 V=1 3Sh,其中 S 为底面面积,h 为高. 19.解:(1)证明:由已知得△ABC≌△DBC, 因此 AC=DC. 又 G 为 AD 的中点,所以 CG⊥AD, 同理 BG⊥AD.又 BG∩CG=G,所以 AD⊥平面 BGC. 又 EF∥AD,所以 EF⊥平面 BCG. (2)在平面 ABC 内,作 AO⊥CB,交 CB 延长线于点 O. 由平面 ABC⊥平面 BCD,知 AO⊥平面 BDC. 又 G 为 AD 的中点,所以 G 到平面 BDC 的距离 h 是 AO 长度的一半. 在△AOB 中,AO=AB·sin 60°= 3,所以 V 三棱锥 D BCG=V 三棱锥 G BCD=1 3 ·S△DBC·h=1 3 ×1 2 ·BD·BC·sin 120°· 3 2 =1 2. 10.G7、G8[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为 4,底面 边长为 2,则该球的表面积为( ) A.81π 4 B.16π C.9π D.27π 4 10.A [解析] 如图所示,因为正四棱锥的底面边长为 2,所以 AE=1 2AC= 2.设球心 为 O,球的半径为 R,则 OE=4-R,OA=R.又因为△AOE 为直角三角形,所以 OA2=OE2 +AE2,即 R2=(4-R)2+2,解得 R=9 4 ,所以该球的表面积 S=4πR2=4π 9 4 2=81π 4 . 13.G7[2014·山东卷] 一个六棱锥的体积为 2 3,其底面是边长为 2 的正六边形,侧棱 长都相等,则该六棱锥的侧面积为________. 13.12 [解析] 设该六棱锥的高是 h.根据体积公式得,V=1 3 ×1 2 ×2× 3×6×h,解得 h=1,则侧面三角形的高为 1+( 3)2=2,所以侧面积 S=1 2 ×2×2×6=12. G8 多面体与球 8.G2、G8[2014·湖南卷] 一块石材表示的几何体的三视图如图 12 所示,将该石材切 削、打磨,加工成球,则能得到的最大球的半径等于( ) 图 12 A.1 B.2 C.3 D.4 8.B [解析] 由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得 到的最大球为三棱柱的内切球.由题意可知正视图三角形的内切圆的半径即为球的半径,可 得 R=6+8-10 2 =2. 5.G8[2014·陕西卷] 将边长为 1 的正方形以其一边所在直线为旋转轴旋转一周,所得 几何体的侧面积是( ) A.4π B.3π C.2π D.π 5.C [解析] 由题意可知,旋转体是一个底面半径为 1,高为 1 的圆柱,故其侧面积 为 2π×1×1=2π. 10.G7、G8[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为 4,底面 边长为 2,则该球的表面积为( ) A.81π 4 B.16π C.9π D.27π 4 10.A [解析] 如图所示,因为正四棱锥的底面边长为 2,所以 AE=1 2AC= 2.设球心 为 O,球的半径为 R,则 OE=4-R,OA=R.又因为△AOE 为直角三角形,所以 OA2=OE2 +AE2,即 R2=(4-R)2+2,解得 R=9 4 ,所以该球的表面积 S=4πR2=4π 9 4 2=81π 4 . 17.G2、G8[2014·陕西卷] 四面体 ABCD 及其三视图如图 14 所示,平行于棱 AD,BC 的平面分别交四面体的棱 AB,BD,DC,CA 于点 E,F,G,H. 图 14 (1)求四面体 ABCD 的体积; (2)证明:四边形 EFGH 是矩形. 17.解:(1)由该四面体的三视图可知, BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1, ∴AD⊥平面 BDC, ∴四面体 ABCD 的体积 V=1 3 ×1 2 ×2×2×1=2 3. (2)证明:∵BC∥平面 EFGH,平面 EFGH∩平面 BDC=FG,平面 EFGH∩ 平面 ABC =EH, ∴BC∥FG,BC∥EH,∴FG∥EH. 同理 EF∥AD,HG∥AD,∴EF∥HG, ∴四边形 EFGH 是平行四边形. 又∵AD⊥平面 BDC,∴AD⊥BC,∴EF⊥FG, ∴四边形 EFGH 是矩形. G9 空间向量及运算 G10 空间向量解决线面位置关系 G11 空间角与距离的求法 10.G11[2014·浙江卷] 如图 13,某人在垂直于水平地面 ABC 的墙面前的点 A 处进行 射击训练.已知点 A 到墙面的距离为 AB,某目标点 P 沿墙面上的射线 CM 移动,此人为了 准确瞄准目标点 P,需计算由点 A 观察点 P 的仰角θ的大小(仰角θ为直线 AP 与平面 ABC 所 成角).若 AB=15 m,AC=25 m,∠BCM=30°,则 tan θ的最大值是( ) 图 13 A. 30 5 B. 30 10 C.4 3 9 D.5 3 9 10.D [解析] 由勾股定理得 BC=20 m.如图,过 P 点作 PD⊥BC 于 D,连接 AD, 则由点 A 观察点 P 的仰角θ=∠PAD,tan θ=PD AD.设 PD=x,则 DC= 3x,BD=20- 3x, 在 Rt △ ABD 中 , AD = 152+(20- 3x)2 = 625-40 3x+3x2 , 所 以 tan θ = x 625-40 3x+3x2 = 1 625 x2 -40 3 x +3 = 1 625 1 x -20 3 625 2 +27 25 ≤5 3 9 ,故 tan θ的最大值 为5 3 9 ,故选 D. 4.G11[2014·全国卷] 已知正四面体 ABCD 中,E 是 AB 的中点,则异面直线 CE 与 BD 所成角的余弦值为( ) A.1 6 B. 3 6 C.1 3 D. 3 3 4.B [解析] 如图所示,取 AD 的中点 F,连接 EF,CF,则 EF∥BD,故 EF 与 CE 所成的角即为异面直线 CE 与 BD 所成的角.设正四面体的棱长为 2,则 CE=CF= 3,EF =1.在△CEF 中,cos ∠CEF=CE2+EF2-CF2 2CE·EF = 3+1-3 2× 3×1 = 3 6 ,所以异面直线 CE 与 BD 所成角的余弦值为 3 6 . 19.G6、G11[2014·全国卷] 如图 11 所示,三棱柱 ABC A1B1C1 中,点 A1 在平面 ABC 内的射影 D 在 AC 上,∠ACB=90°,BC=1,AC=CC1=2. (1)证明:AC1⊥A1B; (2)设直线 AA1 与平面 BCC1B1 的距离为 3,求二面角 A1 AB C 的大小. 图 11 19.解:方法一:(1)证明:因为 A1D⊥平面 ABC,A1D⊂平面 AA1C1C,故平面 AA1C1C ⊥平面 ABC.又 BC⊥AC,平面 AA1C1C∩平面 ABC=AC,所以 BC⊥平面 AA1C1C. 连接 A1C,因为侧面 AA1C1C 为菱形,故 AC1⊥A1C. 由三垂线定理得 AC1⊥A1B. (2)BC⊥平面 AA1C1C,BC⊂平面 BCC1B1, 故平面 AA1C1C⊥平面 BCC1B1. 作 A1E⊥CC1,E 为垂足,则 A1E⊥平面 BCC1B1. 又直线 AA1∥平面 BCC1B1,因而 A1E 为直线 AA1 与平面 BCC1B1 的距离,即 A1E= 3. 因为 A1C 为∠ACC1 的平分线,故 A1D=A1E= 3. 作 DF⊥AB,F 为垂足,连接 A1F.由三垂线定理得 A1F⊥AB, 故∠A1FD 为二面角 A1 AB C 的平面角. 由 AD= AA21-A1D2=1,得 D 为 AC 中点, 所以 DF= 5 5 ,tan∠A1FD=A1D DF = 15, 所以 cos∠A1FD=1 4. 所以二面角 A1 AB C 的大小为 arccos1 4. 方法二:以 C 为坐标原点,射线 CA 为 x 轴的正半轴,以 CB 的长为单位长,建立如图 所示的空间直线坐标系 C xyz.由题设知 A1D 与 z 轴平行,z 轴在平面 AA1C1C 内. (1)证明:设 A1(a,0,c),由题设有 a≤2,A(2,0,0),B(0,1,0),则AB→=(-2,1, 0),AC→=(-2,0,0),AA1 → =(a-2,0,c),AC1 → =AC→+AA1 → =(a-4,0,c),BA1 → =(a,-1, c). 由|AA1 → |=2,得 (a-2)2+c2=2,即 a2-4a+c2=0. ① 又AC1 → ·BA1 → =a2-4a+c2=0,所以 AC1⊥A1B. (2)设平面 BCC1B1 的法向量 m=(x,y,z), 则 m⊥CB→,m⊥BB1 → ,即 m·CB=0,m·BB1 → =0. 因为CB→=(0,1,0),BB1 → =AA1 → =(a-2,0,c),所以 y=0,且(a-2)x+cz=0. 令 x=c,则 z=2-a,所以 m=(c,0,2-a),故点 A 到平面 BCC1B1 的距离为|CA→|·|cos 〈m,CA→〉|=|CA→·m| |m| = 2c c2+(2-a)2 =c. 又依题设,A 到平面 BCC1B1 的距离为 3, 所以 c= 3, 代入①,解得 a=3(舍去)或 a=1, 于是AA1 → =(-1,0, 3). 设平面 ABA1 的法向量 n=(p,q,r),则 n⊥AA1 → ,n⊥AB→,即 n·AA1 → =0,n·AB→=0, 所以-p+ 3r=0,且-2p+q=0.令 p= 3,则 q=2 3,r=1,所以 n=( 3,2 3, 1). 又 p=(0,0,1)为平面 ABC 的法向量,故 cos〈n,p〉= n·p |n||p| =1 4 , 所以二面角 A1 AB C 的大小为 arccos1 4. 18.G4、G11[2014·新课标全国卷Ⅱ] 如图 13,四棱锥 P ABCD 中,底面 ABCD 为矩 形,PA⊥平面 ABCD,E 为 PD 的中点. (1)证明:PB∥平面 AEC; (2)设 AP=1,AD= 3,三棱锥 P ABD 的体积 V= 3 4 ,求 A 到平面 PBC 的距离. 图 13 18.解:(1)证明:设 BD 与 AC 的交点为 O,连接 EO. 因为 ABCD 为矩形,所以 O 为 BD 的中点. 又 E 为 PD 的中点,所以 EO∥PB. EO⊂平面 AEC,PB⊄平面 AEC, 所以 PB∥平面 AEC. (2)V=1 3 ×1 2 ×PA×AB×AD= 3 6 AB, 由 V= 3 4 ,可得 AB=3 2. 作 AH⊥PB 交 PB 于点 H. 由题设知 BC⊥平面 PAB,所以 BC⊥AH, 因为 PB∩BC=B,所以 AH⊥平面 PBC. 又 AH=PA·AB PB =3 13 13 , 所以点 A 到平面 PBC 的距离为3 13 13 . 19.G5 G11[2014·全国新课标卷Ⅰ] 如图 14,三棱柱 ABC A1B1C1 中,侧面 BB1C1C 为菱形,B1C 的中点为 O,且 AO⊥平面 BB1C1C. 图 14 (1)证明:B1C⊥AB; (2)若 AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱 ABC A1B1C1 的高. 19.解:(1)证明:连接 BC1,则 O 为 B1C 与 BC1 的交点. 因为侧面 BB1C1C 为菱形,所以 B1C⊥BC1. 又 AO⊥平面 BB1C1C,所以 B1C⊥AO, 由于 BC1∩AO=O,故 B1C⊥平面 ABO. 由于 AB⊂平面 ABO,故 B1C⊥AB. (2)作 OD⊥BC,垂足为 D,连接 AD.作 OH⊥AD,垂足为 H. 由于 BC⊥AO,BC⊥OD,且 AO∩OD=O, 故 BC⊥平面 AOD,所以 OH⊥BC. 又 OH⊥AD,且 AD∩BC=D, 所以 OH⊥平面 ABC. 因为∠CBB1=60°,所以△CBB1 为等边三角形,又 BC=1,可得 OD= 3 4 . 因为 AC⊥AB1,所以 OA=1 2B1C=1 2. 由 OH·AD=OD·OA,且 AD= OD2+OA2= 7 4 ,得 OH= 21 14 . 又 O 为 B1C 的中点,所以点 B1 到平面 ABC 的距离为 21 7 .故三棱柱 ABC A1B1C1 的高为 21 7 . 17.G4、G5、G11[2014·天津卷] 如图 14 所示,四棱锥 P ABCD 的底面 ABCD 是平 行四边形,BA=BD= 2,AD=2,PA=PD= 5,E,F 分别是棱 AD,PC 的中点. (1)证明:EF∥平面 PAB; (2)若二面角 PADB 为 60°. (i)证明:平面 PBC⊥平面 ABCD; (ii)求直线 EF 与平面 PBC 所成角的正弦值. 17.解:(1)证明:如图所示,取 PB 中点 M,连接 MF,AM.因为 F 为 PC 中点,所以 MF∥BC,且 MF=1 2BC.由已知有 BC∥AD,BC=AD,又由于 E 为 AD 中点,因而 MF∥AE 且 MF=AE,故四边形 AMFE 为平行四边形,所以 EF∥AM.又 AM⊂平面 PAB,而 EF⊄平面 PAB,所以 EF∥平面 PAB. (2)(i)证明:连接 PE,BE.因为 PA=PD,BA=BD,而 E 为 AD 中点,所以 PE⊥AD, BE⊥AD,所以∠PEB 为二面角 P AD B 的平面角.在△PAD 中,由 PA=PD= 5,AD=2, 可解得 PE=2.在△ABD 中,由 BA=BD= 2,AD=2,可解得 BE=1.在△PEB 中,PE=2, BE=1,∠PEB=60˚,由余弦定理,可解得 PB= 3,从而∠PBE=90˚,即 BE⊥PB.又 BC∥AD, BE⊥AD,从而 BE⊥BC,因此 BE⊥平面PBC.又BE⊂平面 ABCD,所以平面PBC⊥平面ABCD. (ii)连接 BF,由(i)知,BE⊥平面 PBC,所以∠EFB 为直线 EF 与平面 PBC 所成的角.由 PB= 3及已知,得∠ABP 为直角,而 MB=1 2PB= 3 2 ,可得 AM= 11 2 ,故 EF= 11 2 .又 BE =1,故在直角三角形 EBF 中,sin∠EFB=BE EF =2 11 11 .所以直线 EF 与平面 PBC 所成角的正 弦值为2 11 11 . 20.G5、G11[2014·浙江卷] 如图 15,在四棱锥 A BCDE 中,平面 ABC⊥平面 BCDE, ∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 2. 图 15 (1)证明:AC⊥平面 BCDE; (2)求直线 AE 与平面 ABC 所成的角的正切值. 20.解:(1)证明:连接 BD,在直角梯形 BCDE 中,由 DE=BE=1,CD=2,得 BD= BC= 2,由 AC= 2,AB=2,得 AB2=AC2+BC2,即 AC⊥BC. 又平面 ABC⊥平面 BCDE,从而 AC⊥平面 BCDE. (2)在直角梯形 BCDE 中,由 BD=BC= 2,DC=2,得 BD⊥BC. 又平面 ABC⊥平面 BCDE,所以 BD⊥平面 ABC. 作 EF∥BD,与 CB 的延长线交于点 F,连接 AF,则 EF⊥平面 ABC. 所以∠EAF 是直线 AE 与平面 ABC 所成的角. 在 Rt△BEF 中,由 EB=1,∠EBF=π 4 ,得 EF= 2 2 ,BF= 2 2 ; 在 Rt△ACF 中,由 AC= 2,CF=3 2 2 , 得 AF= 26 2 . 在 Rt△AEF 中,由 EF= 2 2 ,AF= 26 2 , 得 tan∠EAF= 13 13 . 所以,直线 AE 与平面 ABC 所成的角的正切值是 13 13 . G12 单元综合 8.[2014·江西师大附中、临川一中期末] 如图 X2310 所示,三棱锥 S ABC 中,SA= AB=AC=2,∠ASB=∠BSC=∠CSA=30°,M,N 分别为 SB,SC 上的点,则△AMN 的 周长的最小值为________. 图 X2310 8.2 2 [解析] 展开三棱锥的侧面如图所示.因为∠ASB=∠BSC=∠CSA=30°, SA=AB=AC=2,所以△ASA′是等腰直角三角形,连接 AA′可得△AMN 的周长的最小值为 2 2. 2.[2014·常德期末] 若某空间几何体的三视图如图 X242 所示,则该几何体的表面积 是( ) A.60 B.54 C.48 D.24 图 X242 2.A [解析] 由三视图可知,原几何体是一个三棱柱,依据所给数据,可求得其表面 积 S=(3+4+5)×4+2×1 2 ×4×3=60. 5.[2014·衡阳八中月考] 一个棱长为 2 的正方体被一个平面截后所得几何体的三视图如 图 X245 所示,则该几何体的体积是( ) A.8 B.20 3 C.17 3 D.14 3 图 X245 5.C [解析] 该几何体是由正方体截去一个三棱台得到的,则所求体积 V=23-1 3 ×1 2 + 2+ 2×1 2 ×2=17 3 . 3.[2014·咸阳模拟] 设α,β是两个不同的平面,l 是一条直线,给出下列说法: ①若 l⊥α,α⊥β,则 l⊂β;②若 l∥α,α∥β,则 l⊂β; ③若 l⊥α,α∥β,则 l⊥β;④若 l∥α,α⊥β,则 l⊥β. 其中说法正确的个数为( ) A.1 B.2 C.3 D.0 3.A [解析] 对于①,若 l⊥α,α⊥β,则 l∥β或 l⊂β,故①错误;对于②,若 l∥α, α∥β,则 l⊂β或 l∥β,故②错误;对于③,若 l⊥α,α∥β,则 l⊥β,故③正确;对于 ④,若 l∥α,α⊥β,则 l⊂β或 l∥β或 l⊥β或 l 与β斜交,故④错误. 10.[2014·景德镇质检] 如图 X252 所示,在正方体 ABCD A1B1C1D1 中,M,N 分别 是棱 C1D1,C1C 的中点,给出以下四个结论: ①直线 AM 与直线 C1C 相交; ②直线 AM 与直线 BN 平行; ③直线 AM 与直线 DD1 异面; ④直线 BN 与直线 MB1 异面. 其中正确结论的序号为________.(把你认为正确的结论的序号都填上) 图 X252 10.③④ [解析] AM 与 C1C 异面,故①错;AM 与 BN 异面,故②错.易知③④正确. 1.[2014·济南期末] 如图 J121 所示,在四棱锥 P ABCD 中,PA⊥平面 ABCD,AD⊥AB, △ABC 是正三角形,AC 与 BD 的交点 M 恰好是 AC 的中点,N 为线段 PB 的中点,G 在线 段 BM 上,且BG GM =2. (1)求证:AB⊥PD; (2)求证:GN∥平面 PCD. 图 J121 1.证明:(1)因为 PA⊥平面 ABCD,所以 PA⊥AB. 又因为 AD⊥AB,AD∩PA=A,所以 AB⊥平面 PAD. 又 PD⊂平面 PAD,所以 AB⊥PD. (2)因为△ABC 是正三角形,且 M 是 AC 的中点, 所以 BM⊥AC. 在直角三角形 AMD 中,∠MAD=30°,所以 MD=1 2AD. 在直角三角形 ABD 中,∠ABD=30°, 所以 AD=1 2BD,所以 MD=1 4BD. 又因为BG GM =2,所以 BG=GD. 又 N 为线段 PB 的中点,所以 GN∥PD. 又 GN⊄平面 PCD,PD⊂平面 PCD,所以 GN∥平面 PCD. 2.[2014·温州一模] 如图 J132 所示,平面 ABEF⊥平面 ABC,四边形 ABEF 为矩形, 且 AC=BC,O 为 AB 的中点,OF⊥EC. (1)求证:OE⊥FC; (2)若 FC 与平面 ABC 所成的角为 30°,求二面角 F CE B 的余弦值. 图 J132 2.解:(1)证明:连接 OC,因为 AC=BC,O 是 AB 的中点, 所以 OC⊥AB. 又因为平面 ABC⊥平面 ABEF, 平面 ABC∩平面 ABEF=AB, 所以 OC⊥平面 ABEF,于是 OC⊥OF. 又 OF⊥EC,EC∩OC=C, 所以 OF⊥平面 OEC,所以 OF⊥OE. 又因为 OC⊥OE,OC∩OF=O, 所以 OE⊥平面 OFC, 所以 OE⊥FC. (2)方法一:由(1),得 AB=2AF.不妨设 AF=1,AB=2. 因为∠FCA 为直线 FC 与平面 ABC 所成的角, 所以∠FCA=30°, 所以 FC=EC=2,△EFC 为等边三角形. 设 FO∩EB=P,则 O,B 分别为 PF,PE 的中点,△PEC 也是等边三角形. 取 EC 的中点 M,连接 FM,MP,则 FM⊥CE,MP⊥CE, 所以∠FMP 为二面角 F CE B 的平面角. 在△MFP 中,FM=MP= 3,FP=2 2, 故 cos∠FMP=FM2+MP2-FP2 2FM·MP = 3+3-8 2× 3× 3 =-1 3 , 即二面角 F CE B 的余弦值为-1 3. 方法二:取 EF 的中点 D,以 O 为原点,分别以 OC,OB,OD 所在直线为 x 轴、y 轴、 z 轴建立如图所示的空间直角坐标系 O xyz.不妨设 AF=1,AB=2,则 B(0,1,0),C( 2, 0,0),E(0,1,1),F(0,-1,1), 从而CE→=(- 2,1,1),EF→=(0,-2,0). 设平面 FCE 的法向量为 n1=(x1,y1,z1), 由 EC→·n1=0, EF→·n1=0, 得 - 2x1+y1+z1=0, -2y1=0, 可取 n1=(1,0, 2). 同理,可取平面 BEC 的一个法向量为 n2=(1,2,0), 于是 cos〈n1,n2〉=n1·n2 |n1||n2| =1 3. 易知二面角 F EC B 的平面角与〈n1,n2〉互补, 所以二面角 F EC B 的余弦值为-1 3.查看更多