- 2021-06-08 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021版高考数学一轮复习第二章函数及其应用2-5对数与对数函数练习苏教版
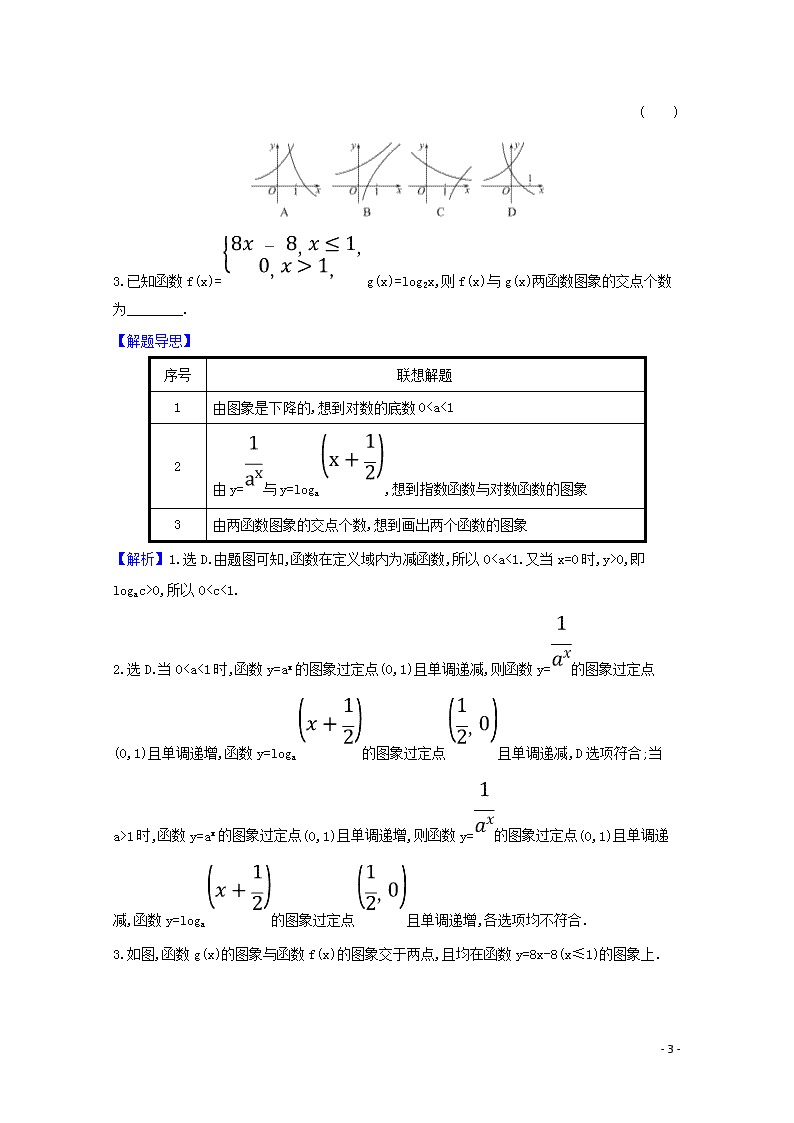
- 1 - 2.5 对数与对数函数 考点一 对数式的化简与求值 1.(2019·北京高考)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与 亮度满足 m2-m1= lg ,其中星等为 mk 的星的亮度为 Ek(k=1,2).已知太阳的星等是-26.7,天 狼星的星等是-1.45,则太阳与天狼星的亮度的比值为 ( ) A.1010.1 B.10.1 C.lg 10.1 D.10-10.1 2.(2020·苏州模拟)设函数 y=f(x)的图象与 y=2x+a 的图象关于直线 y=-x 对称,且 f(-2)+f(-4)=1,则 a= ( ) A.-1 B.1 C.2 D.4 3.设 x,y,z 为正数,且 2x=3y=5z,则 ( ) A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z 4.计算 log23·log38+( =________. 【解析】1.选 A.令 m1=-26.7,m2=-1.45, 则 m2-m1=-1.45-(-26.7)=25.25= lg , lg =10.1, =1010.1. 2.选 C.设(x,y)是函数 y=f(x)的图象上任意一点,它关于直线 y=-x 对称的点为(-y,-x), 由已知知(-y,-x)在函数 y=2x+a 的图象上, 所以-x=2-y+a,解得 y=-log2(-x)+a, 即 f(x)=-log2(-x)+a,所以 f(-2)+f(-4)=-log22+a-log24+a=1,解得 a=2,故选 C. - 2 - 3.选 D.令 2x=3y=5z=m,分别可求得 2x= = ,3y= = ,5z= = ,分别对分母乘以 30 可得,30logm =logm215,30logm =logm310,30logm =logm56, 故而可得 ⇒logm310>logm215>logm56⇒3y<2x<5z. 4.原式= · + =3+ =3+2=5. 答案:5 对数运算的一般思路 (1)将真数化为底数的指数幂的形式进行化简. (2)将同底对数的和、差、倍合并. (3)ab=N⇔b=logaN(a>0,且 a≠1)是解决有关指数、对数问题的有效方法,在运算中应注意互化. (4)利用换底公式将不同底的对数式转化为同底的对数式. 考点二 对数函数的图象及其应用 【典例】1.已知函数 y=loga(x+c)(a,c 为常数,其中 a>0,且 a≠1)的图象如图,则下列结论成 立的是 ( ) A.a>1,c>1 B.a>1,0查看更多