湖北省光谷第二高级中学高三物理 难点5 透视滑块与滑板等叠加体的相对运动（通用）

湖北省光谷第二高级中学高三物理 难点5 透视滑块与滑板等叠加体的相对运动（通用）

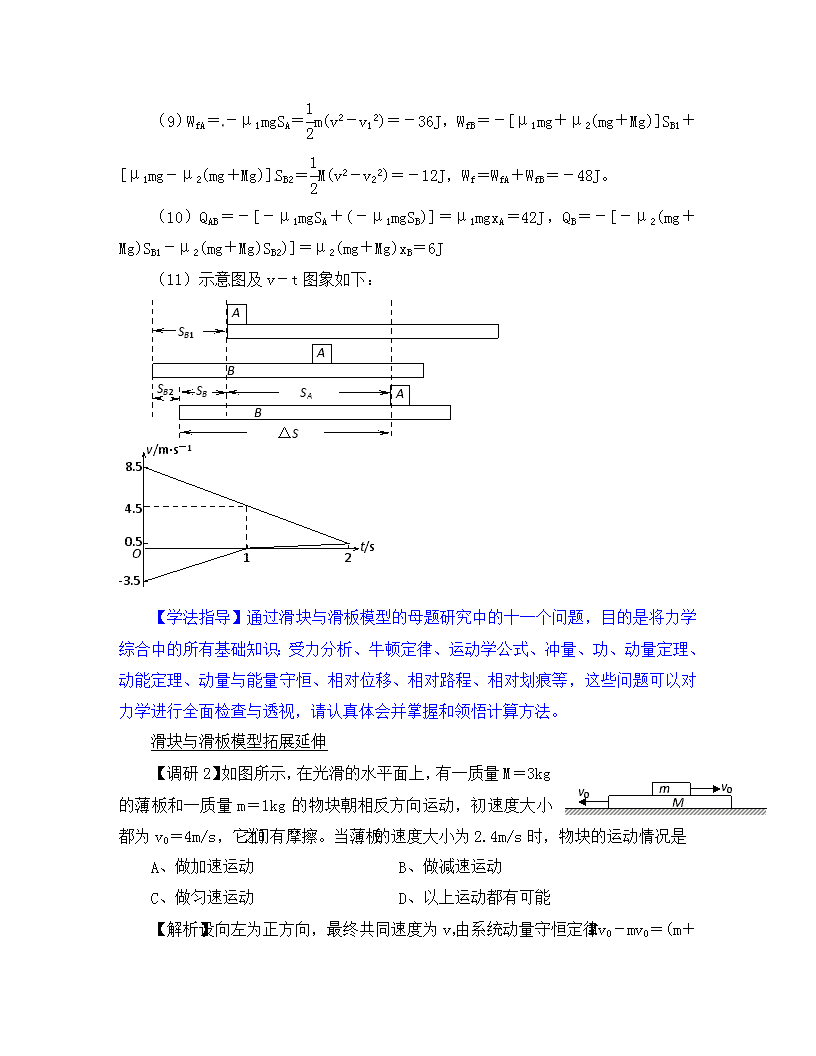
难点5 透视滑块与滑板等叠加体的相对运动（涉及到少数动量知识） ‎ 高中物理力学综合中的模型非常多，例如子弹打木块、碰撞（快速变力接触作用型，一个物体在另一个物体内部作用）、弹簧的连接体模型（中速变力、相对运动型，一个物体通过弹簧与另一个物体接触作用）、传送带滑块与滑板（慢速恒力、相对运动且相互作用型，一个物体与另一个物体相对运动）等。体现出难度大，知识点跨越运动定律、动量与能量、功能关系及能量守恒定律。总体来说，细节瞬间对受力分析要求较高，具有过程的矢量性与过程中动量与能量守恒。为了能够将众多的模型难度进行突破，我们选取其中最简单的滑块与滑板模型来研究，对受力分析、摩擦力分析、运动分析、位移分析、相对位移分析、划痕分析、相对路程分析、热量分析、图象分析及滑块滑板模型相对运动与相对静止的临界分析等进行全面透视。‎ 滑块与滑板模型母题探究 A B v1＝8.5m/s v2＝3.5m/s ‎【调研1】如图所示，滑块A的质量m＝1kg，初始速度向右v1＝8.5m/s；滑板B足够长，其质量M＝2kg，初始速度向左v2＝3.5m/s。已知滑块A与滑板B之间动摩擦因数μ1＝0.4，滑板B与地面之间动摩擦因数μ2＝0.1。取重力加速度g＝10m/s2。在两者相对运动的过程中：‎ 问题（1）：刚开始aA、aB1‎ 问题（2）：B向左运动的时间tB1及B向左运动的最大位移SB2‎ 问题（3）：两者相对静止时的速度v 问题（4）：A向右运动的时间t及A运动的位移SA 问题（5）：B运动的位移SB及B向右运动的时间tB2‎ 问题（6）：A对B的位移大小△S、A在B上的划痕△L、A在B上相对B运动的路程xA 问题（7）：B在地面的划痕LB、B在地面上的路程xB 问题（8）：摩擦力对A的冲量IfA、摩擦力对B的冲量IfB 、系统所有摩擦力对A和B的总冲量If 问题（9）：摩擦力对A做的功WfA、摩擦力对A做的功WfB、系统所有摩擦力对A和B的总功Wf 问题（10）：A、B间产生热量QAB、B与地面产生热量QB、系统因摩擦产生的热量Q 问题（11）：画出两者在相对运动过程中的示意图和v－t图象 ‎【解析】（1）由牛顿第二定律：aA＝＝μ1g＝4m/s，方向向左；aB1＝＝3.5m/s2，方向向右。‎ ‎（2）tB1＝＝1s，SB1＝＝1.75m，方向向左。‎ ‎（3）设向右为正方向，对A、B整体由动量守恒定律：mv1－Mv2＝(m＋M)v，解得v＝0.5m/s，方向向右。‎ ‎（4）t＝＝2s＞tB1＝1s，说明B先向左减速然后向右加速直到与A达到相同速度，A运动的位移SA＝＝9m ‎（5）B经过tB1＝1s后开始向右加速运动，达到v＝0.5m/s，加速度为aB2＝＝0.5m/s2，tB2＝＝1s，则向右运动的位移SB2＝＝0.25m，方向向右。故在两者相对运动过程中，B运动的总位移为SB＝SB1－SB2＝1.5m，方向向左。‎ ‎（6）△S＝SA＋SB＝10.5m，△L＝△S＝xA＝10.5m ‎（7）LB＝SB1＝1.75m，xB＝SB1＋SB2＝2m ‎（8）IfA＝μ1mgt＝m(v－v1)＝－8N·s，方向向左；IfB＝[μ1mg＋μ2(mg＋Mg)]tB1－[μ1mg－μ2(mg＋Mg)]tB2＝M(v＋v2)＝8N·s，方向向右；If＝IfA＋IfB＝0。说明：B向左运动和向右运动的时间相同，故地面对B的摩擦力的冲量总和为零，导致系统所有摩擦力对A和B的总冲量为零。‎ ‎（9）WfA＝－μ1mgSA＝m(v2－v12)＝－36J，WfB＝－[μ1mg＋μ2(mg＋Mg)]SB1‎ ‎＋[μ1mg－μ2(mg＋Mg)]SB2＝M(v2－v22)＝－12J，Wf＝WfA＋WfB＝－48J。‎ ‎（10）QAB＝－[－μ1mgSA＋(－μ1mgSB)]＝μ1mgxA＝42J，QB＝－[－μ2(mg＋Mg)SB1－μ2(mg＋Mg)SB2)]＝μ2(mg＋Mg)xB＝6J ‎（11）示意图及v－t图象如下：‎ SB1‎ A B A B A SB2‎ SA ‎△S SB v/m·s－1‎ t/s O ‎8.5‎ ‎0.5‎ ‎-3.5‎ ‎1‎ ‎2‎ ‎4.5‎ ‎【学法指导】通过滑块与滑板模型的母题研究中的十一个问题，目的是将力学综合中的所有基础知识：受力分析、牛顿定律、运动学公式、冲量、功、动量定理、动能定理、动量与能量守恒、相对位移、相对路程、相对划痕等，这些问题可以对力学进行全面检查与透视，请认真体会并掌握和领悟计算方法。‎ 滑块与滑板模型拓展延伸 v0‎ M v0‎ m ‎【调研2】如图所示，在光滑的水平面上，有一质量M＝‎3kg的薄板和一质量m＝‎1kg的物块朝相反方向运动，初速度大小都为v0＝‎4m/s，它们之间有摩擦。当薄板的速度大小为‎2.4m/s时，物块的运动情况是 A、做加速运动 B、做减速运动 C、做匀速运动 D、以上运动都有可能 ‎【解析】设向左为正方向，最终共同速度为v，由系统动量守恒定律：Mv0－mv0＝(m＋M)v，解得v＝2m/s，方向向左。当m的速度为零时，系统动量守恒定律：Mv0‎ ‎－mv0＝Mv1，解得M的速度为2.67m/s，此前m向右减速，M向左减速，此后m将向左加速，M继续向左减速；当两者速度达到相同时，即速度均为2m/s时，两者相对静止，一起向左匀速直线运动。由此可知当M的速度为2.4m/s时，m处于向左加速过程中，A对。‎ ‎【答案】A ‎【拓展提升】本题实际上要求同学们能将滑块与滑板的运动过程全部弄清楚，才能知道板的速度为2.4ms时，两者的运动情况，通过两个动量守恒定律即可解决，要注意矢量性。如果问题是：当物块的速度大小为2.4m/s时物块的运动情况呢？‎ ‎【调研3】如图为某生产流水线工作原理示意图．足够长的工作平台上有一小孔A，一定长度的操作板（厚度可忽略不计）静止于小孔的左侧，某时刻开始，零件（可视为质点）无初速地放上操作板的中点，同时操作板在电动机带动下向右做匀加速直线运动，直至运动到A孔的右侧（忽略小孔对操作板运动的影响），最终零件运动到A孔时速度恰好为零，并由A孔下落进入下一道工序．已知零件与操作板间的动摩擦因数μ1=0.05，零件与与工作台间的动摩擦因数μ2=0.025，不计操作板与工作台间的摩擦．重力加速度g=‎10m/s2．求：‎ ‎（1）操作板做匀加速直线运动的加速度大小；‎ ‎（2）若操作板长L=‎2m，质量M=‎3kg，零件的质量m=‎0.5kg，则操作板从A孔左侧完全运动到右侧的过程中，电动机至少做多少功？‎ A 工作台 工作台 操作板 零件 ‎【解析】（1）设零件向右运动距离x时与操作板分离，此过程历经时间为t，此后零件在工作台上做匀减速运动直到A孔处速度减为零，设零件质量为m，操作板长为L，取水平向右为正方向，对零件，有：‎ 分离前：μ1mg＝ma1，分离后：μ2mg＝ma2，且x＝a1t2‎ 以后做匀减速运动的位移为：－x＝ 对操作板，有：＋x＝at2‎ 联立以上各式解得：a＝，代入数据得：a＝2m/s2‎ ‎（2）将a＝2m/s2，L＝2m代入＋a1t2＝at2，解得：t＝＝s 操作板从A孔左侧完全运动到右侧的过程中，动能的增加量△Ek1＝M()2=12J 零件在时间t内动能的增加量△Ek2＝m(μ1gt)2=J 零件在时间t内与操作板摩擦产生的内能Q1＝μ1mg×＝0.25J 根据能量守恒定律，电动机做功至少为W＝△Ek1＋△Ek2＋Q1＝12J≈12.33J ‎【方法点拔】本题的第一个难点在于为什么操作板具某一个加速度才有题目中所描述的情景出现？试想如果操作板的加速度很大，工件是不是冲过A孔，如果操作板的加速度很小，工件能到达A孔吗？第二个难点在于工件与操作板之间的两个关联，一个是相对位移为操作板的一半长度，另一个是工件在操作板上和操作平台上运动的位移之和等于操作板的一半长度，尽管操作板的长度未知，但这种位移关联和相互作用具有相同时间的关联是建立方程的重要依据。‎ ‎30°‎ A B ‎【调研4】如图所示，皮带传动装置与水平面夹角为30°，轮半径R= m，两轮轴心相距L=‎3.75m，A、B分别是传送带与两轮的切点，轮缘与传送带之间不打滑。一个质量为‎0.1kg的小物块与传送带间的动摩擦因数为μ= 。g取‎10m/s2。‎ ‎（1）当传送带沿逆时针方向以v1=‎3m/s的速度匀速运动时，将小物块无初速地放在A点后，它运动至B点需多长时间？（计算中可取≈16，≈20）‎ ‎（2）小物块相对于传送带运动时，会在传送带上留下痕迹。当传送带沿逆时针方向匀速运动时，小物块无初速地放在A点，运动至B点飞出。要想使小物块在传送带上留下的痕迹最长，传送带匀速运动的速度v2至少多大？‎ ‎【解析】（1）当小物块速度小于‎3m/s时，小物块受到竖直向下、垂直传送带向上的支持力和沿传送带斜向下的摩擦力作用，做匀加速直线运动，设加速度为a1，根据牛顿第二定律 mgsin30° + μmgcos30°=ma1，解得 a1 = ‎7.5m/s2‎ 当小物块速度等于‎3m/s时，设小物块对地位移为L1，用时为t1，根据匀加速直线运动规律 t1 = ，L1 = ，解得 t1 = 0.4s L1 = ‎‎0.6m 由于L1＜L 且μ＜tan30°，当小物块速度大于‎3m/s时，小物块将继续做匀加速直线运动至B点，设加速度为a2，用时为t2，根据牛顿第二定律和匀加速直线运动规律 mgsin30°－μmgcos30°=ma2，解得 a2 = ‎2.5m/s2‎ L－L1 = v1t2 + a2t22，解得 t2 = 0.8s 故小物块由禁止出发从A到B所用时间为 t = t1 + t2 = 1.2s ‎（2）通过作v—t图分析知：传送带匀速运动的速度越大，小物块从A点到B点用时越短，当传送带速度等于某一值v′ 时，小物块将从A点一直以加速度a1做匀加速直线运动到B点，所用时间最短，即 L = a1tmin2，解得tmin = 1s v′ =a1 tmin =7.5m/s，此时小物块和传送带之间的相对路程为 △S = v′ t－L = ‎‎3.75m 传送带的速度继续增大，小物块从A到B的时间保持不变，而小物块和传送带之间的相对路程继续增大，小物块在传送带上留下的痕迹也继续增大；当痕迹长度等于传送带周长时，痕迹为最长Smax，设此时传送带速度为v2，则Smax = ‎2L + 2πR，Smax = v2t－L ，联立解得 v2 = 12.25m/s ‎【学法指导】本题的第一问的受力分析与过程分析相信是非常熟悉的，但第二问中的最长划痕实际上受到传送带总长度的限制，最多只能等于传送带的总长度。而传送带的速度多大时才能使划痕正好等于传送带的总长度就是问题的关键了。‎ ‎【拓展训练】‎ ‎1、如图所示，子弹水平射入放在光滑水平地面上静止的木块，子弹未穿透木块，此过程产生的内能为6J，那么此过程木块动能可能增加了（ ）‎ A、12J B、16J C、4J D、6J ‎1、C【解析】系统产生的内能为f△S＝6J，对木块有动能定理可知fS木＝EK，其中△S为子弹打入的木块的深度，S木为木块运动的位移，子弹未穿出，画出子弹和木块运动的v－t图象，显然可看出△S＞S木，故EK＜6J，则根据选项可判断C正确。‎ ‎2、【2020年全国新课标卷第21题】‎ ‎2、A【解析】F力较小时，m1与m2相对静止，则F＝(m1＋m2)a，则a＝t，故a随时间t均匀增大。当F力较大时，两者相对运动，由于m2与m1之间的摩擦力为滑动摩擦力，根据滑动摩擦力与正压力成正比，可知该滑动摩擦力不变，m1的加速度不会改变，而m2的加速度随着F的增大而增大，且满足F－μm2g＝m2a2，a2＝t－μg，显然a2－t函数图线的斜率比a－t函数图线的斜率大，故A正确。‎ ‎3、如图所示，光滑水平面MN的左端M处由一弹射装置P（P为左端固定，处于压缩状态且锁定的轻质弹簧，当A与P碰撞时P立即解除锁定），右端N处与水平传送带恰平齐且很靠近，传送带沿逆时针方向以恒定速率v＝5m/s匀速转动，水平部分长度L＝4m。放在水平面上的两相同小物块A、B（均视为质点）间有一被压缩的轻质弹簧，弹性势能EP＝4J，弹簧与A相连接，与B不连接，A、B与传送带间的动摩擦因数μ＝0.2，物块质量mA＝mB＝1kg。现将A、B由静止开始释放，弹簧弹开，在B离开弹簧时，A未与P碰撞，B未滑上传送带。取g＝10m/s2。求：‎ ‎（1）B滑上传送带后，向右运动的最远处与N点间的距离sm ‎（2）B从滑上传送带到返回到N端的时间t和这一过程中B与传送带间因摩擦而产生的热能Q ‎（3）B回到水平面后压缩被弹射装置P弹回的A上的弹簧，B与弹簧分离然后再滑上传送带。则P锁定时具有的弹性势能E满足什么条件，才能使B与弹簧分离后不再与弹簧相碰。‎ A B P M N L v D ‎3、【解析】（1）弹簧弹开的过程中，系统机械能守恒Ep = mAυA2 + mBυB2‎ 由动量守恒有mAvA－mBvB＝0‎ 联立以上两式解得vA＝‎2m/s，vB＝‎2m/s B滑上传送带做匀减速运动，当速度减为零时，向右运动的距离最大。‎ 由动能定理得：－μmBgsm＝0 －mBvB 2，解得sm＝＝‎‎1m ‎（2）物块B先向右做匀减速运动，直到速度减小到零，然后反方向做匀加速运动，回到皮带左端时速度大小仍为vB＝‎2m/s 由动量定理：－μmBgt＝－mBvB－mBvB，解得t＝＝2s B向右匀减速运动因摩擦而产生的热能为：Q1＝μmBg(＋sm)‎ B向左匀加速运动因摩擦而产生的热能为：Q2＝μmBg(－sm)‎ Q＝Q1＋Q2＝μmBgvt＝20J ‎（3）设弹射装置P将A弹开时的速度为vA′，则E＝mAvA′2－mAvA2‎ B离开弹簧时，AB速度互换，B的速度vB′＝vA′‎ B与弹簧分离后不再与弹簧相碰，则B滑出平台Q端，由能量关系有mBvB′2＞μmB gL 以上三式解得E＞μmA gL－mAvA2，代入数据解得E＞6J ‎4、如图（a）所示，在足够长的光滑水平面上，放置一长为L＝‎1m、质量为m1＝‎0.5kg的木板A，一质量为m2＝‎1kg的小物体B以初速度v0滑上A的上表面的同时对A施加一个水平向右的力F，A与B之间的动摩擦因数为μ＝0.2，g＝‎10m/s2；小物体B在A上运动的路程S与F力的关系如图（b）所示。求：v0、F1、F2 。‎ B A v0‎ F ‎（a）‎ ‎（b）‎ F/N F2‎ F1‎ ‎1‎ S/m ‎1‎ O ‎4、【解析】（1）由图象可看出当F≤1N时，B物体在A板上的路程始终等于板长L，当F＝1N时，刚好不从A板右端掉下，此后A和B一起相对静止并加速运动。‎ 设B物体的加速度为a2，A板的加速度为a1，分别由牛顿第二定律：‎ μm‎2g＝m2a2 ，F＋μm‎2g＝m1a1‎ 设B运动的位移为S2，A运动的位移为S1，经过t时间两者速度均为v，根据运动学公式：‎ SB＝t ，SA＝t ，v＝v0－a2t＝a1t B在A上相对A向右运动的路程S＝SB－SA 联立解得：S＝ ，将F＝1N，S＝‎1m代入，解得：v0＝‎4m/s ‎（2）分析可知，当1N≤F≤F1时，随着F力增大，S减小，当F＝F1时，出现S突变，说明此时A、B在达到共同速度后，恰好再次发生相对运动，B将会从A板左端掉下。‎ 对A、B恰好发生相对运动时，B的加速度为a2，则整体加速度也为a2，由牛顿第二定律：‎ F1＝(m1＋m2)a2，解得F1＝3N ‎（3）此时B在A上运动的路程为S1＝＝m 当F≥F1时，物体B在A板上的路程为B相对A向右运动的路程的两倍。‎ 故当F＝F2时，将S＝0.5S1，解得：F2＝9N