- 2021-06-07 发布 |
- 37.5 KB |
- 2页

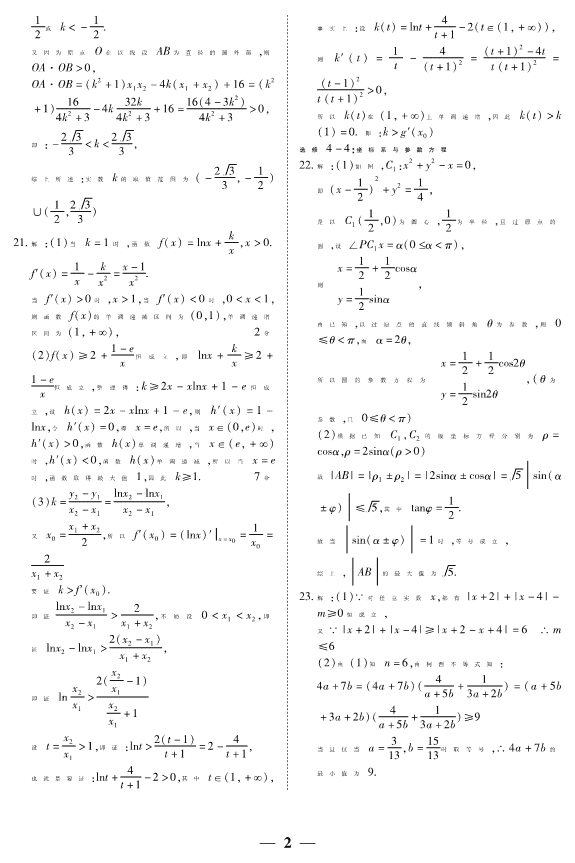
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
陕西省2019届高三第二次教学质量检测数学(文)答案
书书书 !"#$ 年高三第二次教学质量检测 文科数学答案!仅供参考" 一#选择题 #%&'!%(')%*'+%(',%*'-%&'.%/ 0%&'$%*'#"%('##%/'#!%/ #)!! 1,""#'#+!2$'#,!-'#-!!" #.!解!##连接 "#" 在!"$#中" 由余弦定理 得$ "#! 3"$! 4$#! 2!"$% $#567""$#3$" 8"#3)! 9"$3$# 8"$"#3"$#"3# - " 又"$#%3!# ) " 8""#%3# ! " 在 :;!"#%中""%3 "#! 4#%槡 ! 3,! !!#在!"&%中"""&%3!# ) " "%3,!"&%"3# + 由正弦定理得 "% 7<= !! ) 3 &" 7<= # + " 即$ , 槡) ! 3&" 槡! ! "得$"&3 槡, - ) 当"&%"3! + 时"赛道 "&的长度为 槡, - ) ! #0!解$!##由折线图可知统计数据!'"(#共有 - 组" 即!#"###"!!"#)#"!)"#-#"!+"#,#"!,"!"#" !-"!##" 计算可得 '3# 4! 4) 4+ 4, 4- - 3)!,"(3# - # - )3# ()3# - %$- 3#-" 所以 *>3 # + )3# !')2'#!()2(# # + )3# !')2'# ! 3 # + )3# ')()2+ '%( # + )3# !')2'# ! 3 ).# 2-%)!,%#- #.!, 3!" ,>3(>2*>'3#- 2!%)!, 3$" 所以月度利润 (与月份代码 '之间的线性回归 方程为 (>3!'4$! 当 '3## 时"(>3! ?## 4$ 3)#! 故预计甲公司 !"#$ 年 ) 月份的利润为 )# 百万 元! !!#&型新材料对应产品的使用寿命的平均数 为'# 3!!)," "型新材料对应的产品的使用寿 命的平均数为'! 3!!."9'# @'! 8应该采购 " 型新材料! #$!!##证明$连接 &-"在!&-&# 中"作 -.$&&# 于点 ." 因为 &&# //""# "得 -.$""# " 因为 &# -$平面 &"$" 所以 &# -$"$" 因为 &"3&$"-为 "$中点""得 &-$"$" 所以 "$$平面 &-&# " 所以 "$$-." 所以 -.$平面 ""# $# $" 又 &-3 &"! 2"-槡 ! 槡3 ,"&&# 3)"由 &-! 3&. %&&# "得$&.3, ) 第 #$ 题答图 !!# 由!## 可知 "$$ 平面 &-&# " 所以 "$$""# " 所 以 %"$$# "# 为 矩 形"故 0矩形"$$#"# 3#!& 联 结 &# "" &# " 3 &# -! 4-"槡 ! 3 ! 槡!" 在 "&"&# 中"&"3&&# 3)"&# " 槡3! ! 所以 0!&"&# 槡3 #+ 因为 0四边形&""&# 3!0!&"&# 槡3! #+ 所以 0侧 槡3+ #+ 4#! !"!解$!###由题可知 !! ,! 4)! *! 3# !,{ 30 "解得 ,! 3#- *!{ 3#!" 所以椭圆的标准方程为$ '! #- 4(! #! 3#! !!#设 &! '# "(# #""! '! "(! # 由 '! #- 4(! #! 3# (31'{ 2+ "得 !+1! 4)#'! 2)!1'4#- 3"" 由韦达定理得$'# 4'! 3 )!1 +1! 4)"'# '! 3 #- +1! 4)" 由 "A"&! 2)!1# ! 2+!+1! 4)#%#- A" 得 1 ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' A '!' # ! 或 1@2# ! ! 又因为原点 2在以线段 &"为直径的圆外部"则 2&%2"A"" 2&%2"3!1! 4##'# '! 2+1!'# 4'! # 4#- 3!1! 4## #- +1! 4) 2+1 )!1 +1! 4) 4#- 3#-!+ 2)1! # +1! 4) A"" 即$ 2 槡! ) ) @1@ 槡! ) ) " 综上所述$实数 1的取值范围为! 2 槡! ) ) " 2# ! # (! # ! " 槡! ) ) # !#!解$!##当 13# 时"函数 3!'# 3B='4 1 '"'A"! 34!'# 3# '21 '! 3'2# '! ! 当 34!'# A" 时"'A#"当 34!'# @" 时"" @'@#" 则函数 3!'#的单调递减区间为!""##"单调递增 区间为!#" 4!#" ! 分 !!#3!'# )! 4# 25 ' 恒成立"即 B='4 1 ')! 4 # 25 ' 恒成立"整理得$1)!'2'B='4# 25恒成 立"设 6!'# 3!'2'B='4# 25"则 64!'# 3# 2 B='"令 64!'# 3""得 '35"所以"当 '*!""5#时" 64!'# A""函数 6!'#单调递增"当 '*!5" 4!# 时"64!'# @""函数 6!'#单调递减"所以当 '35 时"函数取得最大值 #"因此 1)#! . 分 !)#13(! 2(# '! 2'# 3B='! 2B='# '! 2'# " 又 '" 3'# 4'! ! "所以 34!'" # 3!B='#4'3'" 3# '" 3 ! '# 4'! 要证 1A34!'" #! 即证B='! 2B='# '! 2'# A ! '# 4'! "不妨设 " @'# @'! "即 证 B='! 2B='# A!!'! 2'# # '# 4'! " 即证 B= '! '# A !! '! '# 2## '! '# 4# 设 73'! '# A#"即证$B=7A!!72## 74# 3! 2 + 74#" 也就是要证$B=74 + 74# 2! A""其中 7*!#" 4!#" 事实上$设 1!7# 3B=74 + 74# 2!!7*!#" 4!##" 则 14! 7# 3 # 7 2 + !74## ! 3!74## ! 2+7 7!74## ! 3 !72## ! 7!74## ! A"" 所以 1!7#在!#" 4!#上单调递增"因此 1!7# A1 !## 3"!即$1A84!'" # 选修 + 2+$坐标系与参数方程 !!!解$!##如图"$# $'! 4(! 2'3"" 即!'2# ! # ! 4(! 3# + " 是以 $# ! # ! ""#为圆心" # ! 为半径"且过原点的 圆"设"9$# '3#!" "#@!#" 则 '3# ! 4# ! 567# (3# ! 7<={ # " 由已知"以过原点的直线倾斜角 $为参数"则 " +$@!"而 #3!$" 所以圆的参数方程为 '3# ! 4# ! 567!$ (3# ! 7<=!{ $ "! $为 参数"且 "+$@!# !!#根据已知 $# "$! 的极坐标方程分别为 %3 567#"%3!7<=#!%A"# 故C&"C3C%# 1%! C3C!7<=#1567# 槡C3 , 7<=!# 1&# +槡,"其中 ;D=&3# ! ! 故当 7<=!#1&# 3# 时"等号成立" 综上" &" 的最大值为槡,! !)!解$!##9对任意实数 '"都有C'4! C4C'2+ C2 :)" 恒成立" 又9C'4! C4C'2+ C) C'4! 2'4+ C3-'8: +- !!#由!##知 + 3-"由柯西不等式知$ +, 4.*3!+, 4.*#! + , 4,*4 # ), 4!*# 3!, 4,* 4), 4!*#! + , 4,*4 # ), 4!*#)$ 当且仅当 , 3) #)"*3#, #) 时取等号"8+, 4.*的 最小值为 $ ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ! '"'查看更多