2021届浙江新高考数学一轮复习教师用书:第五章 3 第3讲 平面向量的数量积及应用举例
第3讲 平面向量的数量积及应用举例
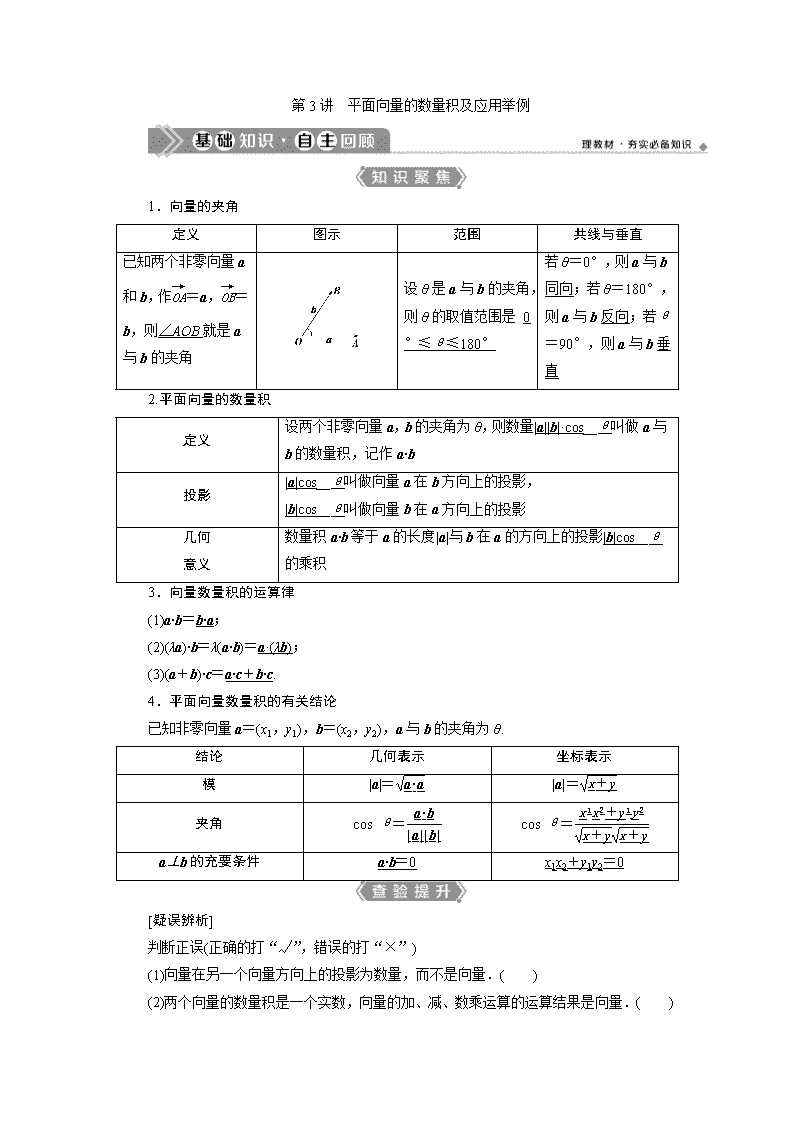
1.向量的夹角
定义
图示
范围
共线与垂直
已知两个非零向量a和b,作=a,=b,则∠AOB就是a与b的夹角
设θ是a与b的夹角,则θ的取值范围是 0°≤θ≤180°
若θ=0°,则a与b同向;若θ=180°,则a与b反向;若θ=90°,则a与b垂直
2.平面向量的数量积
定义
设两个非零向量a,b的夹角为θ,则数量|a||b|·cos__θ叫做a与b的数量积,记作a·b
投影
|a|cos__θ叫做向量a在b方向上的投影,
|b|cos__θ叫做向量b在a方向上的投影
几何
意义
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos__θ的乘积
3.向量数量积的运算律
(1)a·b=b·a;
(2)(λa)·b=λ(a·b)=a·(λb);
(3)(a+b)·c=a·c+b·c.
4.平面向量数量积的有关结论
已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
结论
几何表示
坐标表示
模
|a|=
|a|=
夹角
cos θ=
cos θ=
a⊥b的充要条件
a·b=0
x1x2+y1y2=0
[疑误辨析]
判断正误(正确的打“√”,错误的打“×”)
(1)向量在另一个向量方向上的投影为数量,而不是向量.( )
(2)两个向量的数量积是一个实数,向量的加、减、数乘运算的运算结果是向量.( )
(3)由a·b=0可得a=0或b=0.( )
(4)(a·b)c=a(b·c).( )
(5)两个向量的夹角的范围是.( )
(6)若a·b>0,则a和b的夹角为锐角;若a·b<0,则a和b的夹角为钝角.( )
答案:(1)√ (2)√ (3)× (4)× (5)× (6)×
[教材衍化]
1.(必修4P108A组T6改编)已知a·b=-12,|a|=4,a和b的夹角为135°,则|b|为( )
A.12 B.6 C.3 D.3
解析:选B.a·b=|a||b|cos 135°=-12,所以|b|==6.
2.(必修4P105例4改编)已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k=________.
解析:因为2a-b=(4,2)-(-1,k)=(5,2-k),由a·(2a-b)=0,得(2,1)·(5,2-k)=0,
所以10+2-k=0,解得k=12.
答案:12
3.(必修4P106练习T3改编)已知|a|=5,|b|=4,a与b的夹角θ=120°,则向量b在向量a方向上的投影为________.
解析:由数量积的定义知,b在a方向上的投影为|b|cos θ=4×cos 120°=-2.
答案:-2
[易错纠偏]
(1)没有找准向量的夹角致误;
(2)不理解向量的数量积的几何意义致误;
(3)向量的数量积的有关性质应用不熟练致误.
1.已知△ABC的三边长均为1,且=c,=a,=b,则a·b+b·c+a·c=________.
解析:因为a,b=b,c=a,c=120°,|a|=|b|=|c|=1,所以a·b=b·c=a·c=1×1×cos 120°=-,所以a·b+b·c+a·c=-.
答案:-
2.已知点A(-1,1),B(1,2),C(-2,-1),D(3,4),则向量在
方向上的投影为________.
解析:=(2,1),=(5,5),由定义知,在方向上的投影为==.
答案:
3.设向量a=(-1,2),b=(m,1),如果向量a+2b与2a-b平行,那么a与b的数量积等于________.
解析:a+2b=(-1+2m,4),2a-b=(-2-m,3),由题意得3(-1+2m)-4(-2-m)=0,则m=-,所以a·b=-1×+2×1=.
答案:
平面向量数量积的运算
(1)如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O.记I1=·,I2=·,I3=·,则( )
A.I1<I2<I3
B.I1<I3<I2
C.I3 < I1<I2
D.I2<I1<I3
(2)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则·(+)的最小值是( )
A.-2 B.-
C.- D.-1
【解析】 (1)如图所示,四边形ABCE是正方形,F为正方形的对角线的交点,易得AO
I3,作AG⊥BD于G,又AB=AD,所以OB·,即I1>I3.所以I30)上,如图,数形结合可知|a-b|min=||-||=-1.故选A.
法二:由b2-4e·b+3=0得b2-4e·b+3e2=(b-e)·(b-3e)=0.
设b=,e=,3e=,所以b-e=,b-3e=,所以·=0,取EF的中点为C,则B在以C为圆心,EF为直径的圆上,如图.设a=,作射线OA,使得∠AOE=,所以|a-b|=|(a-2e)+(2e-b)|≥|a-2e|-|2e-b|=||-||≥-1.故选A.
【答案】 A
角度三 两向量垂直问题
已知|a|=4,|b|=8,a与b的夹角是120°.求k为何值时,(a+2b)⊥(ka-b)?
【解】 由已知得,a·b=4×8×=-16.
因为(a+2b)⊥(ka-b),
所以(a+2b)·(ka-b)=0,
ka2+(2k-1)a·b-2b2=0,
即16k-16(2k-1)-2×64=0.
所以k=-7.
即k=-7时,a+2b与ka-b垂直.
角度四 求参数值或范围
已知△ABC是正三角形,若-λ与向量的夹角大于90°,则实数λ的取值范围是________.
【解析】 因为-λ与向量的夹角大于90°,所以(-λ)·<0,即||2-λ||·||cos 60°<0,解得λ>2.故填(2,+∞).
【答案】 (2,+∞)
(1)求平面向量的夹角的方法
①定义法:利用向量数量积的定义知,cos θ=,其中两个向量的夹角θ的范围为[0,π],求解时应求出三个量:a·b,|a|,|b|或者找出这三个量之间的关系;
②坐标法:若a=(x1,y1),b=(x2,y2),则cos θ=;
(2)求向量的模的方法
①公式法:利用|a|=及(a±b)2=|a|2±2a·b+|b|2,把向量模的运算转化为数量积运算.
②几何法:利用向量的几何意义,即利用向量加、减法的平行四边形法则或三角形法则作出向量,再利用余弦定理等方法求解.
1.(2020·浙江新高考研究联盟)已知向量a,b,c满足|a|=1,|b|=k,|c|=2-k且a+b+c=0,则b与c夹角的余弦值的取值范围是________.
解析:设b与c的夹角为θ,由题b+c=-a,
所以b2+c2+2b·c=1.
即cos θ==1+.
因为|a|=|b+c|≥|b-c|,所以|2k-2|≤1.
所以≤k≤.
所以-1≤cos θ≤-.
答案:
2.已知向量与的夹角为120°,且||=3,||=2.若=λ+,且⊥,则实数λ的值为________.
解析:因为⊥,所以·=0.
又=λ+,=-,
所以(λ+)·(-)=0,
即(λ-1)·-λ2+2=0,
所以(λ-1)||||cos 120°-9λ+4=0.
所以(λ-1)×3×2×(-)-9λ+4=0.解得λ=.
答案:
向量数量积的综合应用
(2020·金华十校联考)在△ABC中,角A,B,C的对边分别为a,b,c,向量m=
(cos(A-B),sin(A-B)),n=(cos B,-sin B),且m·n=-.
(1)求sin A的值;
(2)若a=4,b=5,求角B的大小及向量在方向上的投影.
【解】 (1)由m·n=-,
得cos(A-B)cos B-sin(A-B)sin B=-,
所以cos A=-.
因为0b,所以A>B,则B=,由余弦定理得=52+c2-2×5c×,解得c=1.
故向量在方向上的投影为
||cos B=ccos B=1×=.
平面向量与三角函数的综合问题
(1)题目条件给出的向量坐标中含有三角函数的形式,运用向量共线或垂直或等式成立等,得到三角函数的关系式,然后求解.
(2)给出用三角函数表示的向量坐标,要求的是向量的模或者其他向量的表达形式,解题思路是经过向量的运算,利用三角函数在定义域内的有界性,求得值域等.
1.在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量m=,n=,且2m·n+|m|=,则∠A=________.
解析:因为2m·n=2sin cos -2cos2 =sin A-(cos A+1)=sin -1,
又|m|=1,
所以2m·n+|m|=sin=,
即sin=.
因为00,b>0)的左焦点,定点A为双曲线虚轴的一个端点,过F,A两点的直线与双曲线的一条渐近线在y轴右侧的交点为B,若=3,则此双曲线的离心率为________.
【解析】 (1)由椭圆+=1可得F(-1,0),点O(0,0),设P(x,y)(-2≤x≤2),
则·=x2+x+y2=x2+x+3
=x2+x+3=(x+2)2+2,-2≤x≤2,
当且仅当x=2时,·取得最大值6.
(2)由F(-c,0),A(0,b),得直线AF的方程为y=x+b.
根据题意知,直线AF与渐近线y=x相交,
联立得消去x得,yB=.
由=3,得yB=4b,所以=4b,化简得3c=4a,
所以离心率e=.
【答案】 (1)6 (2)
向量在解析几何中的2个作用
载体
作用
向量在解析几何问题中出现,多用于“包装”,解决此类问题的关键是利用向量的意义、运算脱去“向量外衣”,导出曲线上点的坐标之间的关系,从而解决有关距离、斜率、夹角、轨迹、最值等问题
工具
作用
利用a⊥b⇔a·b=0(a,b为非零向量),a∥b⇔a=λb(b≠0)可解决垂直、平行问题,特别地,向量垂直、平行的坐标表示对于解决解析几何中的垂直、平行问题是一种比较简捷的方法
[基础题组练]
1.已知A,B,C为平面上不共线的三点,若向量=(1,1),n=(1,-1),且n·=2,则n·等于( )
A.-2 B.2
C.0 D.2或-2
解析:选B.n·=n·(+)=n·+n·=(1,-1)·(-1,-1)+2=0+2=2.
2.(2020·温州市十校联合体期初)设正方形ABCD的边长为1,则|-+|等于( )
A.0 B.
C.2 D.2
解析:选C.正方形ABCD的边长为1,则|-+|2=|+|2=||2+||2+2·=12+12+12+12=4,所以|-+|=2,故选C.
3.(2020·温州市十校联合体期初)已知平面向量a,b,c满足c=xa+yb(x,y∈R),且a·c>0,b·c>0.( )
A.若a·b<0则x>0,y>0
B.若a·b<0则x<0,y<0
C.若a·b>0则x<0,y<0
D.若a·b>0则x>0,y>0
解析:选A.由a·c>0,b·c>0,若a·b<0,
可举a=(1,1),b=(-2,1),c=(0,1),
则a·c=1>0,b·c=1>0,a·b=-1<0,
由c=xa+yb,即有0=x-2y,1=x+y,
解得x=,y=,则可排除B;
若a·b>0,可举a=(1,0),b=(2,1),c=(1,1),
则a·c=1>0,b·c=3>0,a·b=2>0,
由c=xa+yb,即有1=x+2y,1=y,解得x=-1,y=1,
则可排除C,D.故选A.
4.在△ABC中,(+)·=||2,则△ABC的形状一定是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
解析:选C.由(+)·=||2,得·(+-)=0,即·(++)=0,
所以2·=0,所以⊥.
所以∠A=90°,又因为根据条件不能得到||=||.故选C.
5.已知正方形ABCD的边长为2,点F是AB的中点,点E是对角线AC上的动点,则·的最大值为( )
A.1 B.2
C.3 D.4
解析:选B.以A为坐标原点,,方向分别为x轴、y轴的正方向建立平面直角坐标系(图略),则F(1,0),C(2,2),D(0,2),设E(λ,λ)(0≤λ≤2),则=(λ,λ-2),=(1,2),所以·=3λ-4≤2.
所以·的最大值为2.故选B.
6.(2020·金华市东阳二中高三月考)若a,b是两个非零向量,且|a|=|b|=λ|a+b|,λ∈,则b与a-b的夹角的取值范围是( )
A. B.
C. D.
解析:选B.因为|a|=|b|=λ|a+b|,λ∈,
不妨设|a+b|=1,则|a|=|b|=λ.
令=a,=b,以OA,OB为邻边作平行四边形OACB,
则平行四边形OACB为菱形.
故有△OAB为等腰三角形,故有∠OAB=∠OBA=θ,
且0<θ<.
而由题意可得,b与a-b的夹角,
即与的夹角,等于π-θ,
△OAC中,由余弦定理可得|OC|2=1=|OA|2+|AC|2-2|OA|·|AC|·cos 2θ=λ2+λ2-2·λ·λcos 2θ,
解得cos 2θ=1-.
再由≤λ≤1,可得≤≤,所以-≤cos 2θ≤,所以≤2θ≤,所以≤θ≤,
故≤π-θ≤,即b与a-b的夹角π-θ的取值范围是.
7.(2020·温州市十校联合体期初)已知平面向量a与b的夹角为120°,且|a|=|b|=4,那么|a-2b|=________.
解析:因为平面向量a与b的夹角为120°,且|a|=|b|=4,所以a·b=4·4·cos 120°=-8,
所以|a-2b|=====4.
答案:4
8.(2020·嘉兴一中高考适应性考试)设e1,e2为单位向量,其中a=2e1+e2,b=e2,且a在b上的投影为2,则a·b=________,e1与e2的夹角为________.
解析:设e1,e2的夹角为θ,因为a在b上的投影为2,
所以==2e1·e2+|e2|2=2|e1|·|e2|cos θ+1=2,解得cos θ=,则θ=.
a·b=(2e1+e2)·e2
=2e1·e2+|e2|2=2|e1|·|e2|cos θ+1=2.
答案:2
9.如图,在边长为2的正方形ABCD中,点Q为边CD上一个动点,=λ,点P为线段BQ (含端点)上一个动点.若λ=1,则·的取值范围为________.
解析:当λ=1时,Q为CD的中点.
设=m,=n,=μ(0≤μ≤1).
易知=-m+n,=+=m+μ=m+μn,
=-=m+μn-n=m+(μ-1)n,
所以·=·=·=4+4μ(μ-1)=5μ2-8μ+4.
根据二次函数性质可知,当μ=时上式取得最小值;当μ=0时上式取得最大值4.所以·的取值范围为.
答案:
10.(2020·温州市十五校联合体联考)已知坐标平面上的凸四边形ABCD满足=(1,),=(-,1),则凸四边形ABCD的面积为________;·
的取值范围是________.
解析:由=(1,),=(-,1)得⊥,且||=2,||=2,所以凸四边形ABCD的面积为×2×2=2;因为ABCD为凸四边形,所以AC与BD交于四边形内一点,记为M,则·=(-)·(-)=·+·-·-·,
设=λ,=μ,则λ,μ∈(0,1),且=-λ,=(1-λ),
=-μ,=(1-μ),所以·=-4μ(1-μ)-4λ(1-λ)∈[-2,0),所以有λ=μ=时,·取到最小值-2.
答案:2 [-2,0)
11.已知m=,n=(cos x,1).
(1)若m∥n,求tan x的值;
(2)若函数f(x)=m·n,x∈[0,π],求f(x)的单调递增区间.
解:(1)由m∥n得,sin-cos x=0,
展开变形可得,sin x=cos x,
即tan x=.
(2)f(x)=m·n=sin+,
由-+2kπ≤2x-≤+2kπ,k∈Z得,-+kπ≤x≤+kπ,k∈Z.
又x∈[0,π],所以当x∈[0,π]时,
f(x)的单调递增区间为和.
12.(2020·金华市东阳二中高三月考)设O是△ABC的三边中垂线的交点,a,b,c分别为角A,B,C对应的边,已知b2-2b+c2=0,求·的取值范围.
解:因为O是△ABC的三边中垂线的交点,故O是三角形外接圆的圆心,
如图所示,延长AO交外接圆于点D.
因为AD是⊙O的直径,所以∠ACD=∠ABD=90°.
所以cos∠CAD=,cos∠BAD=.
所以·=·(-)
=·-·
=||||·cos∠CAD-||||·cos∠BAD=||2-||2
=b2-c2
=b2-(2b-b2)(因为c2=2b-b2)
=b2-b=-.
因为c2=2b-b2>0,解得0
查看更多