2017-2018学年贵州省安顺市平坝第一高级中学高二9月月考数学（文）试题 缺答案

2017-2018学年贵州省安顺市平坝第一高级中学高二9月月考数学（文）试题 缺答案

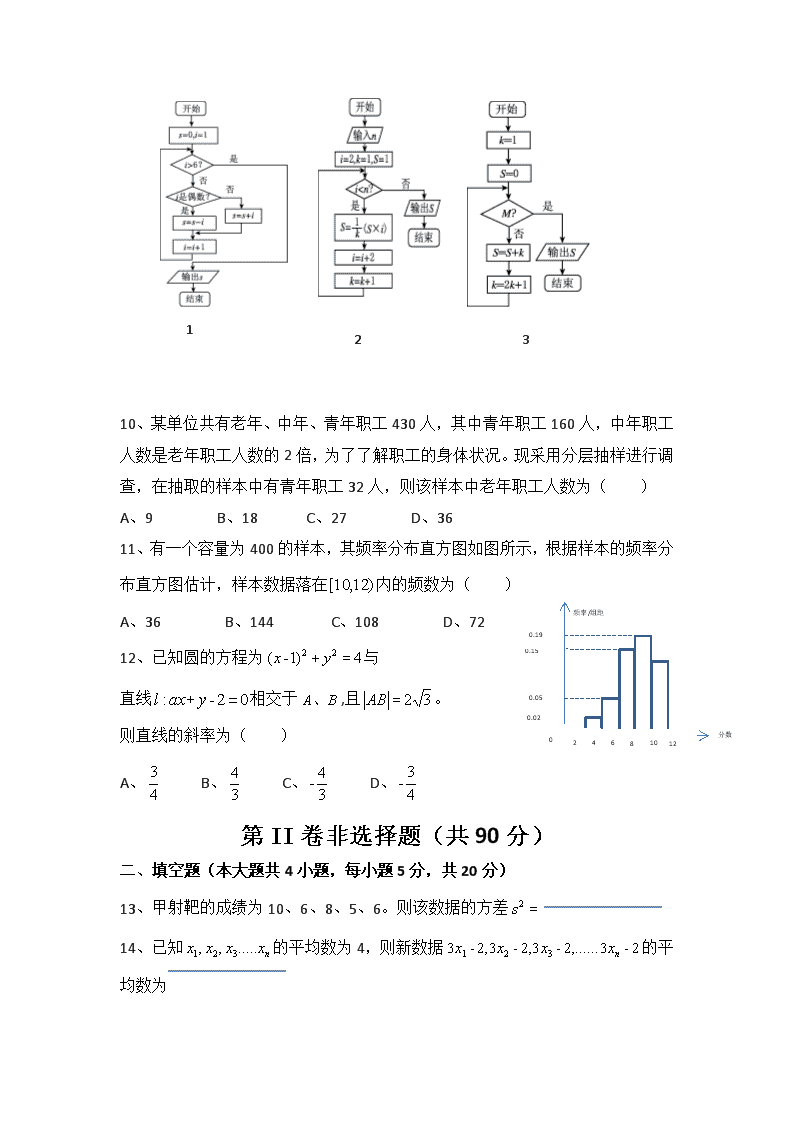
平坝第一高级中学2017-2018学年度第一学期 高二数学月考试卷（文科）（9月） ‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。‎ 第I卷（选择题，共60分）‎ 一、 选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中评，只有一项是符合要求的请将所选答案写在答题卡上）‎ 1、 为了欢庆国庆佳节，平坝区要从城关镇、夏云镇、乐平镇、白云镇、十字乡、齐伯乡抽取n个人参加文艺汇演。你认为最科学合理的抽样方法是（ ）‎ A、 抓阄法 B、分层抽样 C、系统抽样 D、随机数法 2、 化为十进制为（ ）‎ A、44 B、‎40 C、29 D、45‎ ‎7‎ ‎8‎ ‎9‎ 甲 ‎5‎ ‎0‎ ‎2‎ ‎2‎ ‎4‎ ‎8‎ 3、 已知圆的方程为，则圆心和半径为（ ）‎ A、 ‎ B、 C、 D、‎ 4、 如图，茎叶图是描述甲的8次数学成绩，由于不慎污损，‎ 5、 看不请相关数字。则甲的数学成绩的中位数是（ ）‎ A、81 B、‎82 C、83 D、84‎ 5、 用秦九韶算法求经过加法和乘法各几次 A、5、5 B、5、‎6 C、6、5 D、6、6‎ 6、 现有产品503个，用系统抽样抽取容量为50的样本。已知抽取第5个样本的编号为58号，则第3个样本的编号为（ ）‎ A、18 B、‎15 C、28 D、25‎ 7、 执行如图1所示的程序框图，则输出的s的值是(　　)‎ A．3 B．－‎3 C．－4 D．4‎ ‎8、执行如图2所示的程序框图，若输出的值S＝16，则输入自然数n的最小值应等于(　　)‎ A．7 B．‎8 C．9 D．10　　‎ 9、 ‎．执行如图3所示的程序框图，若输出的结果为11，则M处可填入的条件为(　　)‎ A．k≥31 B．k≥‎15C．k>31 D．k>15 ‎ ‎3‎ ‎2‎ ‎1‎ ‎ ‎ 10、 某单位共有老年、中年、青年职工430人，其中青年职工160人，中年职工人数是老年职工人数的2倍，为了了解职工的身体状况。现采用分层抽样进行调查，在抽取的样本中有青年职工32人，则该样本中老年职工人数为（ ）‎ A、9 B、‎18 C、27 D、36‎ 频率/组距 分数 ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎0‎ ‎10‎ ‎12‎ ‎0.02‎ ‎0.05‎ ‎0.15‎ ‎0.19‎ 11、 有一个容量为400的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在内的频数为（ ）‎ A、36 B、‎144 C、108 D、72‎ 12、 已知圆的方程为与 直线相交于,且。‎ 则直线的斜率为（ ）‎ A、 B、 C、 D、‎ 第II卷非选择题（共90分）‎ 一、 填空题（本大题共4小题，每小题5分，共20分）‎ ‎13、甲射靶的成绩为10、6、8、5、6。则该数据的方差 ‎14、已知的平均数为4，则新数据的平均数为 15、 已知之间的一组数据如下：‎ x ‎1‎ ‎3‎ ‎6‎ ‎7‎ ‎8‎ y ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 其中利用最小二乘法得到回归直线方程在y轴上的截距为2，则回归方程为 ‎16、已知等差数列中，，是的等比中项。则等差数列中前5项的平均数为 一、 解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）‎ 17、 ‎（10分）求98与77的最大公约数。（方法：更相减损术或辗转相除法）‎ ‎18、（12分）国庆佳节之际，平坝福乐多超市推行优惠措施。若购物金额x在800元以上（包括800元），则打8折。若购物金额x在800元以下500元以上（包括500元），则打9折。否则不打折。‎ ‎（1）写出消费金额y与购物金额x的关系。‎ ‎（2）画出对应的程序框图，要求输入购物金额x，输出消费金额y。‎ 19、 ‎（12分）甲、乙两位同学5次数学竞赛成绩如下：‎ 次数 第一次 第二次 第三次 第四次 第五次 甲 ‎87‎ ‎91‎ ‎90‎ ‎89‎ ‎93‎ 乙 ‎89‎ ‎90‎ ‎91‎ ‎88‎ ‎92‎ （1） 用茎叶图表示甲、乙的数学成绩。‎ （2） 甲、乙中要选一个去参加全国数学竞赛，你认为谁最适合去参加竞赛，请说明理由。‎ 20、 ‎（12分）某工厂的产品销售如下表：‎ 年份 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 时间代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 销量y（千万）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ （1） 求y关于t的回归直线方程。‎ （2） 用所求的回归直线方程预测该工厂在2018年（t=6）的销量。‎ 21、 从高二年级随机抽取40名学生。如图，得到他们期中数学成绩的频率分布直方图。‎ （1） 求图中实数的值。‎ （2） 若该校高二年级共有1000名学生，是估计该校高二年级学生期中考试数学成绩不低于60分的人数。‎ （3） 由图求出这40名高二年级学生期中成绩的中位数、平均成绩。‎ 频率/组距 分数 ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎0‎ ‎80‎ ‎90‎ ‎100‎ ‎0.005‎ a ‎0.02‎ ‎0.025‎ ‎0.03‎ 22、 已知圆圆心为，且圆经过点。直线。‎ （1） 求出圆的标准方程。‎ （2） 求圆上的点到直线的最大距离和最小距离。‎