2012高考试题分类汇编：导数

2012高考试题分类汇编：导数

‎2012高考试题分类汇编：导数 一、选择题 ‎1、【2012高考浙江文10】设a＞0，b＞0，e是自然对数的底数 A. 若ea+‎2a=eb+3b，则a＞b B. 若ea+‎2a=eb+3b，则a＜b C. 若ea‎-2a=eb-3b，则a＞b D. 若ea‎-2a=eb-3b，则a＜b ‎2、【2012高考陕西文9】设函数f（x）=+lnx 则 （ ）‎ A．x=为f(x)的极大值点 B．x=为f(x)的极小值点 C．x=2为 f(x)的极大值点 D．x=2为 f(x)的极小值点 ‎3、【2012高考辽宁文8】函数y=x2㏑x的单调递减区间为 ‎（A）（1,1] （B）（0,1] （C.）[1，+∞） （D）（0，+∞）‎ ‎4、【2102高考福建文12】已知f（x）=x³-6x²+9x-abc，a＜b＜c，且f（a）=f（b）=f（c）=0.现给出如下结论：‎ ‎ ①f（0）f（1）＞0；②f（0）f（1）＜0；③f（0）f（3）＞0；④f（0）f（3）＜0.‎ 其中正确结论的序号是 ‎ A.①③ B.①④ C.②③ D.②④‎ ‎5、【2012高考辽宁文12】已知P,Q为抛物线x2=2y上两点，点P,Q的横坐标分别为4，2，过P,Q分别作抛物线的切线，两切线交于点A，则点A的纵坐标为 ‎(A) 1 (B) 3 (C) 4 (D) 8‎ ‎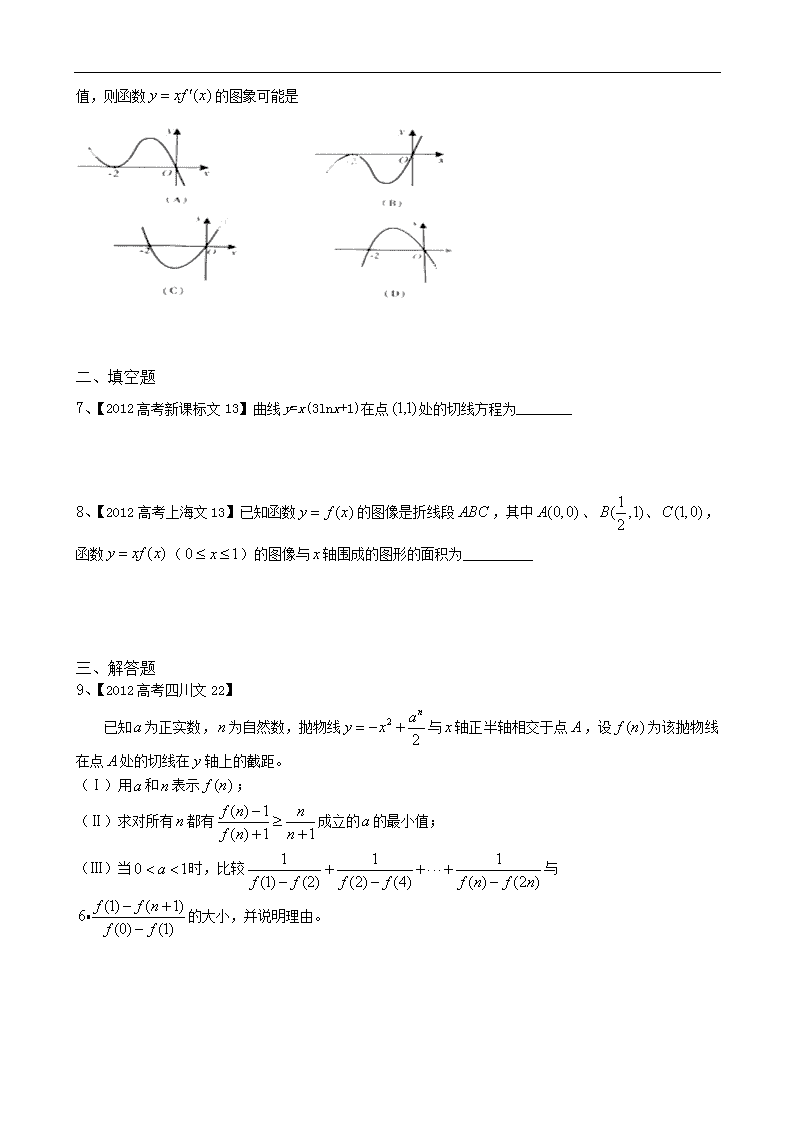6、【2012高考重庆文8】设函数在上可导，其导函数，且函数在 处取得极小值，则函数的图象可能是 ‎ ‎ 二、填空题 ‎7、【2012高考新课标文13】曲线y=x(3lnx+1)在点处的切线方程为________‎ ‎ ‎ ‎8、【2012高考上海文13】已知函数的图像是折线段，其中、、，函数（）的图像与轴围成的图形的面积为 ‎ 三、解答题 ‎9、【2012高考四川文22】‎ 已知为正实数，为自然数，抛物线与轴正半轴相交于点，设为该抛物线在点处的切线在轴上的截距。‎ ‎（Ⅰ）用和表示；‎ ‎（Ⅱ）求对所有都有成立的的最小值；‎ ‎（Ⅲ）当时，比较与 的大小，并说明理由。‎ ‎10、【2102高考北京文18】‎ 已知函数f(x)=ax2+1(a>0),g(x)=x3+bx。‎ 若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线，求a,b的值；‎ 当a=3,b=-9时，若函数f(x)+g(x)在区间[k,2]上的最大值为28，求k的取值范围。‎ ‎11、【2012高考江苏18】若函数在处取得极大值或极小值，则称为函数的极值点。‎ 已知是实数，1和是函数的两个极值点．‎ ‎（1）求和的值；‎ ‎（2）设函数的导函数，求的极值点；‎ ‎（3）设，其中，求函数的零点个数．‎ ‎12、【2012高考天津文科20】‎ 已知函数，x其中a>0.‎ ‎（I）求函数的单调区间；‎ ‎（II）若函数在区间（-2，0）内恰有两个零点，求a的取值范围；‎ ‎（III）当a=1时，设函数在区间上的最大值为M（t），最小值为m（t）,记g(t)=M(t)-m(t),求函数g(t)在区间上的最小值。‎ ‎13、【2102高考福建文22】‎ 已知函数且在上的最大值为，‎ ‎（1）求函数f(x)的解析式；‎ ‎(2)判断函数f(x)在（0，π）内的零点个数，并加以证明。‎ ‎ ‎ ‎14、【2012高考陕西文21】 ‎ 设函数 ‎（1）设，，证明：在区间内存在唯一的零点；‎ ‎（2）设n为偶数，，，求b+‎3c的最小值和最大值；‎ ‎（3）设，若对任意，有，求的取值范围；‎ ‎15、【2012高考湖南文22】‎ 已知函数f(x)=ex-ax，其中a＞0.[@#中国^教育出版&网~]‎ ‎（1）若对一切x∈R，f(x) 1恒成立，求a的取值集合；[z ‎（2)在函数f(x)的图像上去定点A（x1, f(x1)）,B(x2, f(x2))(x10时，(x－k) f´(x)+x+1>0，求k的最大值 ‎17、【2012高考重庆文17】已知函数在处取得极值为 ‎（1）求a、b的值；（2）若有极大值28，求在上的最大值． ‎ ‎18、【2012高考湖北文22】‎ 设函数，n为正整数，a,b为常数，曲线y=f(x)在（1，f(1)）处的切线方程为x+y=1.‎ ‎（1）求a,b的值；‎ ‎（2）求函数f(x)的最大值 ‎（3）证明：f(x)< .‎ ‎19、【2012高考安徽文17】‎ 设定义在（0，+）上的函数 ‎（Ⅰ）求的最小值；‎ ‎（Ⅱ）若曲线在点处的切线方程为，求的值。‎ ‎20、【2012高考江西文21】‎ 已知函数f(x)=（ax2+bx+c）ex在上单调递减且满足f(0)=1，f(1)=0.‎ ‎（1）求a的取值范围；‎ ‎（2）设g(x)= f(-x)- f′(x)，求g(x)在上的最大值和最小值。‎ ‎ ‎ ‎21、【2012高考辽宁文21】‎ 设，证明：‎ ‎ (Ⅰ)当x﹥1时， ﹤ （ ）‎ ‎ (Ⅱ)当时，‎ ‎22、【2012高考浙江文21】已知a∈R，函数 ‎（1）求f(x)的单调区间 ‎（2）证明：当0≤x≤1时，f(x)+ ＞0.‎ ‎23、【2012高考全国文21】‎ 已知函数 ‎（Ⅰ）讨论的单调性；‎ ‎（Ⅱ）设有两个极值点，若过两点，的直线与轴的交点在曲线上，求的值。‎ ‎ ‎ ‎24、【2012高考山东文22】 ‎ 已知函数为常数，e=2.71828…是自然对数的底数)，曲线在点处的切线与x轴平行.‎ ‎(Ⅰ)求k的值；‎ ‎(Ⅱ)求的单调区间；‎ ‎(Ⅲ)设，其中为的导函数.证明：对任意.‎ ‎25、【2012高考广东文21】‎ 设，集合，，.‎ ‎（1）求集合（用区间表示）‎ ‎（2）求函数在内的极值点.‎ 以下是答案 一、选择题 ‎1、 A ‎2、 D ‎3、 B ‎4、 C ‎5、 C ‎6、 C 二、填空题 ‎7、 ‎ ‎8、 。‎ 三、解答题 ‎9、 ‎ ‎10、 ‎ ‎11、 解：（1）由，得。‎ ‎ ∵1和是函数的两个极值点，‎ ‎ ∴ ，，解得。‎ ‎ （2）∵ 由（1）得， ，‎ ‎ ∴，解得。‎ ‎ ∵当时，；当时，，‎ ‎ ∴是的极值点。‎ ‎ ∵当或时，，∴ 不是的极值点。‎ ‎ ∴的极值点是－2。‎ ‎（3）令，则。‎ ‎ 先讨论关于 的方程 根的情况：‎ 当时，由（2 ）可知，的两个不同的根为I 和一2 ，注意到是奇函数，∴的两个不同的根为一和2。‎ 当时，∵， ，‎ ‎∴一2 , －1，1 ，2 都不是的根。‎ 由（1）知。‎ ‎① 当时， ，于是是单调增函数，从而。‎ 此时在无实根。‎ ‎② 当时．，于是是单调增函数。‎ 又∵，，的图象不间断，‎ ‎∴ 在（1 , 2 ）内有唯一实根。‎ 同理，在（一2 ，一I ）内有唯一实根。‎ ‎③ 当时，，于是是单调减两数。‎ 又∵， ，的图象不间断，‎ ‎∴在（一1，1 ）内有唯一实根。‎ 因此，当时，有两个不同的根满足；当 时 有三个不同的根，满足。‎ 现考虑函数的零点：‎ ‎( i ）当时，有两个根，满足。‎ 而有三个不同的根，有两个不同的根，故有5 个零点。‎ ‎( 11 ）当时，有三个不同的根，满足。‎ 而有三个不同的根，故有9 个零点。‎ 综上所述，当时，函数有5 个零点；当时，函数有9 个零点。‎ ‎【考点】函数的概念和性质，导数的应用。‎ ‎【解析】（1）求出的导数，根据1和是函数的两个极值点代入列方程组求解即可。‎ ‎ （2）由（1）得，，求出，令，求解讨论即可。‎ ‎ （3）比较复杂，先分和讨论关于 的方程 根的情况；再考虑函数的零点。‎ ‎12、 ‎ ‎13、 ‎ ‎14、 ‎ ‎15、 解：令.‎ 当时单调递减；当时单调递增，故当时，取最小值 于是对一切恒成立，当且仅当 ‎　　　　　.　　　　　　　　　　　　　　　　　　①‎ 令则 当时，单调递增；当时，单调递减.‎ 故当时，取最大值.因此，当且仅当时，①式成立.‎ 综上所述，的取值集合为.‎ ‎（Ⅱ）由题意知，‎ 令则 令，则.‎ 当时，单调递减；当时，单调递增.‎ 故当，即 从而，又 所以 因为函数在区间上的图像是连续不断的一条曲线，所以存在 使即成立.‎ ‎【解析】‎ ‎【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出取最小值对一切x∈R，f(x) 1恒成立转化为从而得出求a的取值集合；第二问在假设存在的情况下进行推理，然后把问题归结为一个方程是否存在解的问题，通过构造函数，研究这个函数的性质进行分析判断.‎ ‎16、‎ ‎17、 【解析】（Ⅰ）因 故 由于 在点 处取得极值 故有即 ，化简得解得 ‎（Ⅱ）由（Ⅰ）知 ，‎ 令 ，得当时，故在上为增函数；‎ 当 时， 故在 上为减函数 当 时 ，故在 上为增函数。‎ 由此可知 在 处取得极大值， 在 处取得极小值由题设条件知 得此时，因此 上的最小值为 ‎18、 ‎ ‎19、 【解析】（I）（方法一），‎ 当且仅当时，的最小值为。‎ ‎（II）由题意得：， ①‎ ‎， ②‎ 由①②得：。‎ ‎20、 ‎ ‎21、 ‎ ‎22、 【解析】（1）由题意得，‎ 当时，恒成立，此时的单调递增区间为.‎ 当时，，此时函数的单调递增区间为.‎ ‎(2)由于，当时，.‎ 当时，.‎ 设，则.‎ 则有 ‎0‎ ‎1‎ ‎-‎ ‎0‎ ‎+‎ ‎1‎ 减 极小值 增 ‎1‎ 所以.‎ 当时，.‎ 故.‎ ‎23、‎ ‎24、 (I)，‎ 由已知，，∴.‎ ‎(II)由(I)知，.‎ 设，则，即在上是减函数，‎ 由知，当时，从而，‎ 当时，从而.‎ 综上可知，的单调递增区间是，单调递减区间是.‎ ‎(III)由(II)可知，当时，≤0＜1+，故只需证明在时成立.‎ 当时，＞1，且，∴.‎ 设，，则，‎ 当时，，当时，，‎ 所以当时，取得最大值.‎ 所以.‎ 综上，对任意，.‎ ‎25、【解析】（1）令，‎ ‎。‎ ‎① 当时，，‎ 方程的两个根分别为，，‎ 所以的解集为。‎ 因为，所以。‎ ‎② 当时，，则恒成立，所以，‎ 综上所述，当时，；‎ 当时，。‎ ‎（2），‎ ‎ 令，得或。‎ ‎① 当时，由（1）知，‎ 因为，，‎ 所以，‎ 所以随的变化情况如下表：‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ ‎↗‎ 所以的极大值点为，没有极小值点。‎ ‎② 当时，由（1）知，‎ 所以随的变化情况如下表：‎ ‎0‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ 极小值 ‎↗‎ 所以的极大值点为，极小值点为。‎ 综上所述，当时，有一个极大值点，没有极小值点；‎ 当时，有一个极大值点，一个极小值点。‎