- 2021-06-07 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017届高考文科数学(全国通用)二轮文档讲义:第2编专题2-3-1三角函数的图象与性质
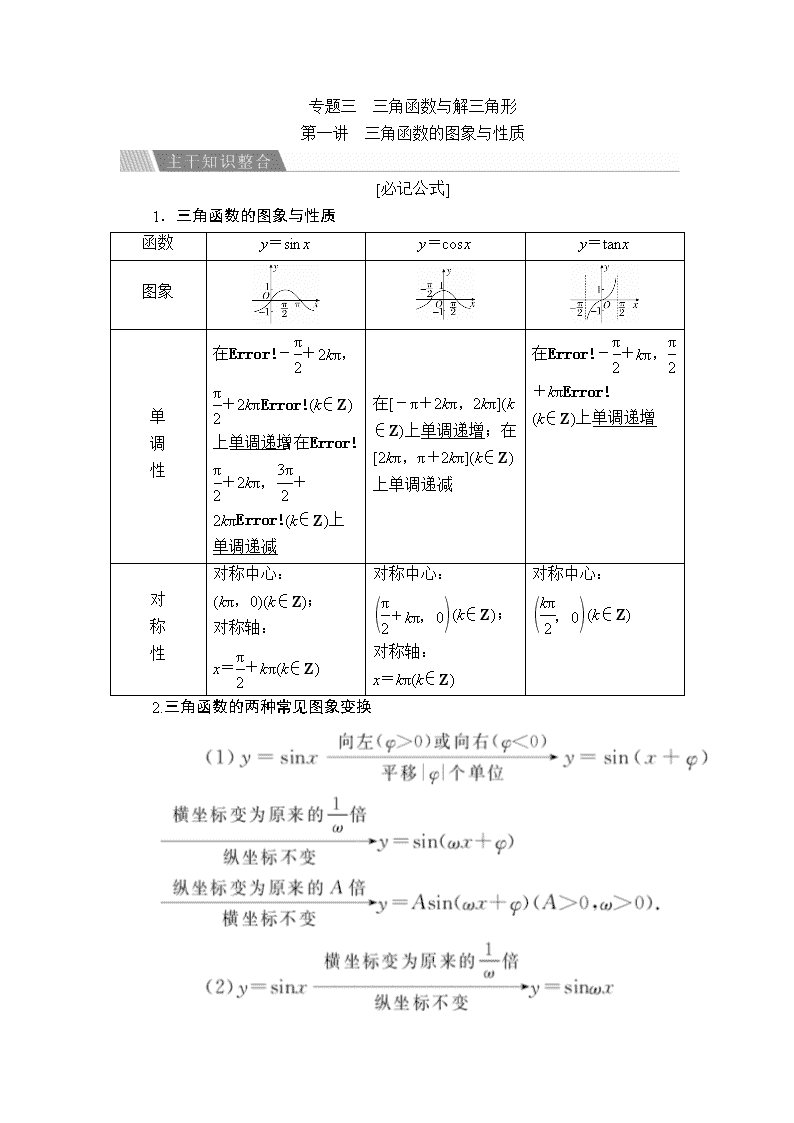
专题三 三角函数与解三角形 第一讲 三角函数的图象与性质 [必记公式] 1.三角函数的图象与性质 函数 y=sinx y=cosx y=tanx 图象 单 调 性 在-+2kπ,+2kπ(k∈Z)上单调递增;在+2kπ,+2kπ(k∈Z)上单调递减 在[-π+2kπ,2kπ](k∈Z)上单调递增;在[2kπ,π+2kπ](k∈Z)上单调递减 在-+kπ,+kπ (k∈Z)上单调递增 对 称 性 对称中心: (kπ,0)(k∈Z); 对称轴: x=+kπ(k∈Z) 对称中心: (k∈Z); 对称轴: x=kπ(k∈Z) 对称中心: (k∈Z) 2.三角函数的两种常见图象变换 [重要结论] 1.三角函数的奇偶性 (1)函数y=Asin(ωx+φ)是奇函数⇔φ=kπ(k∈Z),是偶函数⇔φ=kπ+(k∈Z); (2)函数y=Acos(ωx+φ)是奇函数⇔φ=kπ+(k∈Z),是偶函数⇔φ=kπ(k∈Z); (3)函数y=Atan(ωx+φ)是奇函数⇔φ=kπ(k∈Z). 2.三角函数的对称性 (1)函数y=Asin(ωx+φ)的图象的对称轴由ωx+φ=kπ+(k∈Z)解得,对称中心的横坐标由ωx+φ=kπ(k∈Z)解得; (2)函数y=Acos(ωx+φ)的图象的对称轴由ωx+φ=kπ(k∈Z)解得,对称中心的横坐标由ωx+φ=kπ+(k∈Z)解得; (3)函数y=Atan(ωx+φ)的图象的对称中心由ωx+φ=(k∈Z)解得. [失分警示] 1.忽视定义域 求解三角函数的单调区间、最值(值域)以及作图象等问题时,要注意函数的定义域. 2.重要图象变换顺序 在图象变换过程中,注意分清是先相位变换,还是先周期变换.变换只是相对于其中的自变量x而言的,如果x的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向. 3.忽视A,ω的符号 在求y=Asin(ωx+φ)的单调区间时,要特别注意A和ω的符号,若ω<0,需先通过诱导公式将x的系数化为正的. 4.易忽略对隐含条件的挖掘,扩大角的范围导致错误. 考点 三角函数的定义域、值域(最值) 典例示法 典例1 (1)[2016·合肥一模]函数y=lg (2sinx-1)+的定义域是________. [解析] 由题意,得即 首先作出sinx=与cosx=表示的角的终边(如图所示). 由图可知劣弧和优弧的公共部分对应角的范围是,2kπ+(k∈Z). 所以函数的定义域为(k∈Z). [答案] (k∈Z) (2)已知函数f(x)=-sin+6sinxcosx-2cos2x+1,x∈R. ①求f(x)的最小正周期; ②求f(x)在区间上的最大值和最小值. [解] ①f(x)=-sin2x-cos2x+3sin2x-cos2x=2sin2x-2cos2x=2sin. 所以f(x)的最小正周期T==π. ②由①知f(x)=2sin. 因为x∈, 所以2x-∈, 则sin∈. 所以f(x)在上最大值为2,最小值为-2. 1.三角函数定义域的求法 求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解. 2.三角函数值域(最值)的三种求法 (1)直接法:利用sinx,cosx的值域. (2)化一法:化为y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域(最值). (3)换元法:把sinx或cosx看作一个整体,可化为求函数在给定区间上的值域(最值)问题. 针对训练 [2015·天津高考]已知函数f(x)=sin2x-sin2,x∈R. (1)求f(x)的最小正周期; (2)求f(x)在区间上的最大值和最小值. 解 (1)由已知,有 f(x)=- =-cos2x =sin2x-cos2x=sin. 所以,f(x)的最小正周期T==π. (2)解法一:因为f(x)在区间上是减函数,在区间上是增函数, f=-,f=-,f=.所以,f(x)在区间[-,]上的最大值为,最小值为-. 解法二:由x∈得2x-∈,故当2x-=-,x=-时,f(x)取得最小值为-,当2x-=,x=时,f(x)取最大值为. 考点 三角函数的性质 典例示法 典例2 [2015·山东枣庄质检]已知函数f(x)=sin+sin-2cos2,x∈R(其中ω>0). (1)求函数f(x)的值域; (2)若函数f(x)的图象与直线y=-1的两个相邻交点间的距离为,求函数f(x)的单调递增区间. [解] (1)f(x)=sinωx+cosωx+sinωx-cosωx-(cosωx+1) =2-1 =2sin-1 由-1≤sin≤1, 得-3≤2sin-1≤1, 所以函数f(x)的值域为[-3,1]. (2)由题设条件及三角函数的图象和性质可知, f(x)的周期为π,所以=π,即ω=2. 所以f(x)=2sin-1, 再由2kπ-≤2x-≤2kπ+(k∈Z), 解得kπ-≤x≤kπ+(k∈Z). 所以函数f(x)的单调递增区间为 (k∈Z). 1.求解函数y=Asin(ωx+φ)的性质问题的三种意识 (1)转化意识:利用三角恒等变换将所求函数转化为f(x)=Asin(ωx+φ)的形式. (2)整体意识:类比y=sinx的性质,只需将y=Asin(ωx+φ)中的“ωx+φ”看成y=sinx中的“x”,采用整体代入求解. ①令ωx+φ=kπ+(k∈Z),可求得对称轴方程. ②令ωx+φ=kπ(k∈Z),可求得对称中心的横坐标. ③将ωx+φ看作整体,可求得y=Asin(ωx+φ)的单调区间,注意ω的符号. (3)讨论意识:当A为参数时,求最值应分情况讨论A>0,A<0. 2.求解三角函数的性质的三种方法 (1)求单调区间的两种方法 ①代换法:求形如y=Asin(ωx+φ)(或y=Acos(ωx+φ))(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=z,则y=Asinz(或y=Acosz),然后由复合函数的单调性求得. ②图象法:画出三角函数的图象,结合图象求其单调区间. (2)判断对称中心与对称轴:利用函数y=Asin(ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断. (3)三角函数周期的求法 ①利用周期定义. ②利用公式:y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为. ③利用图象. 针对训练 1.[2015·湖南高考]已知ω>0,在函数y=2sinωx与y=2cosωx的图象的交点中,距离最短的两个交点的距离为2,则ω=________. 答案 解析 由题意,两函数图象交点间的最短距离即相邻的两交点间的距离,设相邻的两交点坐标分别为P(x1,y1),Q(x2,y2),易知|PQ|2=(x2-x1)2+(y2-y1)2,其中|y2-y1|=-(-)=2,|x2-x1|为函数y=2sinωx-2cosωx=2sin的两个相邻零点之间的距离,恰好为函数最小正周期的一半,所以(2)2=2+(2)2,ω=. 2.[2014·北京高考]设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间上具有单调性,且f=f=-f,则f(x)的最小正周期为________. 答案 π 解析 由f(x)在区间上具有单调性,且f=-f知,f(x)有对称中心,由f=f知f(x)有对称轴x=(+π)=π.记f(x)的最小正周期为T,则T≥-,即T≥π.故π-==,解得T=π. 考点 三角函数的图象及应用 典例示法 题型1 利用图象求y=Asin(ωx+φ)的解析式 典例3 函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是( ) A.2,- B.2,- C.4,- D.4, [解析] 从图中读出此函数的周期情况为T=·=-=,所以ω =2.又读出图中最高点坐标为,代入解析式f(x)=2sin(2x+φ),得到2=2sin,所以2×+φ=2kπ+(k∈Z),则φ=2kπ-. 因为-<φ<,所以令k=0,得到φ=-,故选A. [答案] A 题型2 函数y=Asin(ωx+φ)的图象变换 典例4 [2015·山东高考]要得到函数y=sin的图象,只需将函数y=sin4x的图象( ) A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位 [解析] 因为y=sin=sin,所以只需将y=sin4x的图象向右平移个单位,即可得到函数y=sin的图象,故选B. [答案] B 题型3 函数y=Asin(ωx+φ)的图象和性质的综合应用 典例5 [2016·太原一模]已知函数f(x)=sin(ωx+φ)的最小正周期是π,若将其图象向右平移个单位后得到的图象关于原点对称,则函数f(x)的图象( ) A.关于直线x=对称 B.关于直线x=对称 C.关于点对称 D.关于点对称 [解析] ∵f(x)的最小正周期为π,∴=π,ω=2,∴f(x)的图象向右平移个单位后得到g(x)=sin=sin的图象,又g(x)的图象关于原点对称, ∴-+φ=kπ,k∈Z,φ=+kπ,k∈Z,又|φ|<,∴<,∴k=-1,φ=- ,∴f(x)=sin,当x=时,2x-=-,∴A,C错误,当x=时,2x-=,∴B正确,D错误. [答案] B 本例中条件不变,若平移后得到的图象关于y轴对称,则f(x)的图象又关于谁对称?( ) 答案 D 解析 g(x)的图象关于y轴对称,则-+φ=+kπ,k∈Z,可求φ=,∴f(x)=sin,2x+=kπ,可得x=-,令k=1,则x=,故选D. 1.函数表达式y=Asin(ωx+φ)+B的确定方法 2.三角函数图象平移问题处理策略 (1)看平移要求:首先要看题目要求由哪个函数平移得到哪个函数,这是判断移动方向的关键点. (2)看移动方向:移动的方向一般记为“正向左,负向右”,看y=Asin(ωx+φ)中φ的正负和它的平移要求. (3)看移动单位:在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系,φ是初相,再经过ω的压缩,最后移动的单位是. 3.研究三角函数图象与性质的常用方法 (1)求三角函数的周期、单调区间、最值及判断三角函数的奇偶性,往往是在定义域内,先化简三角函数式,尽量化为y=Asin(ωx+φ)的形式,然后再求解. (2)对于形如y=asinωx+bcosωx型的三角函数,要通过引入辅助角化为y=sin(ωx+φ),的形式来求. [全国卷高考真题调研] 1.[2016·全国卷Ⅱ]若将函数y=2sin2x的图象向左平移个单位长度,则平移后图象的对称轴为( ) A.x=-(k∈Z) B.x=+(k∈Z) C.x=-(k∈Z) D.x=+(k∈Z) 答案 B 解析 函数y=2sin2x的图象向左平移个单位长度,得到的图象对应的函数表达式为y=2sin,令2=kπ+(k∈Z),解得x=+(k∈Z),所以所求对称轴的方程为x=+(k∈Z),故选B. 2.[2015·全国卷Ⅰ]函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( ) A.,k∈Z B.,k∈Z C.,k∈Z D.,k∈Z 答案 D 解析 由图象可知+φ=+2mπ,+φ=+2mπ,m∈Z,所以ω=π,φ=+2mπ,m∈Z,所以函数f(x)=cos=cos的单调递减区间为2kπ<πx+<2kπ+π,k∈Z,即2k-查看更多