2017-2018学年天津市滨海新区大港八中高二上学期第二次月考数学试题（文科）（解析版）

2017-2018学年天津市滨海新区大港八中高二上学期第二次月考数学试题（文科）（解析版）

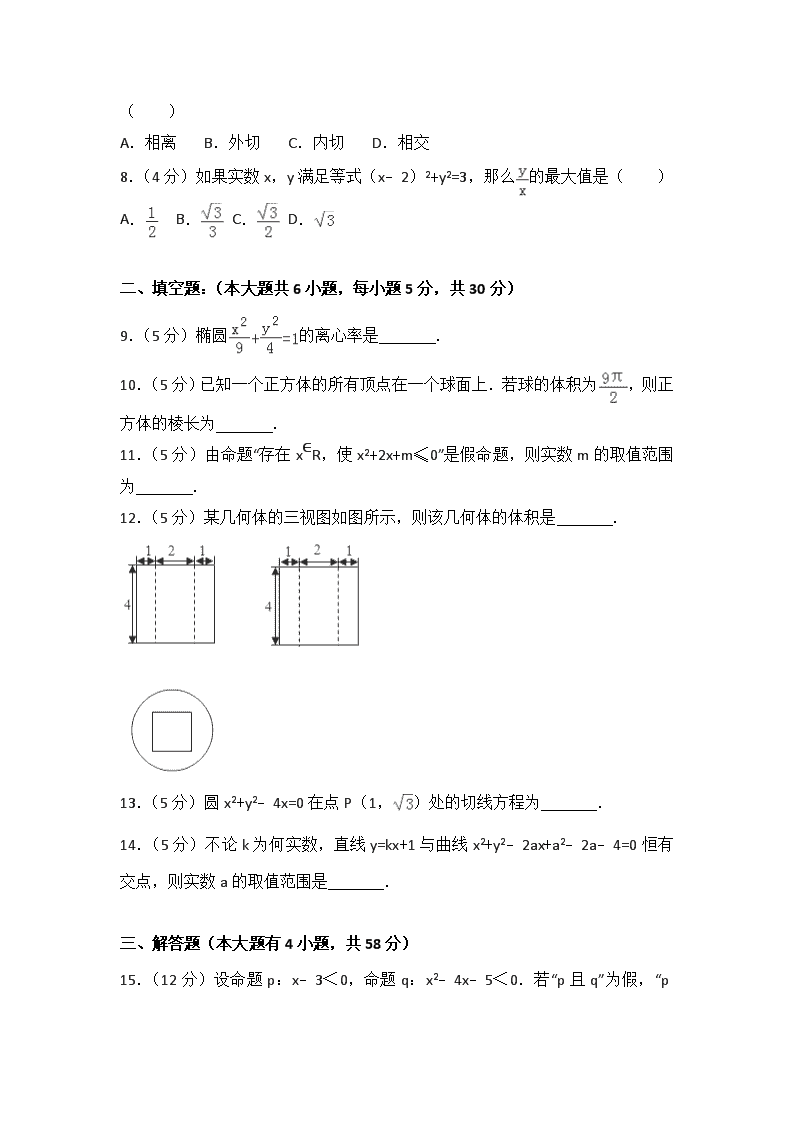
‎2017-2018学年天津市滨海新区大港八中高二（上）第二次月考数学试卷（文科）‎ ‎　‎ 一、选择题：（本大题共8小题，每小题4分，共32分）‎ ‎1．（4分）过点（1，2），且与直线x+2y+2=0垂直的直线方程为（　　）‎ A．2x﹣y=0 B．x﹣2y+3=0 C．2x+y﹣4=0 D．x+2y﹣5=0‎ ‎2．（4分）已知命题P：“∀x∈R，x2+2x+3≥0”，则命题P的否定为（　　）‎ A．∀x∈R，x2+2x+3＜0 B．∃x∈R，x2+2x+3≥0‎ C．∃x∈R，x2+2x+3＜0 D．∃x∈R，x2+2x+3≤0‎ ‎3．（4分）已知两条直线L1：3x+2y+5=0，L2：（m2﹣1）x+2y﹣3=0，则“m=2”是“L1∥L2”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎4．（4分）在空间直角坐标系中，P（2，3，4）、Q（﹣2，﹣3，﹣4）两点的位置关系是（　　）‎ A．关于x轴对称 B．关于yoz平面对称 C．关于坐标原点对称 D．以上都不对 ‎5．（4分）设l为直线，α，β是两个不同的平面，下列命题中正确的是（　　）‎ A．若l∥α，l∥β，则α∥β B．若l⊥α，l⊥β，则α∥β C．若l⊥α，l∥β，则α∥β D．若α⊥β，l∥α，则l⊥β ‎6．（4分）有下列四个命题，其中真命题有：‎ ‎①“若x+y=0，则x、y互为相反数”的逆命题 ‎②“全等三角形的面积相等”的否命题 ‎③“若q≤1，则x2+2x+q=0有实根”的逆命题 ‎④“不等边三角形的三个内角相等”的逆否命题，其中真命题的序号为（　　）‎ A．①③ B．②③ C．①② D．③④‎ ‎7．（4分）圆C1：x2+y2+2x+8y﹣8=0与圆C2：x2+y2﹣4x+‎ ‎4y﹣2=0的位置关系是（　　）‎ A．相离 B．外切 C．内切 D．相交 ‎8．（4分）如果实数x，y满足等式（x﹣2）2+y2=3，那么的最大值是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题：（本大题共6小题，每小题5分，共30分）‎ ‎9．（5分）椭圆的离心率是　 　．‎ ‎10．（5分）已知一个正方体的所有顶点在一个球面上．若球的体积为，则正方体的棱长为　 　．‎ ‎11．（5分）由命题“存在x∈R，使x2+2x+m≤0”是假命题，则实数m的取值范围为　 　．‎ ‎12．（5分）某几何体的三视图如图所示，则该几何体的体积是　 　．‎ ‎13．（5分）圆x2+y2﹣4x=0在点P（1，）处的切线方程为　 　．‎ ‎14．（5分）不论k为何实数，直线y=kx+1与曲线x2+y2﹣2ax+a2﹣2a﹣4=0恒有交点，则实数a的取值范围是　 　．‎ ‎　‎ 三、解答题（本大题有4小题，共58分）‎ ‎15．（12分）设命题p：x﹣3＜0，命题q：x2﹣4x﹣5＜‎ ‎0．若“p且q”为假，“p或q”为真，求实数x的取值范围．‎ ‎16．（13分）如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，已知AB=3，AD=2，PA=2，PD=2，∠PAB=60°‎ ‎（Ⅰ）证明AD⊥平面PAB；‎ ‎（Ⅱ）求异面直线PC与AD所成的角的正切值；‎ ‎（Ⅲ）求四棱锥P﹣ABCD的体积．‎ ‎17．（15分）已知过点M（﹣3，﹣3）的直线l被圆x2+y2+4y﹣21=0所截得的弦长为4．‎ ‎（Ⅰ）求圆的圆心C及其半径r；‎ ‎（Ⅱ）求直线l的方程．‎ ‎18．（18分）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．‎ ‎（Ⅰ）证明：EF∥平面A1CD；‎ ‎（Ⅱ）证明：平面A1CD⊥平面A1ABB1；‎ ‎（Ⅲ）求直线BC与平面A1CD所成角的正弦值．‎ ‎　‎ ‎2017-2018学年天津市滨海新区大港八中高二（上）第二次月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：（本大题共8小题，每小题4分，共32分）‎ ‎1．（4分）过点（1，2），且与直线x+2y+2=0垂直的直线方程为（　　）‎ A．2x﹣y=0 B．x﹣2y+3=0 C．2x+y﹣4=0 D．x+2y﹣5=0‎ ‎【分析】与直线x+2y+2=0垂直的直线方程的斜率k=2，由此能求出过点P（1，2）与直线x+2y+2=0垂直的直线方程．‎ ‎【解答】解：∵与直线x+2y+2=0垂直的直线方程的斜率k=2，‎ ‎∴过点P（1，2）与直线x+2y+2=0垂直的直线方程为：y﹣2=2（x﹣1），‎ 整理，得2x﹣y=0．‎ 故选：A ‎【点评】本题考查直线方程的求法，是基础题，解题时要认真审题，注意直线与直线垂直的性质的合理运用 ‎　‎ ‎2．（4分）已知命题P：“∀x∈R，x2+2x+3≥0”，则命题P的否定为（　　）‎ A．∀x∈R，x2+2x+3＜0 B．∃x∈R，x2+2x+3≥0‎ C．∃x∈R，x2+2x+3＜0 D．∃x∈R，x2+2x+3≤0‎ ‎【分析】据命题否定的规则，对命题“∀x∈R，x2+2x+3≥0”进行否定，注意任意对应的否定词为存在；‎ ‎【解答】解：根据全称命题的否定是特称命题可知：∀x∈R，x2+2x+3≥0的否定为∃x∈R，x2+2x+3＜0‎ 故选C ‎【点评】题主要考查命题的否定及其书写规则，此题是一道基础题，要注意对任意的否定是存在 ‎　‎ ‎3．（4分）已知两条直线L1：3x+2y+5=0，L2：（m2﹣1）x+2y﹣3=0，则“m=2”是“L1∥L2”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【分析】由2（m2﹣1）﹣6=0，解得m，再经过验证两条直线是否平行，即可得出a的取值范围，进而判断出结论．‎ ‎【解答】解：由2（m2﹣1）﹣6=0，解得m=±2，‎ 解得验证：m=±2时，两条直线都平行，因此m=±2．‎ ‎∴“m=2”是“L1∥L2”的充分不必要条件．‎ 故选：A．‎ ‎【点评】本题考查了直线平行的充要条件、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎4．（4分）在空间直角坐标系中，P（2，3，4）、Q（﹣2，﹣3，﹣4）两点的位置关系是（　　）‎ A．关于x轴对称 B．关于yoz平面对称 C．关于坐标原点对称 D．以上都不对 ‎【分析】若两点的横坐标、纵坐标、竖坐标都关于坐标原点对称，则两点的位置关系是关于坐标原点对称 ‎【解答】解：在空间直角坐标系中，P（2，3，4）、Q（﹣2，﹣3，﹣4），‎ ‎∵两点的横坐标、纵坐标、竖坐标都关于坐标原点对称，‎ ‎∴两点的位置关系是关于坐标原点对称．‎ 故选：C．‎ ‎【点评】本题考查空间中两点位置关系的判断，是基础题，解题时要认真审题，注意空间直角坐标系的合理运用．‎ ‎　‎ ‎5．（4分）设l为直线，α，β是两个不同的平面，下列命题中正确的是（　　）‎ A．若l∥α，l∥β，则α∥β B．若l⊥α，l⊥β，则α∥β C．若l⊥α，l∥β，则α∥β D．若α⊥β，l∥α，则l⊥β ‎【分析】根据线面平行的几何特征及面面平行的判定方法，可判断A；‎ 根据面面平行的判定方法及线面垂直的几何特征，可判断B；‎ 根据线面平行的性质定理，线面垂直及面面垂直的判定定理，可判断C；‎ 根据面面垂直及线面平行的几何特征，可判断D．‎ ‎【解答】解：若l∥α，l∥β，则平面α，β可能相交，此时交线与l平行，故A错误；‎ 若l⊥α，l⊥β，根据垂直于同一直线的两个平面平行，可得B正确；‎ 若l⊥α，l∥β，则存在直线m⊂β，使l∥m，则m⊥α，故此时α⊥β，故C错误；‎ 若α⊥β，l∥α，则l与β可能相交，可能平行，也可能线在面内，故D错误；‎ 故选B ‎【点评】本题考查的知识点是空间中直线与直线的位置关系，直线与平面的位置关系及平面与平面之间的位置关系，熟练掌握空间线面关系的几何特征及判定方法是解答的关键．‎ ‎　‎ ‎6．（4分）有下列四个命题，其中真命题有：‎ ‎①“若x+y=0，则x、y互为相反数”的逆命题 ‎②“全等三角形的面积相等”的否命题 ‎③“若q≤1，则x2+2x+q=0有实根”的逆命题 ‎④“不等边三角形的三个内角相等”的逆否命题，其中真命题的序号为（　　）‎ A．①③ B．②③ C．①② D．③④‎ ‎【分析】①原命题的逆命题为“若x与y互为相反数，则x+y=0”，即可判断出正误；‎ ‎②原命题的否命题为：“不全等三角形的面积不相等”，不正确；‎ ‎③原命题的逆命题为“若x2+2x+q=0有实根，则q≤1”，由△≥0，解得q≤1，即可判断出正误；‎ ‎④原命题的逆否命题：“三个内角不相等的三角形是等边三角形”，利用等边三角形的定义即可判断出正误．‎ ‎【解答】解：①“若x+‎ y=0，则x与y互为相反数”的逆命题为“若x与y互为相反数，则x+y=0”，正确；‎ ‎②“全等三角形的面积相等”的否命题为：“不全等三角形的面积不相等”，不正确；‎ ‎③“若q≤1，则x2+2x+q=0有实根”的逆命题为“若x2+2x+q=0有实根，则q≤1”，由△=4﹣4q≥0，解得q≤1，因此正确；‎ ‎④“不等边三角形的三个内角相等”的逆否命题：“三个内角不相等的三角形是等边三角形”，是假命题．‎ 故选：A．‎ ‎【点评】本题考查了简易逻辑的判定方法、一元二次方程的实数根与判别式的关系等基础知识，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎7．（4分）圆C1：x2+y2+2x+8y﹣8=0与圆C2：x2+y2﹣4x+4y﹣2=0的位置关系是（　　）‎ A．相离 B．外切 C．内切 D．相交 ‎【分析】把两圆的方程化为标准形式，求出圆心坐标和半径，求出两圆的圆心距，根据两圆的圆心距大于两圆的半径之差小于半径之和，判断两圆相交．‎ ‎【解答】解：圆C1：x2+y2+2x+8y﹣8=0 即 （x+1）2+（y+4）2=25，表示以A（﹣1，﹣4）为圆心，以5为半径的圆．‎ C2：x2+y2﹣4x+4y﹣2=0 即 （x﹣2）2+（y+2）2=10，表示以A（2，﹣2）为圆心，以为半径的圆．‎ ‎ 两圆的圆心距d==，大于两圆的半径之差小于半径之和，故两圆相交，‎ 故选 D．‎ ‎【点评】本题考查两圆的位置关系，利用两圆的圆心距大于两圆的半径之差小于半径之和，故两圆相交．‎ ‎　‎ ‎8．（4分）如果实数x，y满足等式（x﹣2）2+y2=3，那么的最大值是（　　）‎ A． B． C． D．‎ ‎【分析】表示圆上动点与原点O连线的斜率，画出满足等式（x﹣2）2+y2‎ ‎=3的图形，由数形结合，我们易求出的最大值．‎ ‎【解答】解：满足等式（x﹣2）2+y2=3的图形如图所示：‎ 表示圆上动点与原点O连线的斜率，‎ 由图可得动点与B重合时，此时OB与圆相切，取最大值，‎ 连接BC，在Rt△OBC中，BC=，OC=2‎ 易得∠BOC=60°‎ 此时=‎ 故选D ‎【点评】本题考查的知识点是简单线性规划，分析出表示圆上动点与原点O连线的斜率，是解答本题的关键．‎ ‎　‎ 二、填空题：（本大题共6小题，每小题5分，共30分）‎ ‎9．（5分）椭圆的离心率是　　．‎ ‎【分析】利用题意的标准方程，求出a，b，然后求解c，即可求解题意的离心率即可．‎ ‎【解答】解：椭圆的长半轴为a=3，短半轴为b=2，则半焦距为c==．‎ 所以椭圆的离心率为：e==．‎ 故答案为：．‎ ‎【点评】本题考查椭圆的简单性质的应用，离心率的求法，是基础题．‎ ‎　‎ ‎10．（5分）已知一个正方体的所有顶点在一个球面上．若球的体积为，则正方体的棱长为　　．‎ ‎【分析】设出正方体棱长，利用正方体的体对角线就是外接球的直径，通过球的体积求出正方体的棱长．‎ ‎【解答】解：因为正方体的体对角线就是外接球的直径，‎ 设正方体的棱长为a，所以正方体的体对角线长为：a，正方体的外接球的半径为：，‎ 球的体积为：，‎ 解得a=．‎ 故答案为：．‎ ‎【点评】本题考查正方体与外接球的关系，注意到正方体的体对角线就是球的直径是解题的关键，考查空间想象能力与计算能力．‎ ‎　‎ ‎11．（5分）由命题“存在x∈R，使x2+2x+m≤0”是假命题，则实数m的取值范围为　（1，+∞）　．‎ ‎【分析】原命题为假命题，则其否命题为真命题，得出∀x∈R，都有x2+2x+m＞0，再由△＜0，求得m．‎ ‎【解答】解：∵“存在x∈R，使x2+2x+m≤0”，‎ ‎∴其否命题为真命题，即是说“∀x∈R，都有x2+2x+m＞0”，‎ ‎∴△=4﹣4m＜0，‎ 解得m＞1．‎ ‎∴m的取值范围为（1，+∞）．‎ 故答案为：（1，+∞）‎ ‎【点评】本题考查了存在命题的否定，不等式恒成立问题．考查转化、计算能力．‎ ‎　‎ ‎12．（5分）某几何体的三视图如图所示，则该几何体的体积是　16π﹣16　．‎ ‎【分析】首先判断该几何体的形状，然后计算其体积即可．‎ ‎【解答】解：根据三视图可知，该几何体为圆柱中挖去一个四棱柱，‎ 圆柱是底面外径为2，高为4的圆筒，‎ 四棱柱的底面是边长为2的正方形，高也为4．‎ 故其体积为：22π×4﹣22×4=16π﹣16，‎ 故答案为：16π﹣16．‎ ‎【点评】本题考查了由三视图判断几何体的知识，解题的关键是首先判断该几何体为圆柱中挖去一个棱柱，然后利用柱体的体积计算方法计算其体积差即可．‎ ‎　‎ ‎13．（5分）圆x2+y2﹣4x=0在点P（1，）处的切线方程为　x﹣y+2=0　．‎ ‎【分析】求出圆的圆心坐标，求出切点与圆心连线的斜率，然后求出切线的斜率，解出切线方程．‎ ‎【解答】解：圆x2+y2﹣4x=0的圆心坐标是（2，0），‎ 所以切点与圆心连线的斜率：=﹣，‎ 所以切线的斜率为：，‎ 切线方程为：y﹣=（x﹣1），‎ 即x﹣y+2=0．‎ 故答案为：x﹣y+2=0．‎ ‎【点评】本题是基础题，考查圆的切线方程的求法，求出切线的斜率解题的关键，考查计算能力．‎ ‎　‎ ‎14．（5分）不论k为何实数，直线y=kx+1与曲线x2+y2﹣2ax+a2﹣2a﹣4=0恒有交点，则实数a的取值范围是　﹣1≤a≤3　．‎ ‎【分析】直线y=kx+1与曲线x2+y2﹣2ax+a2﹣2a﹣4=0恒有交点，说明直线系过的定点必在圆上或圆内．‎ ‎【解答】解：直线y=kx+1恒过（0，1）点的直线系，‎ 曲线x2+y2﹣2ax+a2﹣2a﹣4=0表示圆圆心（a，0），半径为：），‎ 直线与曲线x2+y2﹣2ax+a2﹣2a﹣4=0恒有交点，必须定点在圆上或圆内，‎ 即：所以，﹣1≤a≤3‎ 故答案为：﹣1≤a≤3．‎ ‎【点评】本题考查直线与圆的位置关系，点与圆的位置关系，两点间的距离公式，直线系等知识是中档题．‎ ‎　‎ 三、解答题（本大题有4小题，共58分）‎ ‎15．（12分）设命题p：x﹣3＜0，命题q：x2﹣4x﹣5＜0．若“p且q”为假，“p或q”为真，求实数x的取值范围．‎ ‎【分析】分别求出p，q为真时的x的范围，根据p真q假、p假q真得到关于x的不等式组，解出即可．‎ ‎【解答】解：命题p为真，则有x＜3；‎ 命题q为真，则有x2﹣4x﹣5＜0，解得﹣1＜x＜5．‎ 由“p或q为真，p且q为假”可知p和q满足：‎ p真q假、p假q真．所以应有或 解得x≤﹣1或3≤x＜5‎ 此即为当“p或q为真，p且q为假”时实数a的取值范围为（﹣∞，﹣1]∪[3，5）．‎ ‎【点评】本题考查了复合命题的判断，考查解不等式问题，是一道基础题．‎ ‎　‎ ‎16．（13分）如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，已知AB=3，AD=2，PA=2，PD=2，∠PAB=60°‎ ‎（Ⅰ）证明AD⊥平面PAB；‎ ‎（Ⅱ）求异面直线PC与AD所成的角的正切值；‎ ‎（Ⅲ）求四棱锥P﹣ABCD的体积．‎ ‎【分析】（I）由题意在△PAD中，利用所给的线段长度计算出AD⊥PA，再利用矩形ABCD及线面垂直的判定定理即可证明线面垂直．‎ ‎（II）利用条件借助图形，利用异面直线所成角的定义找到共面的两条相交直线，然后结合解三角形有关知识解出即可；‎ ‎（Ⅲ）过点P做PH⊥AB于H，因为平面PAB⊥平面ABCD平面PAB∩平面ABCD=AB，所以PH⊥平面ABCD，由题意得求三棱锥的高PH=．可得三棱锥的体积是 ．‎ ‎【解答】解：（Ⅰ）证明：在△PAD中，由题设PA=2，PD=2 ，‎ 可得PA2+AD2=PD2于是AD⊥PA．‎ 在矩形ABCD中，AD⊥AB．又PA∩AB=A，‎ 所以AD⊥平面PAB．‎ ‎（Ⅱ）由题设，BC∥AD，‎ 所以∠PCB（或其补角）是异面直线PC与AD所成的角．‎ 在△PAB中，由余弦定理得 PB=‎ 由（Ⅰ）知AD⊥平面PAB，PB⊂平面PAB，‎ 所以AD⊥PB，因而BC⊥PB，于是△PBC是直角三角形，故tanPCB=．‎ 所以异面直线PC与AD所成的角的大小为arctan ．‎ ‎（Ⅲ）过点P做PH⊥AB于H，‎ ‎∵平面PAB⊥平面ABCD平面PAB∩平面ABCD=AB ‎∴PH⊥平面ABCD，‎ 在Rt△PHA中PH=PAsin60°=‎ ‎∴‎ ‎【点评】本小题主要考查直线和平面垂直，异面直线所成的角，以及求三棱锥的体积关键是找到一个高并且简单易求，考查空间想象能力，运算能力和推理论证能力，还考查了利用反三角函数的知识求出角的大小．‎ ‎　‎ ‎17．（15分）已知过点M（﹣3，﹣3）的直线l被圆x2+y2+4y﹣21=0所截得的弦长为4．‎ ‎（Ⅰ）求圆的圆心C及其半径r；‎ ‎（Ⅱ）求直线l的方程．‎ ‎【分析】（Ⅰ）化简圆的方程为标准方程，然后推出圆的圆心C及其半径r；‎ ‎（Ⅱ）通过直线的斜率是否存在，设出直线方程，然后利用点到直线的距离公式转化求解即可．‎ ‎【解答】解：（Ⅰ）将圆的方程写成标准形式，得x2+（y+2）2=25，‎ 所以圆心的坐标是（0，﹣2），半径长r=5，弦心距为：=，‎ ‎（Ⅱ）当k存在时，由题意设所求直线方程为y+3=k（x+3），因此，‎ 所以|3k﹣1|=，即2k2﹣3k﹣2=0，‎ 解得k=﹣或k=2，‎ 故所求直线方程为x+2y+9=0或2x﹣y+3=0．‎ 当k不存在时，直线方程为x=﹣3，弦心距为3，弦长为2，与已知不符（舍）‎ 所以直线l的方程为x+2y+9=0或2x﹣y+3=0．‎ ‎【点评】本题考查直线与圆的方程的应用，考查转化思想以及计算能力．‎ ‎　‎ ‎18．（18分）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．‎ ‎（Ⅰ）证明：EF∥平面A1CD；‎ ‎（Ⅱ）证明：平面A1CD⊥平面A1ABB1；‎ ‎（Ⅲ）求直线BC与平面A1CD所成角的正弦值．‎ ‎【分析】（I）连接ED，要证明EF∥平面平面A1CD，只需证明EF∥DA1即可；‎ ‎（II）欲证平面平面A1CD⊥平面A1ABB1，即证平面内一直线与另一平面垂直，根据直线与平面垂直的判定定理证得CD⊥面A1ABB1，再根据面面垂直的判定定理得证；‎ ‎（III）先过B作BG⊥AD交A1D于G，利用（II）中结论得出BG⊥面A1CD，从而∠BCG为所求的角，最后在直角△BGC中，求出sin∠BCG即可得出直线BC与平面A1CD所成角的正弦值．‎ ‎【解答】证明：（I）三棱柱ABC﹣A1B1C1中，AC∥A1C1，AC=A1C1，连接ED，‎ 可得DE∥AC，DE=AC，又F为棱A1C1的中点．∴A1F=DE，A1F∥DE，‎ 所以A1DEF是平行四边形，所以EF∥DA1，‎ DA1⊂平面A1CD，EF⊄平面A1CD，∴EF∥平面A1CD ‎（II）∵D是AB的中点，∴CD⊥AB，‎ 又AA1⊥平面ABC，CD⊂平面ABC，‎ ‎∴AA1⊥CD，又AA1∩AB=A，‎ ‎∴CD⊥面A1ABB1，又CD⊂面A1CD，‎ ‎∴平面A1CD⊥平面A1ABB1；‎ ‎（III）过B作BG⊥A1D交A1D于G，‎ ‎∵平面A1CD⊥平面A1ABB1，且平面A1CD∩平面A1ABB1=A1D，‎ BG⊥A1D，‎ ‎∴BG⊥面A1CD，‎ 则∠BCG为所求的角，‎ 设棱长为a，可得A1D=，由△A1AD∽△BGD，得BG=，‎ 在直角△BGC中，sin∠BCG==，‎ ‎∴直线BC与平面A1CD所成角的正弦值．‎ ‎【点评】本题主要考查了平面与平面垂直的判定，直线与平面所成的角，以及直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于基础题．‎ ‎　‎