2021高考数学一轮复习课时作业38空间几何体的结构及其三视图和直观图文

2021高考数学一轮复习课时作业38空间几何体的结构及其三视图和直观图文

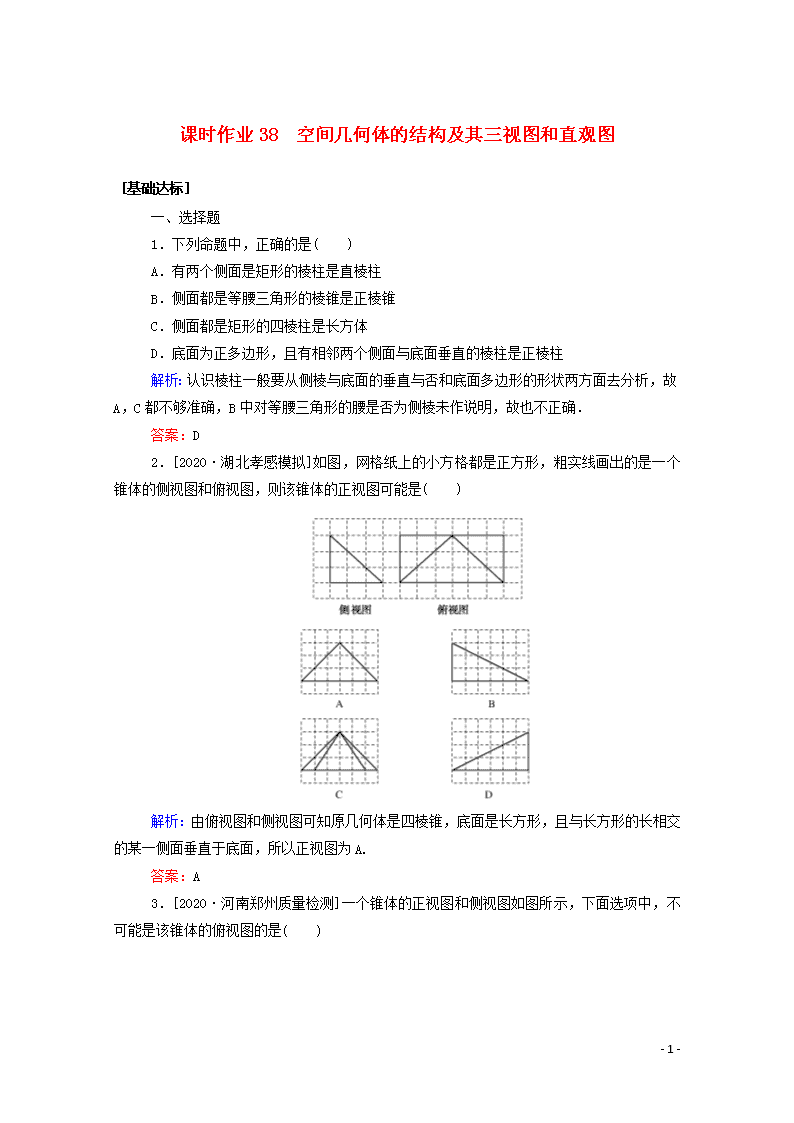
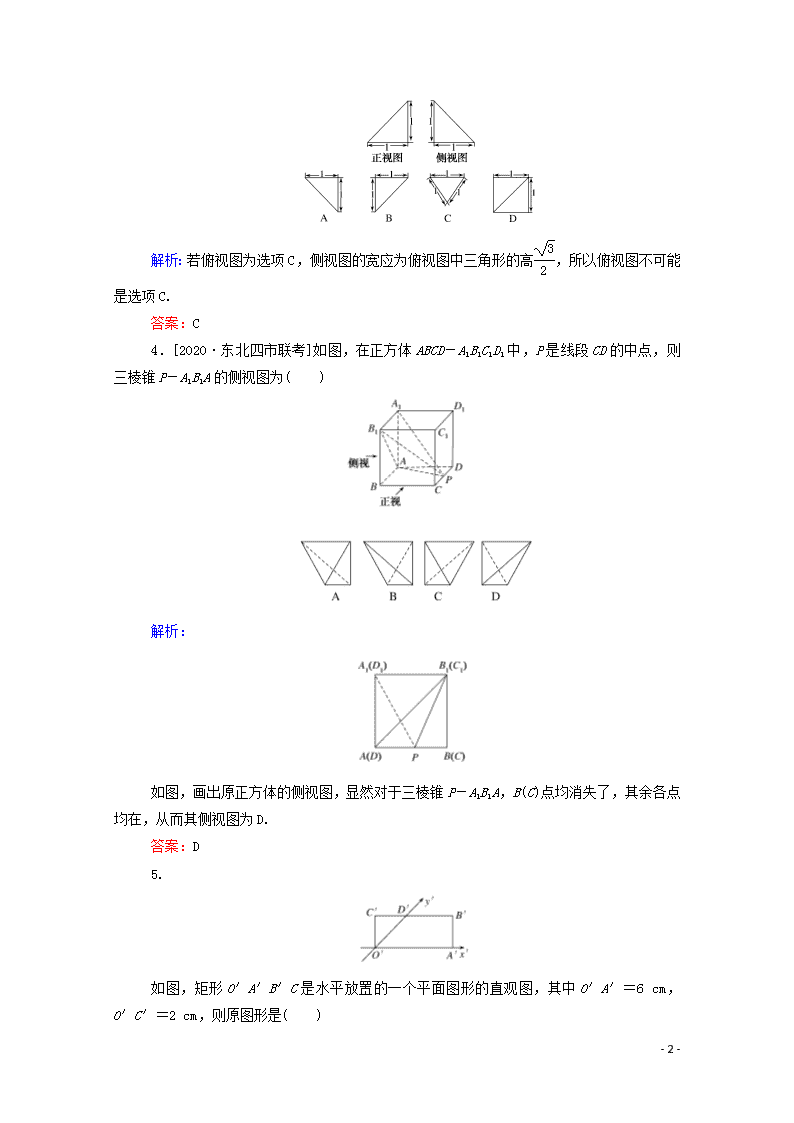
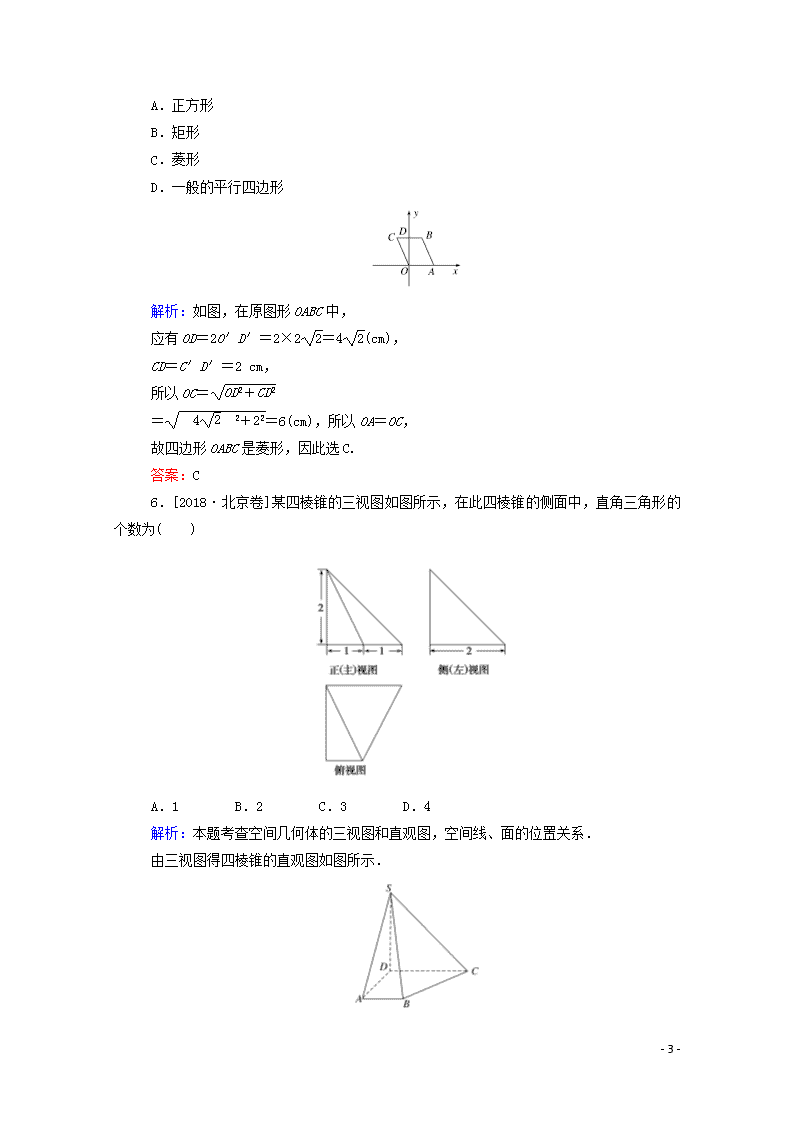
课时作业38　空间几何体的结构及其三视图和直观图 ‎ [基础达标]‎ 一、选择题 ‎1．下列命题中，正确的是(　　)‎ A．有两个侧面是矩形的棱柱是直棱柱 B．侧面都是等腰三角形的棱锥是正棱锥 C．侧面都是矩形的四棱柱是长方体 D．底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱 解析：认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析，故A，C都不够准确，B中对等腰三角形的腰是否为侧棱未作说明，故也不正确．‎ 答案：D ‎2．[2020·湖北孝感模拟]如图，网格纸上的小方格都是正方形，粗实线画出的是一个锥体的侧视图和俯视图，则该锥体的正视图可能是(　　)‎ 解析：由俯视图和侧视图可知原几何体是四棱锥，底面是长方形，且与长方形的长相交的某一侧面垂直于底面，所以正视图为A.‎ 答案：A ‎3．[2020·河南郑州质量检测]一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是(　　)‎ - 9 -‎ 解析：若俯视图为选项C，侧视图的宽应为俯视图中三角形的高，所以俯视图不可能是选项C.‎ 答案：C ‎4．[2020·东北四市联考]如图，在正方体ABCD－A1B1C1D1中，P是线段CD的中点，则三棱锥P－A1B1A的侧视图为(　　)‎ 解析：‎ 如图，画出原正方体的侧视图，显然对于三棱锥P－A1B1A，B(C)点均消失了，其余各点均在，从而其侧视图为D.‎ 答案：D ‎5.‎ 如图，矩形O′A′B′C是水平放置的一个平面图形的直观图，其中O′A′＝6 cm，O′C′＝2 cm，则原图形是(　　)‎ - 9 -‎ A．正方形 ‎ B．矩形 C．菱形 ‎ D．一般的平行四边形 解析：如图，在原图形OABC中，‎ 应有OD＝2O′D′＝2×2＝4(cm)，‎ CD＝C′D′＝2 cm，‎ 所以OC＝ ‎＝＝6(cm)，所以OA＝OC，‎ 故四边形OABC是菱形，因此选C.‎ 答案：C ‎6．[2018·北京卷]某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为(　　)‎ A．1　　　　B．2　　　　C．3　　　　D．4‎ 解析：本题考查空间几何体的三视图和直观图，空间线、面的位置关系．‎ 由三视图得四棱锥的直观图如图所示．‎ - 9 -‎ 其中SD⊥底面ABCD，AB⊥AD，AB∥CD，SD＝AD＝CD＝2，AB＝1.由SD⊥底面ABCD，AD，DC，AB⊂底面ABCD，得SD⊥AD，SD⊥DC，SD⊥AB，故△SDC，△SDA为直角三角形，又∵AB⊥AD，AB⊥SD，AD，SD⊂平面SAD，AD∩SD＝D，∴AB⊥平面SAD，又SA⊂平面SAD，∴AB⊥SA，即△SAB也是直角三角形，从而SB＝＝3，又BC＝＝，SC＝2，∴BC2＋SC2≠SB2，∴△SBC不是直角三角形，故选C.‎ 答案：C ‎7．[2020·山西省八校联考]将正方体(如图1)截去三个三棱锥后，得到如图2所示的几何体，侧视图的视线方向如图2所示，则该几何体的侧视图为(　　)‎ 解析：将图2中的几何体放到正方体中如图所示，从侧视图的视线方向观察，易知该几何体的侧视图为选项D中的图形，故选D.‎ 答案：D ‎8．[2020·河北模拟]某几何体的三视图如图所示，记A为此几何体所有棱的长度构成的集合，则(　　)‎ A．3∈A B．5∈A C．2∈A D．4∈A - 9 -‎ 解析：由三视图可得，该几何体的直观图如图所示，其中底面是边长为4的正方形，AF⊥平面ABCD，AF∥DE，AF＝2，DE＝4，可求得BE的长为4，BF的长为2，EF的长为2，EC的长为4，故选D.‎ 答案：D ‎9．[2020·河南百校联考]如图，网格纸上小正方形的边长为1，图中粗线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为(　　)‎ A．2 B．3‎ C. D. 解析：根据三视图，利用棱长为2的正方体分析知，该多面体是一个三棱锥，即三棱锥A1－MNP，如图所示，其中M，N，P是棱长为2的正方体相应棱的中点，可得棱A1M最长，A1M＝＝3，故最长的棱的长度为3，选B.‎ 答案：B ‎10．[2020·江西南昌模拟]如图，在正四棱柱ABCD－A1B1C1D1中，点P是平面A1B1C1D1内一点，则三棱锥P－BCD的正视图与侧视图的面积之比为(　　)‎ - 9 -‎ A．1:1 B．2:1‎ C．2:3 D．3:2‎ 解析：根据题意，三棱锥P－BCD的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高．故三棱锥P－BCD的正视图与侧视图的面积之比为1:1.‎ 答案：A 二、填空题 ‎11．下列说法正确的有________个．‎ ‎(1)有一个面是多边形，其余各面都是三角形的几何体是棱锥．‎ ‎(2)正棱锥的侧面是等边三角形．‎ ‎(3)底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．‎ 解析：(1)错误．棱锥的定义是：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥．而“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”，故此说法是错误的．如图所示的几何体满足此说法，但它不是棱锥，理由是△ADE和△BCF无公共顶点．‎ ‎(2)错误．正棱锥的侧面都是等腰三角形，不一定是等边三角形．‎ ‎(3)错误．由已知条件知，此三棱锥的三个侧面未必全等，所以不一定是正三棱锥．如图所示的三棱锥中有AB＝AD＝BD＝BC＝CD.满足底面△BCD为等边三角形．三个侧面△ABD，△ABC，△ACD都是等腰三角形，但AC长度不一定，三个侧面不一定全等．‎ - 9 -‎ 答案：0‎ ‎12．一个几何体的三视图如图所示，其中正视图是边长为2的正三角形，俯视图是正方形，那么该几何体的侧视图的面积是________．‎ 解析：根据三视图可知该几何体是一个四棱锥，其底面是正方形，侧棱相等，所以这是一个正四棱锥．其侧视图与正视图是完全一样的正三角形．故其面积为×22＝.‎ 答案： ‎13．如图，E，F分别为正方体的面ADD1A1，面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是________．‎ 解析：分别作出在六个面上的射影可知选②③.‎ 答案：②③‎ ‎14．[2020·洛阳高三统考]在半径为4的球面上有不同的四点A，B，C，D，若AB＝AC＝AD＝4，则平面BCD被球所截得图形的面积为________．‎ 解析：因为A，B，C，D为球面上不同的四点，所以B，C，D不共线，由AB＝AC＝AD知A在平面BCD内的射影为△BCD外接圆的圆心，记圆心为O1.设O为球的球心，则OB＝OC＝OD，故O在平面BCD内的投影也为△BCD外接圆的圆心O1，故有OA⊥平面BCD.又AB＝AC＝AD - 9 -‎ ‎＝4，所以平面BCD垂直平分线段OA.记△BCD外接圆的半径为r，由勾股定理得r2＋2＝42，即r2＝16－4＝12.从而平面BCD被球所截得的图形即△BCD的外接圆，其面积为πr2＝12π.‎ 答案：12π ‎[能力挑战]‎ ‎15．[2020·惠州调研]某三棱锥的三视图如图所示，且图中的三个三角形均为直角三角形，则xy的最大值为(　　)‎ A．32‎ B．32 C．64‎ D．64 解析：将三视图还原为如图所示的三棱锥 P－ABC，其中底面ABC是直角三角形，AB⊥BC，PA⊥平面ABC，BC＝2，PA2＋y2＝102，(2)2＋PA2＝x2，所以xy＝x＝x≤＝64，当且仅当x2＝128－x2，即x＝8时取等号，因此xy的最大值是64.选C.‎ 答案：C ‎16．如图所示是水平放置三角形的直观图，点D是△ABC的BC边中点，AB，BC分别与y′轴、x′轴平行，则三条线段AB，AD，AC中(　　)‎ - 9 -‎ A．最长的是AB，最短的是AC B．最长的是AC，最短的是AB C．最长的是AB，最短的是AD D．最长的是AC，最短的是AD 解析：由条件知，原平面图形中AB⊥BC，从而AB

查看更多