- 2021-06-05 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2019届湖南省衡阳县第三中学高二上学期期中考试(2017-11)
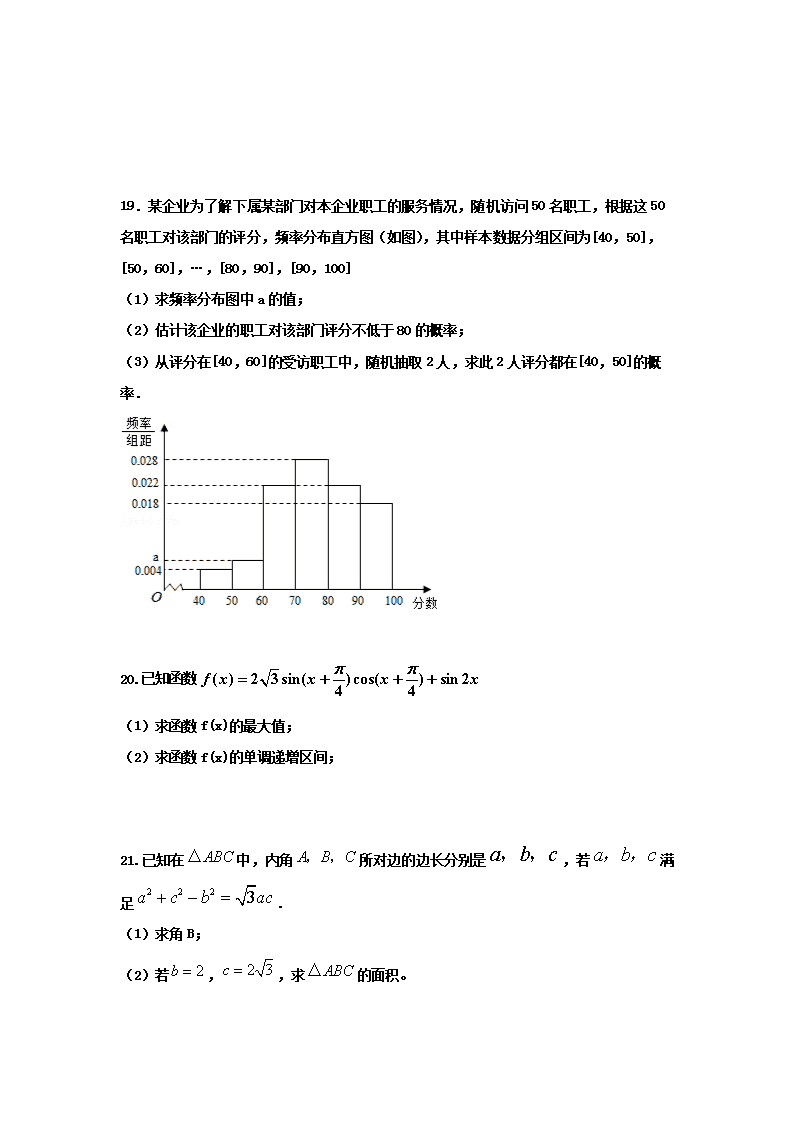
湖南省衡阳县第三中学2017-2018学年高二上学期期中考试数学(文)试题 时量120分钟,满分150分. 命题人:刘蓉琴 一、 选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合A={x|2<x<4},B={x|x<3或x>5},则A∩B=( ) A.{x|2<x<5} B.{x|x<4或x>5} C.{x|2<x<3} D.{x|x<2或x>5} 2.在中,,,,则( ) A. B. C. D. 3.与-角终边相同的角是( ) A. B. C. D. 4.已知向量a=(1,),b=(cos θ,sinθ),若a∥b,则tanθ=( ) A. B. C.- D.- 5. 若函数f=sin xcos x,x∈R,则函数f的最小值为( ) A. - B . - C. - D. -1 6.若,则下列不等式恒成立的是( ) A. B. C. D. 7.在△ABC中,若,, , 则等于 A. B.或 C. D.或 8.等差数列{an}中,S10=120,那么a1+a10的值是( ) A.12 B.24 C.36 D.48 9.在区间[1,2]上随机地取一个数X,则事件:“2x2-3x ≤ 0”发生的概率为( ) 10.在ABC中,,则这个三角形一定是( ) A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形 11.在R上定义运算⊙:,则满足的实数的取值范围为( ) A.(0,2) B.(-2,1) C. D.(-1,2) 12.在由正数组成的等比数列{an}中,若a3a4a5=,则 sin(log3a1+log3a2+....+log3a7)的值为( ) A. B. C.1 D.- 二.填空题(本大题共4小题,每小题5分,合计20分) 13.函数的最小正周期为 ; 14. f(x)为奇函数,当x<0时,f(x)=log2(1-x),则f(3)=_______. 15.若对任意的实数k,直线y-2=k(x+1)恒经过定点M,则M的 坐标是 16.数列{an}前n项和为,且,(n∈N*),则=______. 三、 说明,证明过程或演算步骤) 17.已知集合,. (1)当时,求;(2)若,求实数的取值范围. 18.如图,在正方体-中,E、F为棱AD、AB的中点. (1)求证:EF∥平面; (2)求证:平面⊥平面 19.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,频率分布直方图(如图),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] (1)求频率分布图中a的值; (2)估计该企业的职工对该部门评分不低于80的概率; (3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率. 20.已知函数 (1)求函数f(x)的最大值; (2)求函数f(x)的单调递增区间; 21.已知在中,内角所对边的边长分别是,若满足. (1)求角B; (2)若,,求的面积。 22.已知等比数列是递增数列,其前项和为,且. (1)求数列的通项公式; (2)设,求数列的前项和. 高二文科数学答案 一. 选择题: 1-5 CDCBB 6-10 DBBBA 11-12 AB 二. 填空题: 13 :π 14 :﹣2 15 :(﹣1,2) 16 :2n﹣2 三.解答题: 17.解: (1)当m=0时, B={x¦(x+1)(x-1)≥0}={x¦x≥1或x≤-1}5 A={x¦X2-2X-3˂0}={x¦-1˂X˂3} ={x¦1≤X˂3}5……………6分 (2) B={x¦ [x-(m-1)][x-(m+1)]≥0} ={x¦x≥m+1或x≤m-1} 又∵ ∴m+1≤-1或m-1≥3 即:m≤-2或m≥4………………12分 18.解:连接BD (1)在正方体-中//DB ∵E、F为棱AD、AB的中点 ∴EF//DB ∴EF// 又∵EF平面, ∴EF∥平面………………………………6分 (2)在正方体-中 ∵//DB, DB⊥AC ∴ ∴⊥平面 ∴平面⊥平面………………………12分 19:解:(1)(0.004+a+0.022+0.028+0.022+0.018)×10=1 a=0.006………………………………3分 (2) 该企业的职工对该部门评分不低于80的人数为: (0.022+0.018)×10×50=20(人) 评分不低于80的概率为:……………………3分 (3)评分在[40,50]的受访职工人数是0.004×10×50=2(人) 评分在[50,60]的受访职工人数是0.006×10×50=3(人) 分别用A1,A2; B1, B2, B3表示 {A1,A2},{A1,B1}{A1,B2}{A1,B3}{A2,B1}{A2,B2}{A2,B3}{B1,B2}{B1,B3}{B2,B3},共有10种情况,其中评分都在[40,50]只有{A1,A2}一种情况 ∴从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率是……………………………12分 20. 解:(1)f(x)=2sin(x+)cos(x+)+sin2x =sin(2x+)+sin2x =2sin(2x+) f(x)max=2 (2)当2K -≤ 2x+≤2K + (KZ)时, K -≤ x ≤ K +(KZ) 所以f(x)的单调增区间为[ K -,K +].(KZ) 21. 解:(1)则 cos B= ∴∠B=30°……………6分 ∴sin B=, 由正弦定理=, 得sin C=,∠C=60° ∵∠A+∠B+∠C=180° ,∠A=90°, S==…………………………12分 22. 解:设的公比为 , 由已知得 解得 又因为数列为递增数列 所以, ∴ .………………………………6分 (2) .………………………………12分查看更多