- 2021-06-04 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年辽宁省抚顺市第十中学高二下学期期中考试数学(理)试题(解析版)
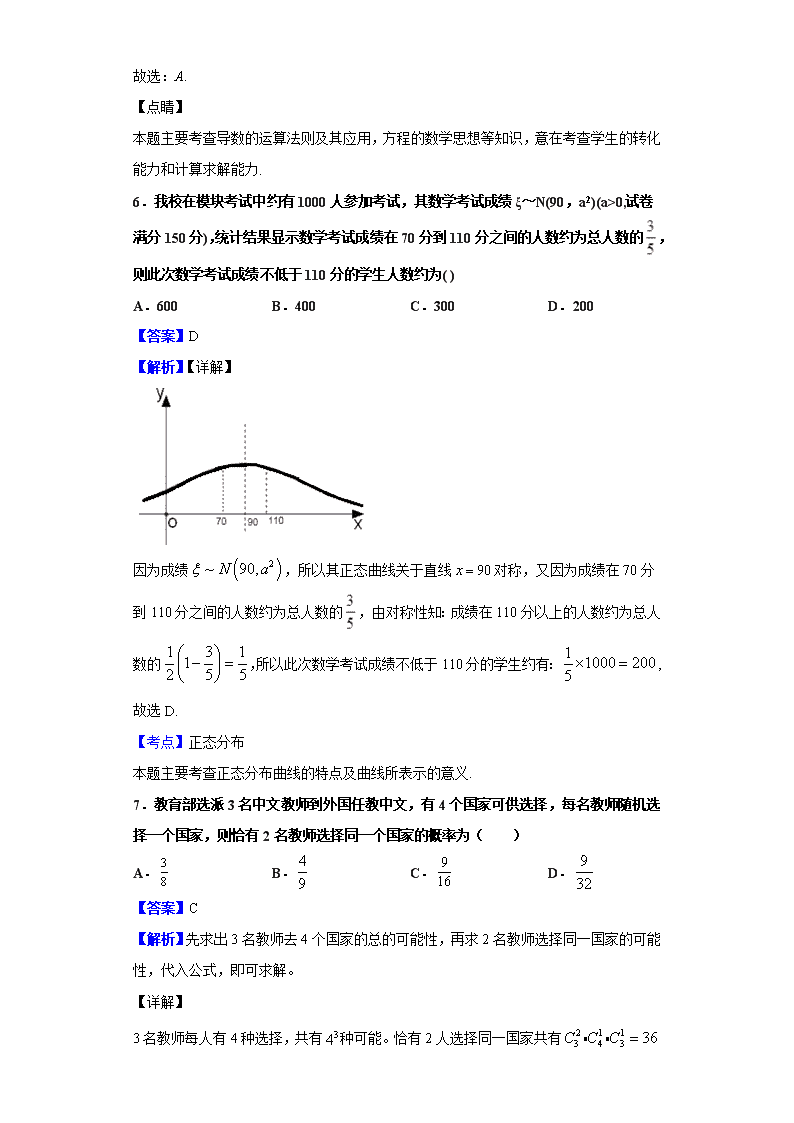
2018-2019 学年辽宁省抚顺市第十中学高二下学期期中考试 数学(理)试题 一、单选题 1.已知复数 2 3 ( )z m m mi m R 为纯虚数,则 m A. 0 B.3 C. 0 或 3 D. 4 【答案】B 【解析】因为复数 2 3z m m mi m R 为纯虚数, 2 3 0m m ,且 0m ,所 以 3m ,故选 B. 2.下列求导运算正确的是( ) A. 2 1 11x x x B. 2 1(log ) ln2x x C. 3(3 ) 3 log ex x D. 2( cos ) 2 sinx x x x 【答案】B 【解析】利用函数求导公式对选项进行一一验证. 【详解】 因为 2 1 11x x x ,故 A 错;因为 2 1(log ) ln2x x ,故 B 正确; 因为 (3 ) 3 ln3x x ,故 C 错;因为 2 2( cos ) 2 cos sinx x x x x x ,故 D 错. 【点睛】 本题考查导数公式的简单运用,考查计算能力,属于基础题. 3.用反证法证明命题:“三角形的内角中至少有一个不大于 60 度”时,反设正确的是()。 A.假设三内角都不大于 60 度; B.假设三内角至多有两个大于 60 度; C.假设三内角至多有一个大于 60 度; D.假设三内角都大于 60 度。 【答案】D 【解析】根据反证法的定义,假设是对原命题结论的否定,即可求得,得到答案. 【详解】 根据反证法的步骤可知,假设是对原命题结论的否定,“至少有一个”的否定为“一个也 没有”即“三角形三个内角都大于 60 度”,故选 D. 【点睛】 本题主要考查了反证法的概念,以及命题的否定的应用,着重考查了逻辑推理能力,属 于基础题. 4.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线:已知直线 b 平面 ,直线 a 平面 ,直线 / /b 平面 ,则直线 / /b 直线 a ”的结论显然是错误的,这 是因为( ) A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 【答案】A 【解析】分析该演绎推理的三段论,即可得到错误的原因,得到答案. 【详解】 该演绎推理的大前提是:若直线平行与平面,则该直线平行平面内所有直线, 小前提是:已知直线 / /b 平面 ,直线 a 平面 , 结论是:直线 / /b 平面 ; 该结论是错误的,因为大前提是错误的, 正确叙述是“若直线平行于平面,过该直线作平面与已知平面相交,则交线与该直线平 行”,、故选 A. 【点睛】 本题主要考查了演绎推理的三段论退,同时考查了空间中直线与平面平行的判定与性质 的应用,着重考查了推理与运算能力,属于基础题. 5.设函数 f x 的导函数为 f x ,且 2 2 1f x x xf ,则 2f =( ) A.0 B.-4 C.-2 D.2 【答案】A 【解析】由题意首先求得 ' 1f 的值,然后利用导函数的解析式可得 ' 2f 的值. 【详解】 由函数的解析式可得: ' 2 2 ' 1f x x f , 令 1x 可得: ' 1 2 2 ' 1f f ,解得: ' 1 2f , 即 ' 2 4f x x ,故 ' 2 2 2 4 0f . 故选:A. 【点睛】 本题主要考查导数的运算法则及其应用,方程的数学思想等知识,意在考查学生的转化 能力和计算求解能力. 6.我校在模块考试中约有 1000 人参加考试,其数学考试成绩ξ~N(90,a2)(a>0,试卷满 分 150 分),统计结果显示数学考试成绩在 70 分到 110 分之间的人数约为总人数的 , 则此次数学考试成绩不低于 110 分的学生人数约为( ) A.600 B.400 C.300 D.200 【答案】D 【解析】【详解】 因为成绩 2~ 90,N a ,所以其正态曲线关于直线 90x 对称,又因为成绩在 70 分 到 110 分之间的人数约为总人数的 ,由对称性知:成绩在 110 分以上的人数约为总人 数的 1 3 112 5 5 ,所以此次数学考试成绩不低于 110 分的学生约有:1 1000 2005 , 故选 D. 【考点】正态分布 本题主要考查正态分布曲线的特点及曲线所表示的意义. 7.教育部选派 3 名中文教师到外国任教中文,有 4 个国家可供选择,每名教师随机选 择一个国家,则恰有 2 名教师选择同一个国家的概率为( ) A. 3 8 B. 4 9 C. 9 16 D. 9 32 【答案】C 【解析】先求出 3 名教师去 4 个国家的总的可能性,再求 2 名教师选择同一国家的可能 性,代入公式,即可求解。 【详解】 3 名教师每人有 4 种选择,共有 34 种可能。恰有 2 人选择同一国家共有 2 1 1 3 4 3 36C C C 种可能,则所求概率 2 1 1 3 4 3 3 3 4 3 9 4 4 4 4 16 C C CP ,故选 C 【点睛】 本题考查计数原理及组合问题,考查学生分析推理,计算化简的能力,属基础题。 8.若随机变量 ~ ( 0.6)X B n, ,且 ( ) 3E X ,则 ( 1)P X 的值是( ) A. 42 0.4 B. 52 0.4 C. 43 0.4 D. 43 0.6 【答案】C 【解析】【详解】试题分析:根据随机变量符合二项分布,根据期望值求出 n 的值,写 出对应的自变量的概率的计算公式,代入自变量等于 1 时的值. 解:∵E(X)=3, ∴0.6n=3, ∴n=5 ∴P(X=1)=C51(0.6)1(0.4)4=3×0.44 故选 C. 【考点】二项分布与 n 次独立重复试验的模型. 9.将 5 名大学生分配到 3 个乡镇去任职,每个乡镇至少一名,不同的分配方案种数为 ( ) A.150 B.240 C.60 D.120 【答案】A 【解析】试题分析:分两种情况:一是按照 2,2,1 分配,有 2 2 3 5 3 3 1 902 C C A 种结果;二是 按照 3,1,1 分配,有 1 1 3 5 4 3 1 602 C C A 种结果,根据分类加法得到共90 60 150 种结果, 故选 A. 【考点】计数原理. 10.给出下面类比推理命题(其中Q为有理数集,R 为实数集,C 为复数集): ①“若 ,a bR ,则 0a b a b ”类比推出“若 a b C, ,则 0a b a b ”; ②“若 , , ,a b c d R ,则复数 ,a bi c di a c b d ”类比推出“若 , , ,a b c d Q ,则 2 2 ,a b c d a c b d ”; ③“若 ,a bR ,则 0a b a b ”类比推出“若 a b C, ,则 0a b a b ”. 其中类比结论正确的个数是( ) A. 0 B.1 C. 2 D. 3 【答案】C 【解析】因为复数不能比较大小,所以命题③是不正确的;命题①,②都是 正确的,应选答案 C。 11. 10 2 10 0 1 2 10( 2 )x a a x a x a x ,则 2 3 2 2 0 10 1 9a a a a a a ( ) A.0 B.-1 C.1 D. 10 2 1 【答案】C 【解析】由赋值法令 1x ,解得 10 0 1 2 10... 2 1a a a a , 令 1x ,解得 10 0 1 2 3 9 10... 2 1a a a a a a 再由平方差公式计算可得解. 【详解】 解:令 1x ,解得 10 0 1 2 10... 2 1a a a a , 令 1x ,解得 10 0 1 2 3 9 10... 2 1a a a a a a , 又 2 3 2 2 0 10 1 9a a a a a a =( 0 1 2 10...a a a a )( 0 1 2 3 9 10...a a a a a a ) = 10 2 1 10 2 1 =1, 故选 C. 【点睛】 本题考查了二项式定理及赋值法求展开式系数的和差,属基础题. 12.已知函数 f x 的定义域为 R ,且满足 2f x f x ,其导函数 f x , 当 1x 时, 1 1 0x f x x f x ,且 1 4f ,则不等式 1 8xf x 的解集为 ( ) A. , 2 B. 2, C. 2,2 D. , 2 2, 【答案】D 【解析】构造函数 1g x x f x , 1g x f x x f x ,当 1x 时, 1 1 0x f x x f x ,所以当 1x 时, 1 0f x x f x ,则 g x 在 , 1 上递增. 由于 2f x f x 所以函数 f x 关于点 1,0 中 心对称.所以函数 1f x 关于原点中心对称,为奇函数.令 1 1h x g x xf x , 则 h x 是 R 上的偶函数,且在 ,0 上递增,在 0, 上递 减. 2 2 2 1 2 4 8h f ,故原不等式等价于 2h x h ,等价于 2x > ,解得 2x 或 2x .故选 D . 【点睛】本小题主要考查函数单调性与奇偶性,考查函数图像的对称性的表示形式,考查 构造函数法判断函数的单调性与奇偶性.首先构造函数 1g x x f x ,利用上题 目所给含有导数的不等式可以得到函数 g x 的单调性.对于题目所给条件 2f x f x 由于 2 2x x ,所以函数图象是关于 1,0 中心对称的. 二、填空题 13.已知 1 2e a dxx ,则 41x x a 展开式中 3x 的系数为______. 【答案】32 【解析】由定积分求出实数 a 的值,再利用二项式展开式的通项公式求解即可. 【详解】 解:因为 1 2e a dxx = 2ln x e 1| =2, 由 42x 展开式的通项为 1rT = r 4C 42r rx , 即 41 2x x 展开式中 3x 的系数为 2 4C 22 + 1 4C 2 =32, 故答案为 32. 【点睛】 本题考查了二项式展开式的通项公式,属基础题. 14.已知凸 n 边形有 f n 4, Nn n 条对角线,则 1f n f n ______. 【答案】 1n 【解析】结合数学归纳法的应用即可得解. 【详解】 解:第 1n 个点与不相邻的 2n 个点有 2n 条对角线,再加上与第 1n 个点相邻的 两点有 1 条对角线,所以共增加了 1n 条对角线, 故答案为 1n . 【点睛】 本题考查了合情推理,属基础题. 15.如图是函数 y=f(x)的导函数 y=f′(x)的图象,给出下列命题: ①﹣3 是函数 y=f(x)的极值点; ②﹣1 是函数 y=f(x)的最小值点; ③y=f(x)在 x=0 处切线的斜率小于零; ④y=f(x)在区间(﹣3,1)上单调递增. 则正确命题的序号是 . 【答案】①④ 【解析】根据导函数图象可判定导函数的符号,从而确定函数的单调性,得到极值点, 以及根据导数的几何意义可知在某点处的导数即为在该点处的切线斜率. 【详解】 根据导函数图象可知当 x∈(﹣∞,﹣3)时,f'(x)<0,在 x∈(﹣3,1)时,f'(x) ≤0 ∴函数 y=f(x)在(﹣∞,﹣3)上单调递减,在(﹣3,1)上单调递增,故④正确 则﹣3 是函数 y=f(x)的极小值点,故①正确 ∵在(﹣3,1)上单调递增∴﹣1 不是函数 y=f(x)的最小值点,故②不正确; ∵函数 y=f(x)在 x=0 处的导数大于 0∴切线的斜率大于零,故③不正确 故答案为:①④ 【点睛】 本题主要考查了导函数图象与函数的性质的关系,以及函数的单调性、极值、和切线的 斜率等有关知识,属于中档题. 16.已知函数 3 2 3f x x ax x b 在 1x 处的切线平行于 x 轴,则 f x 的极 大值与极小值的差为______. 【答案】4 【解析】由导数的几何意义可得: ' ( 1) 0f ,解得 0a , 由导数的应用可得: ( ) =f x 极大值 ( 1) 2f b , ( ) =f x 极小值 (1) 2f b ,得解. 【详解】 解:因为 3 2 3f x x ax x b , 所以 ' 2( ) 3 2 3f x x ax , 由函数 3 2 3f x x ax x b 在 1x 处的切线平行于 x 轴, 所以 ' ( 1) 0f ,解得 0a , 即 ' 2( ) 3 3f x x , 当 1 1x x 或 时, ' ( ) 0f x , 1 1x 时, ' ( ) 0f x , 即函数 ( )f x 在 , 1 , 1, 为增函数,在 1,1 为减函数, 所以 ( ) =f x 极大值 ( 1) 2f b , ( ) =f x 极小值 (1) 2f b , 故 f x 的极大值与极小值的差为 2 2 4b b , 故答案为 4. 【点睛】 本题考查了利用导数求函数的极值,属中档题. 三、解答题 17.已知 . (1)如果 ,求 的值; (2)如果 ,求实数 的值. 【答案】(1) (2) 【解析】试题分析:(1)本问考查共轭复数,复数的乘方,由 , ,于是 可以经过计算求出 ;(2)本问考查复数除法运算及两个复数相等的充要条件, ( ), ( ),则 的充要条件是 且 ,列方程组可以求 解. 试题解析:(1)∵ , ∴ . (2)∵ , ∴ . ∴ ,解得 . 18.已知函数 lnf x x x . (Ⅰ)求 f x 的最小值; (Ⅱ)若对所有 1x 都有 1f x ax ,求实数 a 的取值范围. 【答案】(Ⅰ)最小值 1 e ;(Ⅱ) ,1 【解析】(Ⅰ)由导数的应用,研究函数的单调性,再求其最值, (Ⅱ)构造函数 1lng x x x ,由导数的应用求函数的最值即可得解. 【详解】 解:(Ⅰ) f x 的定义域为 0, , f x 的导数 1 lnf x x . 令 0f x , 解得 1 ex ;令 0f x ,解得 10 ex .从而 f x 在 10, e 单调递减,在 1 ,e 单调递增. 所以,当 1 ex 时, f x 取得最小值 1 e . (Ⅱ)依题意,得 1f x ax 在 1, 上恒成立,即不等式 1lna x x 对于 1,x 恒成立. 令 1lng x x x , 则 2 1 1 1 11g x x x x x . 当 1x 时,因为 1 11 0g x x x , 故 g x 是 1, 上的增函数,所以 g x 的最小值是 1 1g , 从而 a 的取值范围是 ,1 . 【点睛】 本题考查了利用导数求函数的最值及利用导数研究不等式,属中档题. 19.“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号. 某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价, 将该产品按事先拟定的价格进行试销,得到一组销售数据 ,i ix y 1,2, ,6i ,如表 所示: 试销单价 x (元) 4 5 6 7 8 9 产品销量 y (件) q 84 83 80 75 68 已知 6 1 1 806 i i y y , 6 1 3050i i i x y . (Ⅰ)求出 q的值; (Ⅱ)已知变量 x , y 具有线性相关关系,求产品销量 y (件)关于试销单价 x (元) 的线性回归方程 ˆˆ ˆy bx a ; (Ⅲ)用 iy 表示用(Ⅱ)中所求的线性回归方程得到的与 ix 对应的产品销量的估计值. 当销售数据 ,i ix y 对应的残差的绝对值 1iiy y 时,则将销售数据 ,i ix y 称为一个 “好数据”.现从 6 个销售数据中任取 2 个,求“好数据”至少有一个的概率. (参考公式:线性回归方程中b , a 的最小二乘估计分别为 1 2 2 1 ˆ n i i i n i i x y nxy b x nx , ˆˆa y bx ) 【答案】(Ⅰ) 90q ;(Ⅱ) ˆ 4 106y x ;(Ⅲ) 4 5P A 【解析】(Ⅰ)利用平均数求出 90q 即可; (Ⅱ)参考公式求解线性回归方程即可得解; (Ⅲ)结合(Ⅱ),满足 1iiy y 1,2, ,6i 的共有 3 个“好数据”,又从 6 个销售 数据中任取 2 个,共有15 种不同的取法,利用概率公式运算即可. 【详解】 (Ⅰ) 6 1 1 806 i i y y ,可求得 90q . (Ⅱ) 6 1 6 2 2 1 3050 6 6.5 80 70ˆ 4271 253.5 17.5( ) i i i i i x y nxy b x n x , ˆˆ 80 4 6.5 106a y bx , 所以所求的线性回归方程为 ˆ 4 106y x . (Ⅲ)利用(Ⅱ)中所求的线性回归方程 ˆ 4 106y x 可得,当 1 4x 时, 1 90y ; 当 2 5x 时, 2 86y ;当 3 6x 时, 3 82y ;当 4 7x 时, 4 78y ;当 5 8x 时, 5 74y ;当 6 9x 时, 6 70y . 与销售数据对比可知满足 1iiy y 1,2, ,6i 的共有 3 个“好数据”: 4,90 、 6,83 、 8,75 . 又从 6 个销售数据中任取 2 个,共有 2 6C =15 种不同的取法, 设所求事件用 A 表示 ,则 3 41 1 15 5P A P A . 【点睛】 本题考查了回归直线及概率公式,属中档题. 20.为了解七班学生喜爱打篮球是否与性别有关,对本班 50 人进行了问卷调查得到了 如下的列联表: 喜爱打篮球 不喜爱打篮球 合 男生 5 女生 10 合计 50 已知在全部 50 人中随机抽取 1 人抽到喜爱打篮球的学生的概率为 3 5 . (1)请将上面的列联表补充完整(不用写计算过程); (2)能否在犯错误的概率不超过 0.005 的前提下认为喜爱打篮球与性别有关?说明你 的理由; (3)现从女生中抽取 2 人进一步调查,设其中喜爱打篮球的女生人数为 ,求 的分 布列与期望. 下面的临界值表供参考: 2 0( )P K k 0.15 0.10 0.05[ 0.025 0.01 0.005 0.001 0k 2.072 2.70 3.841 5.024 6.635 7.879 10.82 (参考公式: 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d ,其中 n a b c d ) 【答案】(1)见解析(2)能(3) 3 20 【解析】解:(1) 列联表补充如下:- 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50 (2)∵ ∴在犯错误的概率不超过 0.005 的前提下,认为喜爱打篮球与性别有关. (3)喜爱打篮球的女生人数 的可能取值为 . 其概率分别为 , , 故 的分布列为: 的期望值为: 【详解】 本题是一个统计综合题,包含独立性检验、离散型随机变量的期望与方差和概率,本题 通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度. (1)根据在全部 50 人中随机抽取 1 人抽到喜爱打篮球的学生的概率,做出喜爱打篮球 的人数,进而做出男生的人数,填好表格. (2)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看 出有多大的把握说明打篮球和性别有关系. (3)喜爱打篮球的女生人数ξ的可能取值为 0,1,2,通过列举得到事件数,分别计算 出它们的概率,最后利用列出分布列,求出期望即可. 解:(1) 列联表补充如下:----------------------------------------3 分 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50 (2)∵ 2 2 50 (20 15 10 5) 8.333 7.87930 20 25 25K ------------------------6 分 ∴在犯错误的概率不超过 0.005 的前提下,认为喜爱打篮球与性别有 关.---------------------7 分 (3)喜爱打篮球的女生人数 的可能取值为 0,1,2 .-------------------------9 分 其概率分别为 0 2 10 15 2 25 7( 0) 20 C CP C , 1 1 10 15 2 25 1( 1) 2 C CP C , 2 0 10 15 2 25 3( 2) 20 C CP C --------------------------12 分 故 的分布列为: 0 1 2 P 7 20 1 2 3 20 --------------------------13 分 的期望值为: 7 1 3 40 1 220 2 20 5E ---------------------14 分 21.已知数列 na 的前 n 项和为 nS ,且 1 1a , 2 * n nS n a n N . (1)试求 S1,S2,S3,S4,并猜想 Sn 的表达式; (2)证明你的猜想. 【答案】(1) 1 1S , 2 4 3S , 3 6 4S , 4 8 5S ,猜想 2 1n nS n ;(2)见解析 【解析】(1)由不完全归纳法可得: 2 1n nS n ; (2)利用数学归纳法,先假设当 n k 时,猜测正确,再证明当 1n k 时,命题成 立即可. 【详解】 (1)∵ 1 1a , 2 * n nS n a n N . ∴ 1 1 1S a , 2 2 21 4S a a , 2 1 3a ,∴ 2 1 2 1 41 3 3S S a ; 3 2 3 39S S a a , 3 1 6a ,∴ 3 2 3 4 1 9 3 6 3 6 6 2 4S S a ; 4 3 4 416S S a a , 4 1 10a ,∴ 4 3 4 3 1 16 8 2 10 10 5S S a ; ∴ 1 21 2S , 2 4 3S , 3 6 4S , 4 8 5S 猜测: 2 1n nS n . (2)用数学归纳法证明如下: ①当 1n 时,猜测显然正确. ②假设当 n k 时,猜测正确,即 2 1k kS k 则当 1n k 时, 由 2 22 2 1 1k k k k kS k a k a ak k k 2 2 1 1 1 1 1 21 11k k k k k k kS S a k a a k ak 1 2 1 2ka k k ∴ 1 1 2 1 2 12 2 1 1 2 2 1 1k k k k kkS S a k k k k k . 这就是说,当 1n k 时,猜测也是正确的. 由①、②知,对一切 *n nN 都有 2 1n nS n . 【点睛】 本题考查了不完全归纳法及数学归纳法,属中档题. 22.已知函数 211 2 xf x x e ax a R . (1)讨论函数 f x 的单调性; (2)当函数 f x 有两个零点,求实数 a 的取值范围. 【答案】(1)答案见解析;(2) ,0 . 【解析】分析:(1)先求导,再对 a 分类讨论,求函数的单调区间. (2)对 a 分类讨论, 作出函数的图像,分析出函数 f(x)有两个零点所满足的条件,从而求出 a 的取值范围. 详解:(1)由题意得 xf x x e a ①当 0a 时,令 0f x ,则 0x ; 令 0f x ,则 0x , ∴ f x 在 ,0 上单调递减,在 0, 上单调递增; ②当 0a 时,令 0f x ,则 0x 或 lnx a , (ⅰ)当 0 1a 时,令 0f x ,则 lnx a 或 0x ; 令 0f x ,则 ln 0a x , ∴ f x 在 ,lna 和 0, 上单调递增,在 ln ,0a 上单调递减; (ⅱ)当 1a 时, 1 0xf x x e , ∴ f x 在 R 上单调递增; (ⅲ)当 1a 时,令 0f x ,则 0x 或 lnx a ; 令 0f x ,则 0 lnx a , ∴ f x 在 ,0 和 ln ,a 上单调递增,在 0,lna 上单调递减; (2)由(1)得当 0 1a 时, f x 在 ,lna 和 0, 上单调递增,在 ln ,0a 上单调递减, ∴ f x 在 lnx a 处取得极大值 lnf a , ∵ 221 1ln ln 1 ln ln 1 1 02 2f a a a a a a a , ∴此时不符合题意; 当 1a 时, f x 在 R 上单调递增, ∴此时不符合题意; 当 1a 时, f x 在 ,0 和 ln ,a 上单调递增,在 0,lna 上单调递减; ∴ f x 的 0x 处取得极大值 0f , ∵ 0 1 0f , ∴此时不符合题意; 当 0a 时, f x 在 ,0 上单调递减,在 0, 上单调递增, ∵ 0 1 0f , 11 02f a , ∴ f x 在 0, 上有一个零点, (ⅰ)当 0a 时,令 0 min ln , 1 3x a ,当 0x x 时, ∵ 2 2 21 1 11 1 2 2 02 2 2 xf x x e ax a x ax a x x , ∴ f x 在 ,0 上有一个零点, ∴此时符合题意; (ⅱ)当 0a 时,当 0x 时, 1 0xf x x e , ∴ f x 在 ,0 上没有零点,此时不符合题意; 综上所述,实数 a 的取值范围为 ,0 . 点睛:对于含参的问题,注意分类讨论思想的运用. 本题的导数 xf x x e a ,由于无法直接写出函数的单调区间,所以必须要分类讨论. 分类讨论时,要注意分类的起因、分类的标准、分类的过程和分类的结论.查看更多