北师大版九年级数学（下册）第三章圆

北师大版九年级数学（下册）第三章圆

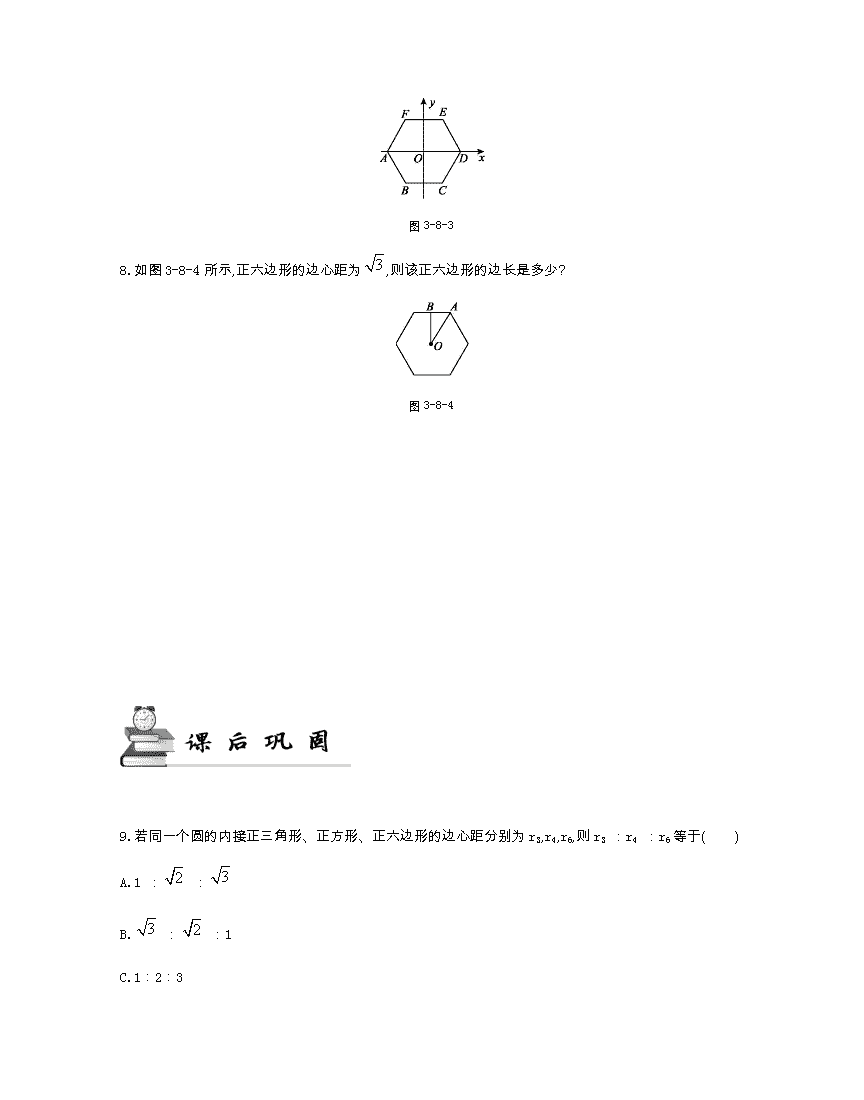
北师大版九年级数学（下册）‎ 第三章 圆 ‎3.7切线长定理 课时练习 ‎1.如图3-8-1所示,六边形ABCDEF是圆O的　　　　　,圆O叫做这个正六边形的　　　　　;OB是这个正六边形的　　　　　; 　　　　　是这个正六边形的中心角;OP⊥BC,垂足为P,OP是这个正六边形的　　　　　.‎ 图3-8-1‎ ‎2.用尺规作出圆内接正四边形.‎ ‎3.如图3-8-2所示,☉O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是(　　)‎ 图3-8-2‎ A.72°‎ B.60°‎ C.54°‎ D.36°‎ ‎4.一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是(　　)‎ A.2‎ B.‎ C.1‎ D.‎ ‎5.已知圆的半径是2,则该圆的内接正六边形的面积是(　　)‎ A.3‎ B.9‎ C.18‎ D.36‎ ‎6.已知圆内接正六边形的边长是1,则这个圆的内接正方形的边长是　　　　　.‎ ‎7.如图3-8-3所示,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-1,0),则点C的坐标为　　　　　.‎ 图3-8-3‎ ‎8.如图3-8-4所示,正六边形的边心距为,则该正六边形的边长是多少?‎ 图3-8-4‎ ‎9.若同一个圆的内接正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3 ：r4 ：r6等于(　　)‎ A.1 ： ：‎ B. ： ：1‎ C.1：2：3‎ D.3：2：1‎ ‎10.如图3-8-5所示,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为(　　)‎ 图3-8-5‎ A.20‎ B.40‎ C.60‎ D.80‎ ‎11.如图3-8-6所示,在正五边形ABCDE中,连接AC,AD,则∠CAD的度数是　　　　　度.‎ 图3-8-6‎ ‎12.如图3-8-7所示,五边形ABCDE是正五边形,有一点P,满足两个条件：△BCD与△PCD的面积相等,且△ABP是等腰三角形,则以下四个命题正确的是　　　　　.‎ 图3-8-7‎ ‎①当点P在正五边形ABCDE的内部时,满足条件的点P有三个;‎ ‎②当点P在正五边形ABCDE的边上时,点P与点E重合;‎ ‎③当点P在正五边形ABCDE的外部时,满足条件的点P只有一个;‎ ‎④在正五边形ABCDE的平面内,满足条件的点P有五个.‎ ‎13.如图3-8-8所示,△ABC是☉O的内接等腰三角形,顶角∠BAC=36°,弦BD,CE分别平分∠ABC,∠ACB.‎ 求证：五边形AEBCD是正五边形.‎ 图3-8-8‎ 参考答案 ‎1.内接正六边形　　　中心　　　半径　　　∠BOC　　　边心距 ‎2.解：作图如图所示, ‎ 作法如下：‎ ‎(1)任意作圆O的互相垂直的两条直径,在圆周上得到四个点.‎ ‎(2)依次连接这四个点,就得到这个圆的一个内接正四边形.‎ ‎3.A ‎4.A ‎5.C ‎6.‎ ‎7.‎ ‎8.解：∵正六边形的边心距为,‎ ‎∴OB=,AB=OA.‎ ‎∵OA2=AB2+OB2,‎ ‎∴OA2=+,‎ 解得OA=2.‎ ‎9.A ‎10.B ‎11.36‎ ‎12.②④‎ ‎13.证明：∵△ABC为等腰三角形,顶角∠BAC=36°,‎ ‎∴∠ABC=∠ACB=72°.‎ 又∵BD,CE分别平分∠ABC,∠ACB,‎ ‎∴∠ABD=∠CBD=∠ACE=∠BCE=∠BAC =36°,‎ ‎∴AD=CD=AE=BE=BC,‎ ‎∴五边形AEBCD是正五边形.‎