- 2021-06-03 发布 |
- 37.5 KB |
- 45页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学选修2-3教学课件:7_1分类分步原理
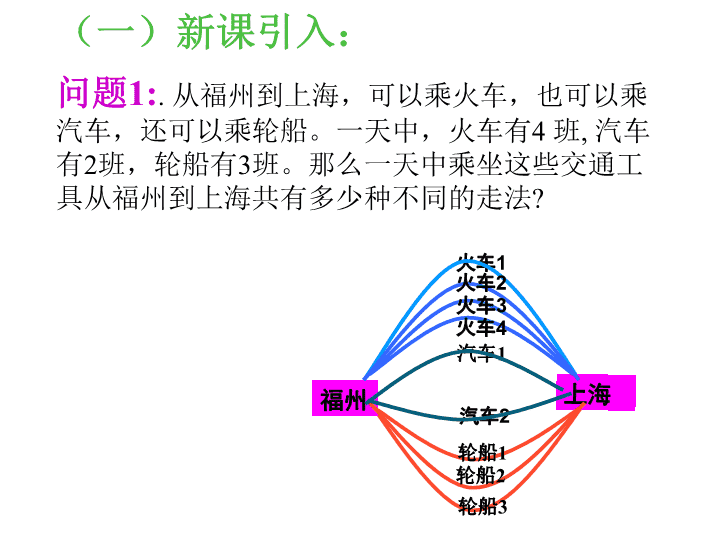
分类计数原理和分步计数原理 问题 1: . 从福州到上海,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有 4 班 , 汽车有 2 班,轮船有 3 班。那么一天中乘坐这些交通工具从福州到上海共有多少种不同的走法 ? (一)新课引入: 火车 1 轮船 3 福州 上海 汽车 1 汽车 2 火车 2 火车 3 火车 4 轮船 2 轮船 1 问题 1: . 从福州到上海,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有 4 班 , 汽车有 2 班,轮船有 3 班。那么一天中乘坐这些交通工具从福州到上海共有多少种不同的走法 ? 分析 : 从福州到上海有 3 类方法 , 第一类方法 , 乘火车,有 4 种方法 ; 第二类方法 , 乘汽车,有 2 种方法 ; 第三类方法 , 乘轮船 , 有 3 种方法 ; 所以 从福州到上海共有 4 + 2 + 3 = 9 种方法。 (一)新课引入: 问题 2: 如图 , 由 A 村去 B 村的道路有 3 条,由 B 村去 C 村的道路有 2 条。从 A 村经 B 村去 C 村,共有多少种不同的走法 ? A 村 B 村 C 村 北 南 中 北 南 问题 2: 如图 , 由 A 村去 B 村的道路有 3 条,由 B 村去 C 村的道路有 2 条。从 A 村经 B 村去 C 村,共有多少种不同的走法 ? A 村 B 村 C 村 北 南 中 北 南 分析 : 从 A 村经 B 村去 C 村有 2 步 , 第一步 , 由 A 村去 B 村有 3 种方法 , 第二步 , 由 B 村去 C 村有 2 种方法 , 所以 从 A 村经 B 村去 C 村共有 3 ×2 = 6 种不同的方法。 分类记数原理 : 做一件事情,完成它可以有 n 类办法 , 在第一类办法中有 m 1 种不同的方法 , 在第二类办法中有 m 2 种不同的方法, …… ,在第 n 类办法中有 m n 种不同的方法。那么完成这件事共有 N=m 1 +m 2 +…+m n 种不同的方法。 分步记数原理: 做一件事情,完成它需要分成 n 个步骤,做第一步有 m 1 种不同的方法,做第二步有 m 2 种不同的方法, …… ,做第 n 步有 m n 种不同的方法,那么完成这件事有 N=m 1 ×m 2 ×…×m n 种不同的方法 。 (二)新课: 分类计数原理与分步计数原理,回答的都是有关完成一件事情的不同方法种数的问题。 当每种方法可以独立完成的用分类计数原理,将各方法数相加;当完成一件事情需要分为几步,则应用分步计数原理,将每步方法数相乘。 原理(名称) 针对的问 题类型 各种方法之间点的关系 其中任意一种 方法的效果 分类计数原理 分类 相互独立 完成 分步计数原理 分步 相互依存 完不成 反思辨析 (2) 从书架的第 1 、 2 、 3 层各取一本书 , 有多少种不同的取法 ? (2) 24 种 ( 分析 : 用分步计数原理: 4×3×2=24 种 ) 例 1 :书架的第一层放有 4 本不同的计算机书 , 第二层放有 3 本不同的文艺书 , 第 3 层放有 2 本不同的体育书 . (1) 从书架上任取 1 本书 , 有多少种不同的取法 ? (1) 9 种 ( 分析 : 从第一层取有 4 种 , 从第二层取有 3 种,从第三层取有 2 种,用分类计数原理 4+3+2=9 种 ) (三)例题: 例 3. 一种号码锁有 4 个拨号盘,每个拨号盘上有从 0 到 9 共十个数字 , 这 4 个拨号盘可以组成多少个四位数的号码 ( 各位上的数字允许重复 ) ?首位数字不为 0 的号码数是多少?首位数字是 0 的号码数又是多少? 分析 : 按号码位数 , 从左到右依次设置第一位、第二位、第三 位 , 第四位、需分为 四步完成 ; 第一步 , m 1 = 10; 第二步 , m 2 = 10; 第三步 , m 2 = 10 ,第 四步 , m 4 = 10. 根据 分步记数原理 , 共可以设置 N = 10×10×10 ×10 = 10 4 种四位数的号码。 答 : 首位数字不为 0 的号码数是 N =9×10×10 ×10 = 9×10 3 种 , 首位数字是 0 的号码数是 N = 1×10×10 ×10 = 10 3 种。 由此可以看出 , 首位数字不为 0 的号码数与首位数字是 0 的号 码数之和等于号码总数。 例 3. 一种号码锁有 4 个拨号盘,每个拨号盘上有从 0 到 9 共十个数字 , 这 4 个拨号盘可以组成多少个四位数的号码 ( 各位上的数字允许重复 ) ?首位数字不为 0 的号码数是多少?首位数字是 0 的号码数又是多少? 问 : 若设置四个、五个、六个、 … 、号码盘 , 号码数分别有多少种? 答 : 它们的号码种数依次是 10 4 , 10 5 , 10 6 , …… 种。 点评 : 分类记数原理 中的“分类”要全面 , 不能遗漏 ; 但也不能重复、交叉 ;“ 类”与“类之间是并列的、互斥的、独立的 , 也就是说 , 完成一件事情 , 每次只能选择其中的一类办法中的某一种方法。若完成某件事情有 n 类办法 , 即它们两两的交为空集 ,n 类的并为全集。 分步记数原理 中的“分步”程序要正确。“步”与“步”之间是连续的 , 不间 断的 , 缺一不可 ; 但也不能重复、交叉 ; 若完成某件事情需 n 步 , 则必须且只需依次完成这 n 个步骤后 , 这件事情才算完成。 在运用“ 分类记数原理 、 分步记数原理 ”处理具体应用题时 , 除要弄清是“分类”还是“分步”外 , 还要搞清楚“分类”或“分步”的具体标准。在“分类”或“分步”过程中 , 标准必须一致 , 才能保证不重复、不遗漏。 A U C C U U A A A G G ㈣ 课堂练习 1 . 如图 , 要给地图 A 、 B 、 C 、 D 四个区域分别涂上 3 种不同颜色中的某一种 , 允许同一种颜色使用多次 , 但相邻区域必须涂不同的颜色 , 不同的涂色方案有多少种? 解 : 按地图 A 、 B 、 C 、 D 四个区域依次分四步完成 , 第一步 , m 1 = 3 种 , 第二步 , m 2 = 2 种 , 第三步 , m 3 = 1 种 , 第四步 , m 4 = 1 种 , 所以根据 分步记数原理 , 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。 ㈣ 课堂练习 1 . 如图 , 要给地图 A 、 B 、 C 、 D 四个区域分别涂上 3 种不同颜色中的某一种 , 允许同一种颜色使用多次 , 但相邻区域必须涂不同的颜色 , 不同的涂色方案有多少种? 问 : 若用 2 色、 3 色、 4 色、 5 色等 , 结果又怎样呢? 答 : 它们的涂色方案种数分别是 0, 3×2×1×1=6 4×3×2×2 = 48, 5×4×3×3 = 180 种等。 3 . 如图 , 该电路 , 从 A 到 B 共有多少条不同的线路可通电? A B 课堂练习 2 所以 , 根据分类原理 , 从 A 到 B 共有 N = 3 + 1 + 4 = 8 条不同的线路可通电。 在解题有时既要分类又要分步。 解 : 从总体上看由 A 到 B 的通电线路可分三类 , 第一类 , m 1 = 3 条 第二类 , m 2 = 1 条 第三类 , m 3 = 2×2 = 4, 条 练习 3. 如图 , 从甲地到乙地有 2 条路可通 , 从乙地到丙地有 3 条路可通 ; 从甲地到丁地有 4 条路可通 , 从丁地到丙地有 2 条路可通。从甲地到丙地共有多少种不同的走法? 甲地 乙地 丙地 丁地 解 : 从总体上看 , 由甲到丙有两类不同的走法 , 第一类 , 由甲经乙去丙 , 又需分两步 , 所以 m 1 = 2×3 = 6 种不同的走法 ; 第二类 , 由甲经丁去丙 , 也需分两步 , 所以 m 2 = 4×2 = 8 种不同的走法 ; 所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。 4 . 如图 , 一蚂蚁沿着长方体的棱 , 从的一个顶点爬到相对的另一个顶点的最近路线共有多少条? 解 : 如图 , 从总体上看 , 如 , 蚂蚁从顶点 A 爬到顶点 C 1 有三类方法 , 从局部上看每类又需两步完成 , 所以 , 第一类 , m 1 = 1×2 = 2 条 第二类 , m 2 = 1×2 = 2 条 第三类 , m 3 = 1×2 = 2 条 所以 , 根据 分类记数原理 , 从顶点 A 到顶点 C 1 最近路线共有 N = 2 + 2 + 2 = 6 条。 5. 现要安排一份 5 天值班表,每天有一个人值班。共有 5 个人,每个人都可以值多天班或不值班,但相邻两天不能由同一个人值班,问此值班表由多少种不同的排法? 解:分 5 步进行: 第一步:先排第一天,可排 5 人中的任一个,有 5 种排法; 第二步:再排第二天,此时不能排第一天的人,有 4 种排法 ; 第三步:再排第三天,此时不能排第二天的人,有 4 种排法 ; 第四步:同前 第五步:同前 由分步计数原理可得不同排法有 5×4×4×4×4 = 1280 种 6. ①用 0 , 1 , 2 , …… , 9 可以组成多少个 8 位号码; ②用 0 , 1 , 2 , …… , 9 可以组成多少个 8 位整数; ③用 0 , 1 , 2 , …… , 9 可以组成多少个无重复数字的 4 位整数; ④用 0 , 1 , 2 , …… , 9 可以组成多少个有重复数字的 4 位整数; ⑤用 0 , 1 , 2 , …… , 9 可以组成多少个无重复数字的 4 位奇数; 10×10×10×10×10×10×10×10 = 10 8 9×10×10×10×10×10×10×10 = 9×10 7 9×9×8×7 = 4536 9×10×10×10 = 9000 先定个位,再定千位,最后定百、十位 5×8×8×7 = 2240 7 . 5 张 1 元币, 4 张 1 角币, 1 张 5 分币, 2 张 2 分币, 可组成多少种不同的币值?( 1 张不取,即 0 元 0 分 0 角不计在内) 元: 0 , 1 , 2 , 3 , 4 , 5 角: 0 , 1 , 2 , 3 , 4 分: 0 , 2 , 4 , 5 , 7 , 9 6×5×6 - 1 = 179 ㈤ 小结: 1. 本节课学习了那些主要内容? 答 : 分类记数原理 和 分步记数原理 。 2 . 分类记数原理 和 分步记数原理 的共同点是什么? 不同点什么? 答 : 共同点是 , 它们都是研究完成一件事情 , 共有多少种不 同的方法。 不同点是 , 它们研究完成一件事情的方式不同 , 分类记 数原理 是“分类完成” , 即任何一类办法中的任何一个方法都能完成这件事。 分步记数原理 是“分步完成” , 即这些方法需要分步 , 各个步骤顺次相依 , 且每一步都完成了 , 才能完成这件事情。这也是本节课的重点。 3. 何时用 分类记数原理 、 分步记数原理 呢 ? 答 : 完成一件事情有 n 类方法 , 若每一类方法中的任何一种方法均能将这件事情从头至尾完成 , 则计算完成这件事情的方法总数用 分类记数原理 。 完成一件事情有 n 个步骤 , 若每一步的任何一种方法只能完成这件事的一部分 , 并且必须且只需完成互相独立的这 n 步后 , 才能完成这件事 , 则计算完成这件事的方法总数用 分步记数原理 。 ㈤ 小结: 练习: 三个比赛项目,六人报名参加。 1)每人参加一项有多少种不同的方法? 2)每项1人,且每人至多参加一项,有多少种不同的方法? 3)每项1人,每人参加的项数不限,有多少种不同的方法? 例 1 、将数字 1,2,3,4, 填入标号为 1,2,3,4 的四个方格里 , 每格填一个数字 , 则每个格子的标号与所填的数字均不同的填法有 _____ 种 拓展引申 : 1号方格里可填2,3,4三个数字,有3种填法。1号方格填好后,再填与1号方格内数字相同的号的方格,又有3种填法,其余两个方格只有1种填法。 所以共有 3*3*1=9 种不同的方法。 二、映射个数问题 : 例 2 设 A={a,b,c,d,e,f},B={x,y,z}, 从 A 到 B 共有多少种不同的映射 ? 三、染色问题 : 例 3. 如图 , 用 5 种不同颜色给图中的 A 、 B 、 C 、 D 四个区域涂色 , 规定一个区域 只涂一种颜色 , 相邻区域必须涂不同的颜色 , 不同的涂色方案有 种。 A B C D 分析: 如图, A 、 B 、 C 三个区域两两相邻, A 与 D 不相邻,因此 A 、 B 、 C 三个区域的颜色两两不同, A 、 D 两个区域可以同色,也可以不同色,但 D 与 B 、 C 不同色。由此可见我们需根据 A 与 D 同色与不同色分成两大类。 解: 先分成两类:第一类, D 与 A 不同色,可分成四步完成。 第一步涂 A 有 5 种方法,第二步涂 B 有 4 种方法;第三步涂 C 有 3 种方法;第四步涂 D 有 2 种方法。根据分步计数原理, 共有 5 ×4×3×2 = 120 种方法。 根据分类计数原理,共有 12 0+60 = 180 种方法。 第二类, A 、 D 同色,分三步完成, 第一步涂 A 和 D 有 5 种方法,第二步涂 B 有 4 种方法;第三步涂 C 有 3 种方法。根据分步计数原理,共有 5 ×4×3 = 60 种方法。 例 4 、某城市在中心广场建造一个花圃,花圃分为 6 个部分(如右图)现要栽种 4 种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ______ 种 . (以数字作答) ( 1 )②与⑤同色,则③⑥也同色或④⑥也同色,所以共有 N 1 =4×3×2×2×1=48 种; 所以,共有 N = N 1 + N 2 + N 3 =48+48+24=120 种 . ( 2 ) ③与⑤同色,则②④或⑥④同色,所以共有 N 2 =4×3×2×2×1=48 种; ( 3 ) ②与④且③与⑥同色,则共 N 3 =4×3×2×1=24 种 解法一:从题意来看 6 部分种 4 种颜色的花,又从图形看 知必有 2 组同颜色的花,从同颜色的花入手分类求 例 6 、将3种作物种植在如图所示的5块试验田里,每块种植一种作物且相邻的试验田不能种植同一种作物,不同的种植方法共有 种(以数字作答) 42 例 5 、如图,是 4 个相同的正方形,用红、黄、蓝、白 4 种颜色涂这些正方形,使每个正方形涂一种颜色,那么共有多少种涂色方法? 四、子集问题 规律: n 元集合 的不同子集有个 。 例 7 : 集合 A={a,b,c,d,e}, 它的子集个数为 ,真子集个数为 ,非空子集个数为 ,非空真子集个数为 。 五、综合问题 : 例 8 若直线方程 ax+by=0 中的 a,b 可以从 0,1,2,3,4 这五个数字中任取两个不同的数字 , 则方程所表示的不同的直线共有多少条 ? 例 9 : 在所有的两位数中,个位数字比十位数字大的两位数有多少个? 分析与解:分析个位数字,可分以下几类. 个位是 9 ,则十位可以是 1 , 2 , 3… , 8 中的一个,故有 8 个; 个位是 8 ,则十位可以是 1 , 2 , 3… , 7 中的一个,故有 7 个; 与上同样: 个位是 7 的有 6 个; 个位是 6 的有 5 个; …… 个位是 2 的只有 1 个. 由分类计数原理知,满足条件的两位数有 说明:本题是用分类计数原理解答的,结合本题可加深对“做一件事,完成之可以有 n 类办法”的理解,所谓“做一件事,完成它可以有 n 类办法”,这里是指对完成这件事情的所有办法的一个分类.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次分类时要注意满足一个基本要求: 完成这件事的任何一种方法必须属于某一类,并且分别属于不同两类的两种方法是不同的方法, 只有满足这些条件,才可以用分类计数原理. 综合应用 例 10 .有不同的中文书 9 本,不同的英文书 7 本,不同的日文书 5 本.从其中取出不是同一国文字的书 2 本,问有多少种不同的取法? 例 11 .集合 A={1,2,-3},B={-1,-2,3,4} .从 A,B 中各取 1 个元素作为点 P(x,y) 的坐标. ( 1 )可以得到多少个不同的点? ( 2 )这些点中,位于第一象限的有几个? (3)这些点中,有多少个不落在直线 y=-x 上? 9×7 + 9×5 + 7×5 = 143 3×4 + 4×3 = 24 2×2 + 2×2 = 8 2 4-6=1 8 例 12 、 75600 有多少个正约数 ? 有多少个奇约数 ? 解 : 由于 75600=2 4 ×3 3 ×5 2 ×7 75600 的每个约数都可以写成 的形式 , 其中 , , , 于是 , 要确定 75600 的一个约数 , 可分四步完成 , 即 i,j,k,l 分别在各自的范围内任取一个值 , 这样 i 有 5 种取法 ,j 有 4 种取法 ,k 有 3 种取法 ,l 有 2 种取法 , 根据分步计数原理得约数的个数为 5×4×3×2=120 个 . 例 13 、如果把两条异面直线看成“一对”,那么六棱锥的棱所在的 12 条直线中,异面直线共有( )对 A.12 B.24 C.36 D.48 B 1 、3个班分别从5个风景点中选择一处游览,不同选法的种数是3 5 还是5 3 ? 2 、乘积( a 1 +a 2 +a 3 )( b 1 +b 2 +b 3 +b 4 )( c 1 +c 2 +c 3 +c 4 +c 5 ) 展开后共有多少项? 3 、设集合 A={1 , 2 , 3 , 4},B={5 , 6 , 7} ,则以 A 到 B 的所有不同映射共有多少个? 4 、已知集合 M={-3 , -2 , -1 , 0 , 1 , 2}a,b∈M ,平面直角坐标系内点 P 的坐标是( a,b ) ① P 可以表示多少个不同的点? ② P 可以表示多少个坐标轴上的点? ③ P 可以表示第二象限内的点吗? ④ P 可以表示直线 y=x 上的点吗? 两大原理妙无穷 , 茫茫数理此中求。 万万千千说不尽 , 运用解题任驰骋 。 两个基本原理的课外练习查看更多