2019八年级数学上册 第14章 勾股定理 14直角三角形三边的关系

2019八年级数学上册 第14章 勾股定理 14直角三角形三边的关系

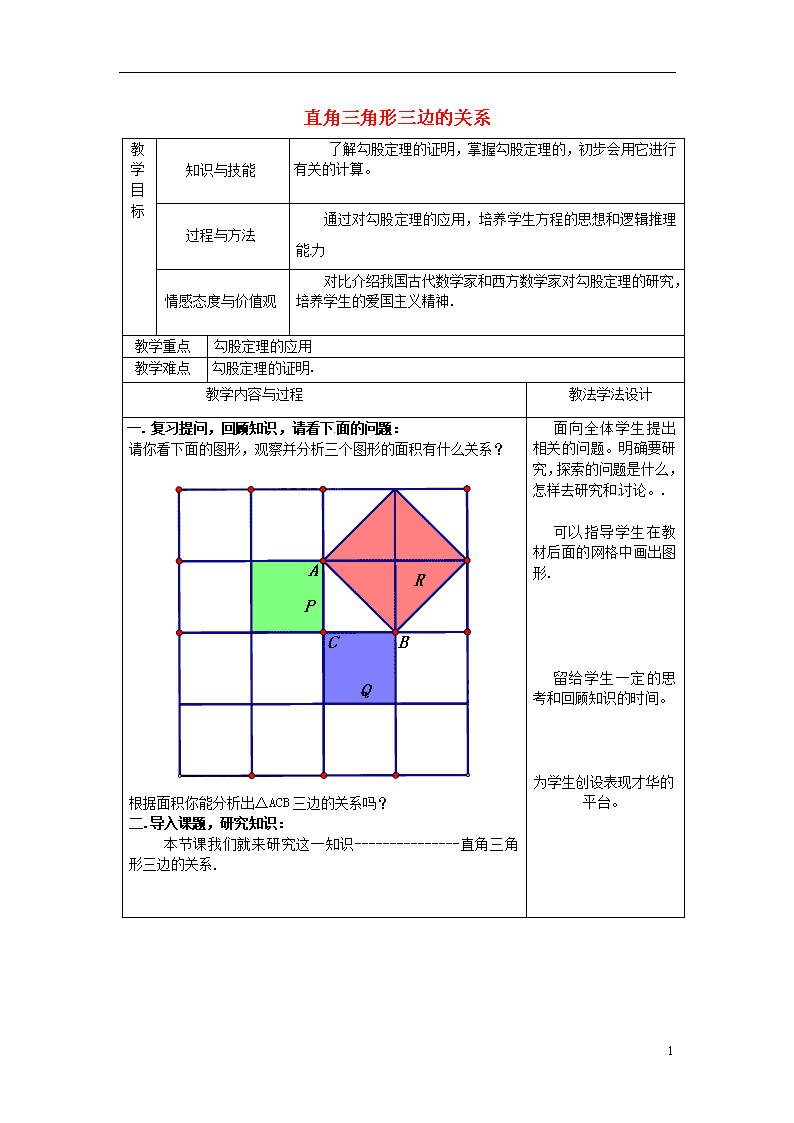
直角三角形三边的关系 教学目标 知识与技能 了解勾股定理的证明，掌握勾股定理的，初步会用它进行有关的计算。‎ 过程与方法 通过对勾股定理的应用，培养学生方程的思想和逻辑推理能力 情感态度与价值观 对比介绍我国古代数学家和西方数学家对勾股定理的研究，培养学生的爱国主义精神.‎ 教学重点 勾股定理的应用 教学难点 勾股定理的证明.‎ 教学内容与过程 教法学法设计 一. 复习提问，回顾知识，请看下面的问题：‎ 请你看下面的图形，观察并分析三个图形的面积有什么关系？‎ 根据面积你能分析出△ACB三边的关系吗？‎ 二.导入课题，研究知识：‎ 本节课我们就来研究这一知识---------------直角三角形三边的关系.‎ 面向全体学生提出相关的问题。明确要研究，探索的问题是什么，怎样去研究和讨论。.‎ 可以指导学生在教材后面的网格中画出图形.‎ 留给学生一定的思考和回顾知识的时间。‎ 为学生创设表现才华的平台。‎ 2‎ 三.归纳知识，培养能力：‎ 勾股定理：‎ 直角三角形两直角边的平方和等于斜边的平方.‎ 四.运用知识，分析解题：‎ 例2 如图，在Rt△ABC中，AC比AB长2㎝，另一直角边BC长为6㎝，‎ ‎ 求.AC的长. ‎ 五.课堂练习：‎ 练习1‎ 在RtΔABC中，∠A、∠B、∠C的对边为a、b、‎ ‎（1）已知a=6，b=8；则c= 。‎ ‎（2）已知c=25，b=15；则a= 。‎ ‎（3）已知c=19，b=13；则c= 。‎ ‎　　（结果保留根号）‎ ‎（4）已知a∶b=3：4，c=15；则b= ‎ 六.课后小结：直角三角形三边的关系.‎ 七.课后作业：复印给学生.‎ 本节课试图通过数学活动，对学生所学知识进行内化与迁移，以发展思维。同时对勾股定理的学习，对比我国数学家和西方数学家对勾股定理的研究，对学生进行爱国主义的教育，以落实素质教育的目标。‎ ‎ ‎ 教学反思 2‎