济南市2019届高三年级学习质量评估理科数学(解析版)

济南市2019届高三年级学习质量评估理科数学(解析版)

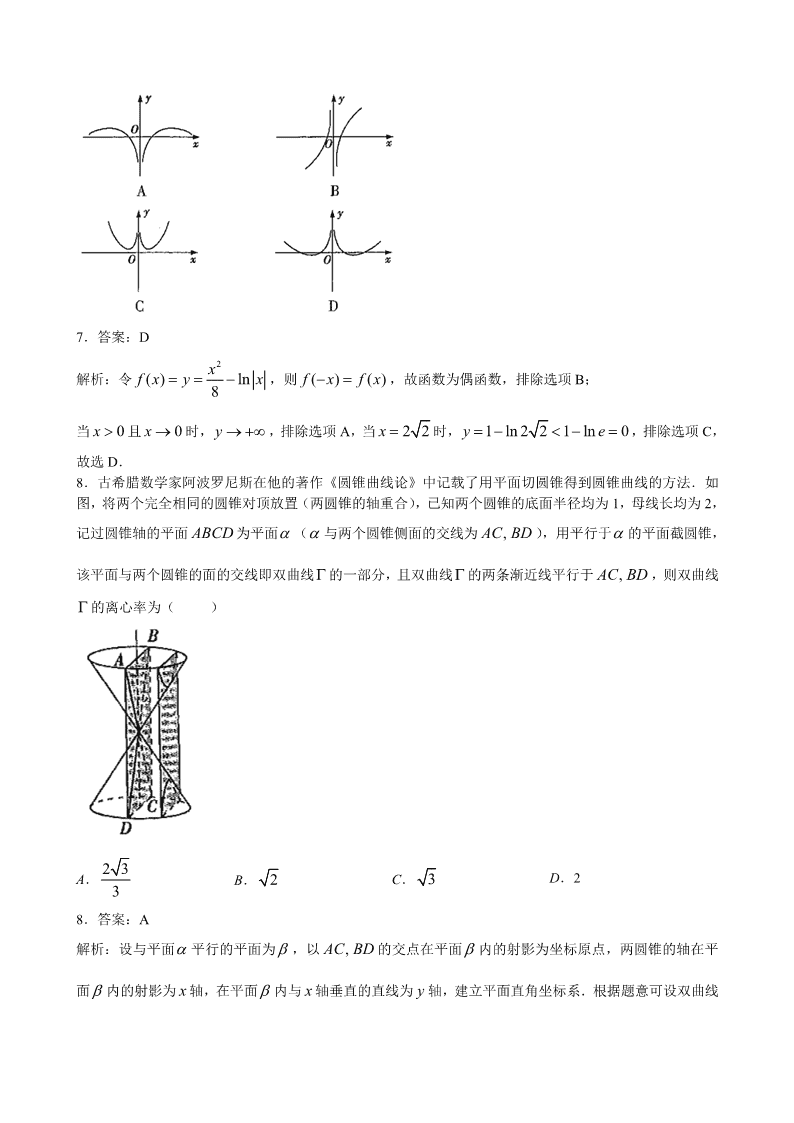
济南市 2019 届高三年级学习质量评估 理科数学 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目 要求的． 1．已知集合 2{ | 1}, { 1,0,1}A x x B  ≥ ，则 A B  （ ） A．{1} B．{ 1,1} C．{ 1,0,1} D．{ | 1}x x≥ 1．答案：B 解析： 2{ | 1} ( , 1] [1, ), { 1,0,1}A x x B      ≥ ，所以 { 1,1}A B   ． 2．已知复数 z 满足 i 2z z   （其中i 为虚数单位），则 z  （ ） A．1 i B．1 i C． 1 i  D． 1 i  2．答案：A 解析：由 i 2z z   ，得 2 2(1 i) 1 i1 i (1 i)(1 i)z       ，所以 1 iz   ． 3．已知命题 p ：关于 m 的不等式 2log 1m  的解集为{ | 2}m m  ；命题 q ：函数 3 2( ) 1f x x x   有极 值．下列命题为真命题的是（ ） A． p q B． ( )p q  C．( )p q  D．( ) ( )p q   3．答案：C 解析：由 2log 1m  ，得0 2m  ，故命题 p 为假命题； 2( ) 3 2f x x x   ，令 ( ) 0f x  得 2 3x   或 0x  ，所以 ( )f x 在 2, 3      和(0, ) 上单调递增，在 2 ,03     上单调递减，故 ( )f x 有极值，所以命 题 q 为真命题．所以( )p q  为真命题． 4．如图，在 ABC△ 中， 90 , 2, 3C BC AC     ，三角形内的空白部分是由三个半径均为 1 的扇形 构成，向 ABC△ 内随机投掷一点，则该点落在阴影部分的概率为（ ） A． 6  B．1 6  C． 4  D．1 4  4．答案：B 解析：三个空白部分的面积之和为一个半径为 1 的圆的面积的一半，即 2  ， ABC△ 的面积为 3，故所求 概率为 21 13 6     ． 5．某几何体的三视图如图所示，则该几何体的体积为（ ） A．5 B．16 3 C．6 D．8 5．答案：C 解析：该几何体是以左视图为底面的五棱柱，高为 2，底面积为 12 1 2 1 32     ，故其体积为3 2 6  ． 6．若将函数 ( ) cos 2 12f x x      的图象向左平移 8  个单位长度，得到函数 ( )g x 的图象，则下列说法正 确的是（ ） A． ( )g x 的最小正周期为 4 B． ( )g x 在区间 0, 2      上单调递减 C． ( )g x 图象的一条对称轴为 12x  D． ( )g x 图象的一个对称中心为 7 ,012      6．答案：D 解析： ( ) cos 2 cos 2 , ( )8 12 3g x x x g x                   的最小正周期为 ，选项 A 错误； 当 0, 2x     时， 42 ,3 3 3x        ，故 ( )g x 在 0, 2      上有增有减，选项 B 错误； cos 012 2g        ，故 12x  不是 ( )g x 图象的一条对称轴，选项 C 错误； 7 3cos 012 2g        ，所以 ( )g x 的图象关于点 7 ,012      对称，选项 D 正确． 7．函数 2 ln8 xy x  的图象大致为（ ） 7．答案：D 解析：令 2 ( ) ln8 xf x y x   ，则 ( ) ( )f x f x  ，故函数为偶函数，排除选项 B； 当 0x  且 0x  时，y   ，排除选项 A，当 2 2x  时， 1 ln 2 2 1 ln 0y e     ，排除选项 C， 故选 D． 8．古希腊数学家阿波罗尼斯在他的著作《圆锥曲线论》中记载了用平面切圆锥得到圆锥曲线的方法．如 图，将两个完全相同的圆锥对顶放置（两圆锥的轴重合），已知两个圆锥的底面半径均为 1，母线长均为 2， 记过圆锥轴的平面 ABCD 为平面 （ 与两个圆锥侧面的交线为 ,AC BD ），用平行于 的平面截圆锥， 该平面与两个圆锥的面的交线即双曲线 的一部分，且双曲线 的两条渐近线平行于 ,AC BD ，则双曲线  的离心率为（ ） A． 2 3 3 B． 2 C． 3 D．2 8．答案：A 解析：设与平面 平行的平面为  ，以 ,AC BD 的交点在平面  内的射影为坐标原点，两圆锥的轴在平 面  内的射影为 x 轴，在平面  内与 x 轴垂直的直线为 y 轴，建立平面直角坐标系．根据题意可设双曲线 2 2 2 2: 1( 0, 0)x y a ba b     ．由题意可得双曲线 的渐近线方程为 3 3y x  ，即 3 3 b a  ， 所以离心率 2 2 31 3 c be a a        ． 9．已知  12 0 22a b a b c a b d c               ， ， ， ，则 d  的取值范围是（ ） A．[0, 2 2] B．[0, 2] C．[0, 2] D．[0,1] 9．答案：A 解析：不妨令 (2,0), (0,2)a b   ，则 (1,1)c  ．设 ( , )d x y  ，则 2 2 2( 1) ( 1) 2d c x y        ，所 以点 ( , )x y 在以 (1,1) 为圆心、 2 为半径的圆上， d  表示点 ( , )x y 到坐标原点的距离，故 d  的取值范围 为[0, 2 2]． 10．执行如图所示的程序框图，若输入的 , ,a b c 依次为 sin cos sin(sin ) ,(sin ) , (cos )     ，其中 ,4 2       ，则输出的 x 为（ ） A． cos(cos )  B． sin(sin )  C． cos(sin )  D． sin(cos )  10．答案：C 解析：该程序框图的功能是输出 , ,a b c 中的最大者．当 ,4 2       时， 0 cos sin 1    ， 由指数函数 ( ) (cos )xf x  单调递减可得 (sin ) (cos )f f  ，即 sin cos(cos ) (cos )   ； 由幂函数 cos( )g x x  单调递增可得 (cos ) (sin )g g  ，即 cos cos(cos ) (sin )   ． 由指数函数 ( ) (sin )xh x  单调递减可得 (sin ) (cos )h h  ，即 sin cos(sin ) (sin )   ． 所以 , ,a b c 中的最大者为 cos(sin )  ，故输出的 x 为 cos(sin )  ． 11．过抛物线 2 2 ( 0)y px p  的焦点 F 作直线 l ，交抛物线于点 ,M N ，交抛物线的准线于点 P ，若 2PM PN   ，则直线l 的斜率为 （ ） A． 2 B． 2 C． 2 2 D． 4 11．答案：C 解析：如图，设点 M 在第一象限，分别过 ,M N 作抛物线准线的垂线，垂足为 ,M N  ，由 2PM PN   ， 得 N 为 MP 的中点．设 NN t  ，则 2MM t  ， 根据抛物线的定义， 3MN MF NF MM NN t      ，所以 6MP t ，在 Rt PMM △ 中， 4 2PM t  ，所以 tan 2 2PMM  ，即直线l 的斜率为 2 2 ．当点 N 在第一象限时可得直线l 的斜 率为 2 2 ．综上，直线l 的斜率为 2 2 ． 12．已知函数 2 1, 0( ) , 0x x xf x e x     ≤ ，若对任意 [ 1,1]x  ，不等式 2[(1 2 ) 4 2] [ ( )]af a x a f x   ≥ 恒 成立，其中 0a  ，则 a 的取值范围是（ ） A． 10, 3      B． 1 ,2    C． 3 ,7    D． 1 3,3 7      12．答案：B 解析： 2 0x ≥ ，当 2 0x  时， 2( ) 1f x  ，当 2 0x  时， 22( ) xf x e ，所以 22( ) xf x e ， 因为 0a  ，所以 22 2[ ( )] ( )axf x e f ax  ， 所以对任意 [ 1,1]x  ，不等式 2[(1 2 ) 4 2] [ ( )]af a x a f x   ≥ 恒成立， 即对任意 [ 1,1]x  ， 2[(1 2 ) 4 2] ( )f a x a f ax   ≥ 恒成立． 易知 ( )f x 在 ( , )  上单调递减，所以对任意 [ 1,1]x  ， 2(1 2 ) 4 2a x a ax   ≤ 恒成立， 令 2( ) (1 2 ) 4 2 (1 2 )( 2), ( )g x a x a a x h x ax        ，则函数 ( )g x 的图象是过点( 2,0) 的直线， ( )h x 的图象是顶点在坐标原点，开口向上的抛物线，若 2(1 2 ) 4 2a x a ax   ≤ 在[ 1,1] 上恒成立，则 4 2 0a  ≤ ，即 1 2a≥ ，故 a 的取值范围是 1 ,2    ． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分．把答案填在题中的横线上． 13．在 6 2 1x x     的展开式中，常数项为 ．（用数字作答） 13．答案：15 解析： 6 2 1x x     展开式中的常数项为 4 4 2 2 6 1( ) 15C x x      14．若实数 ,x y 满足约束条件 0 3 4 3 0 x x y y     ≥ ≤ ≥ ，则 4 3z x y  的最大值为 ． 14．答案：4 解析：作可行域为如图所示的 OAB△ ， 其中 3(1,0), 0, 4A B     ，则 max 94, , 44A B Az z z z     ． 15．我国《物权法》规定：建造建筑物，不得违反国家有关工程建设标准，妨碍相邻建筑物的通风、采光 和日照．已知某小区的住宅楼的底部均在同一水平面上，且楼高均为 45 m，依据规定，该小区内住宅楼楼 间距不小于 52 m．若该小区内某居民在距离楼底 27 m 高处的某阳台观测点，测得该小区内正对面住宅楼 O x y A B 楼顶的仰角和楼底的俯角之和为 45°，则该小区的住宅楼楼间距实际为 m． 15．答案：54 解析：如图，设两住宅楼楼间距实际为 mx ．根据题意可得 27 45 27 18tan , tanDCA DCBx x x      ， 又 45DCA DCB     ，所以 27 18 tan( ) 127 181 x xDCA DCB x x         ，整理得 2 45 27 18 0x x    ， 解得 54x  或 9x   （舍去）．所以该小区的住宅楼楼间距实际为54 m ． A B C D 16．已知球O 的半径为 3，该球的内接正三棱锥的体积最大值为 1V ，内接正四棱锥的体积最大值为 2V ，则 1 2 V V 的值为 ． 16．答案： 3 3 8 解析：设内接正三棱锥底面外接圆的半径为 1r ，高为 1h ，则 2 2 1 1( 3) 9h r   ，即 2 2 1 1 16r h h  ， 正三棱锥的体积  2 2 3 2 1 1 1 1 1 1 1 1 1 1 1 3 3 3( ) 3 ( 6 )3 3 4 4 4V h S h r h r h h h        ， 2 1 1 1 3( ) ( 3 12 )4V h h h    ，令 1( ) 0V h  ，得 1 4h  ，易得 1 max (4) 8 3V V V   ． 设内接正四棱锥底面外接圆的半径为 2r ，高为 2h ，则 2 2 2 2( 3) 9h r   ，即 2 2 2 2 26r h h  ， 正四棱锥的体积  2 2 3 2 0 2 2 2 2 2 2 2 1 2 2( ) 2 ( 6 )3 3 3V h r h r h h h     ， 2 0 2 2 2 2( ) ( 3 12 )3V h h h    ， 令 0 2( ) 0V h  ，得 2 4h  ，易得 2 0 64(4) 3V V  ，所以 1 2 8 3 3 3 64 8 3 V V   ． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考 生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（本小题满分 12 分） 已知数列{ }na 是递增的等差数列，满足 2 3 4 15a a a   ， 2a 是 1a 和 5a 的等比中项． （1）求数列{ }na 的通项公式； （2）设 1 1 n n n b a a   ，求数列{ }nb 的前 n 项和 nS ． 17．解析：（1）设数列{ }na 的公差为 d ，由 2 3 4 15a a a   ，得 3 5a  ， 由 2a 是 1a 和 5a 的等比中项，得 2 2 1 5a a a  ，所以 2(5 ) (5 2 )(5 2 )d d d    ，解得 0d  或 2d  ． 因为数列{ }na 为递增数列，所以 2d  ．所以 2 1na n  ．…………………………………………6 分 （2） 1 1 1 1 (2 1) (2 1) 1 1 1 (2 1)(2 1) 2 (2 1)(2 1) 2 2 1 2 1n n n n nb a a n n n n n n                  ， 所以 1 1 1 1 1 1 1 11 12 3 3 5 2 1 2 1 2 2 1 2 1n nS n n n n                                       ．………………12 分 18．（本小题满分 12 分） 如图，在四棱锥 P ABCD 中，底面 ABCD 为正方形，PA  平面 ABCD ，E 为 AD 的中点，AC 交 BE 于点 F ，G 为 PCD△ 的重心． （1）求证： //FG 平面 PAD ； （2）若 PA PD ，点 H 在线段 PD 上，且 2PH HD ，求二面角 H FG C  的余弦值． P A B C D F E G H 18．解析：（1）因为 //AE BC ，所以 AEF CBF△ ∽△ ，因为 E 为 AD 的中点，所以 2AE AD BC  ， 所以 2CF AF ． 如图，延长 CG ，交 PD 于 M ，连接 AM ，因为 G 为 PCD△ 的重心，所以 M 为 PD 的中点，且 2CG GM ，所以 //FG AM ， 因为 AM  平面 PAD ，FG  平面 PAD ，所以 //FG 平面 PAD ．……………………………………6 分 （2）以 A 为坐标原点，分别以 , ,AB AD AP 所在的直线分别为 x 轴， y 轴， z 轴建立如图所示空间直角 坐标系．设 3PA AD  ，则 (3,3,0), (0,3,0), (0,0,3), (1,1,0)C D P F ．因为 2PH HD ，所以 (0, 2,1)H ． 因为G 为 PCD△ 的重心，所以 (1,2,1)G ． (2, 2,0), (0,1,1), ( 1,1,1)FC FG FH       ， 设平面 FGC 的法向量为 1 1 1 1( , , )n x y z  ， 则 1 1 1 1 1 1 2 2 0 0 n FC x y n FG y z              ，取 1 1x  ，则 1 11, 1y z   ，所以 1 (1, 1,1)n    ． 设平面 FGH 的法向量为 2 2 2 2( , , )n x y z  ， 则 2 2 2 2 2 2 0 0 n FH x y z n FG y z                ，取 2 1y  ，则 2 20, 1x z   ，所以 2 (0,1, 1)n    ． 所以 1 2 1 2 1 2 6cos , 3 n nn n n n          ．由图可知，该二面角为钝角， 所以二面角 H FG C  的余弦值为 6 3 ．…………………………………………………………12 分 P A B C D F E G H x y z P A B C D F E G H M 19．（本小题满分 12 分） 已知椭圆 2 2 2 2: 1( 0)x yC a ba b    的离心率为 3 2 ，右焦点为 F ，且该椭圆过点 31, 2      ． （1）求椭圆C 的方程； （2）当动直线l 与椭圆C 相切于点 A ，且与直线 4 3 3x  相交于点 B 时，求证： FAB△ 为直角三角形． 19．解析：（1）由题意得 2 2 3 1 3, 12 4 c a a b   ，又 2 2 2a b c  ，所以 2 21, 4b a  ，即椭圆C 的方程 为 2 2 14 x y  ．………………………………………………………………………………………………4 分 （2）由题意可得直线l 的斜率存在，设 :l y kx m  ，联立得 2 2 14 y kx m x y     ， 得 2 2 2(4 1) 8 4 4 0k x kmx m     ， 判别式 2 2 2 264 16(4 1)( 1) 0k m k m      ，得 2 24 1m k  ．………………………………6 分 设 1 1( , )A x y ，则 2 1 1 12 2 8 8 4 4 1,2(4 1) 2 km km k kx y kx m mk m m m m            ，即 4 1,kA m m     ． 易得 4 3 4 3, , ( 3,0)3 3B k m F     ，则 4 1 3 4 33, , ,3 3 kFA FB k mm m                 ， 3 4 1 4 3 4 3 4 33 1 1 03 3 3 3 k k kFA FB k mm m m m                        ，…………………………11 分 所以 FA FB   ，即 FAB△ 为直角三角形，得证．…………………………………………………………12 分 A FO B 20．（本小题满分 12 分） 某医药公司研发生产一种新的保健产品，从一批产品中随机抽取 200 盒作为样本，测量产品的一项质量指 标值，该指标值越高越好．由测量结果得到如下频率分布直方图： （1）求 a，并试估计这 200 盒产品的该项指标值的平均值． （2）①由样本估计总体，结合频率分布直方图认为该产品的该项质量指标值 服从正态分布 2( ,10 )N  ， 计算该产品该项指标值落在 (180,220]上的概率； ②国家有关部门固定每盒产品该项指标值不低于 150 均为合格，且按该项指标值从低到高依次分为：合格、 优良、优秀三个等级，其中 (180,220]为优良，不高于 180 为合格，高于 220 为优秀，在①的条件下，设 该公司生产该产品 1 万盒的成本为 15 万元，市场上各等级每盒该产品的售价（单位：元）如表，求该公 司每万盒的平均利润． 等级 合格 优良 优秀 售价 10 20 30 附：若 2( , )N  ～ ，则 ( ) 0.6827, ( 2 2 ) 0.9545P P                   ． 20．解析：（1）由10 (2 0.002 0.008 0.009 0.022 0.024 ) 1a        ，解得 0.033a  ，………2 分 则平均值 0.02 170 0.09 180 0.22 190 0.33 200 0.24 210 0.08 200 0.02 230 200x                ， 即这 200 盒产品的该项指标值的平均值为 200．……………………………………………………………5 分 （2）①由题意可得 200, 10 x   ， 则 ( 2 2 ) (180 220) 0.9545P P          ≤ ≤ ．…………………………………………8 分 ②设每盒该产品的售价为 X 元，由①可得 X 的分布列为 X 10 20 30 P 0.02275 0.9545 0.02275 则每盒该产品的平均售价为 ( ) 10 0.02275 20 0.9545 30 0.02275 20E X        元， 故每万盒的平均利润为 20 15 5  （万元）．…………………………………………………………12 分 21．（本小题满分 12 分）已知函数 21( ) ( 1)2 x xf x e a e ax    ． （1）讨论 ( )f x 的单调性； （2）若 ( )f x 有两个零点，求 a 的取值范围． 21．（1） 2( ) ( 1) ( 1)( )x x x xf x e a e a e e a        ， （i）若 0a ≤ ， 当 ( ,0)x  时， ( ) 0, ( )f x f x  单调递减；当 (0, )x  时， ( ) 0, ( )f x f x  单调递增． （ii）当 0a  时，令 ( ) 0f x  ，则 1 20, lnx x a  ， 若 1a  ，则 1 2 , ( ) 0x x f x ≥ 恒成立， ( )f x 在( , )  上单调递增． 若 0 1a  ，则 1 2x x ，当 ( ,ln )x a  时， ( ) 0, ( )f x f x  单调递增； 当 (ln ,0)x a 时， ( ) 0, ( )f x f x  单调递减；当 (0, )x  时， ( ) 0, ( )f x f x  单调递增． 若 1a  ，则 1 2x x ，当 ( ,0)x  时， ( ) 0, ( )f x f x  单调递增； 当 (0,ln )x a 时， ( ) 0, ( )f x f x  单调递减；当 (ln , )x a  时， ( ) 0, ( )f x f x  单调递增． 综上所述，当 a ≤0 时， ( )f x 在 ( ,0) 上单调递减，在(0, ) 上单调递增； 当 1a  时， ( )f x 在( , )  上单调递增； 当 0 1a  时， ( )f x 在( ,ln )a 上单调递增，在(ln ,0)a 上单调递减，在(0, ) 上单调递增； 当 1a  时， ( )f x 在( ,0) 上单调递增，在(0,ln )a 上单调递减，在(ln , )a  上单调递增．……5 分 （2）（i）当 0a  时， 21 1( ) 12 2 x x x xf x e e e e       ，令 ( ) 0f x  ，得 ln 2x  ，此时只有一个零点， 不合题意． （ii）当 0a  时，由（1）可知， ( )f x 在 ( ,0) 上单调递减，在(0, ) 上单调递增，若 ( )f x 有两个零 点，则 1(0) 02f a    ，即 1 2a   ．注意到 2 21 1 1(1) ( 1) (1 ) ( 1) 02 2 2f e a a e e e a e e a e               ， 所以当 (0,1)x 时， ( )f x 有一个零点． 当 0x  时， 1( ) 1 ( ) ( 1)2 x x xf x ax e e a ax a x e ax a             ， 取 0 11 0x a   ，则 0( ) 0f x  ，所以当 0( ,0)x x 时， ( )f x 有一个零点． 所以当 1 02 a   时， ( )f x 有两个零点，符合题意． （iii）当 1a  时， ( )f x 在 ( , )  上单调递增，不可能有两个零点，不合题意． （iv）当 0 1a  时， ( )f x 在( ,ln )a 上单调递增，在(ln ,0)a 上单调递减，在(0, ) 上单调递增． 2ln ln 2 21 1 1(ln ) ( 1) ln ln ln 12 2 2 a af a e a e a a a a a a a a a a              ， 因为 1ln 1 02a a   ，所以 (ln ) 0f a  ，此时 ( )f x 最多有一个零点，不合题意． （v）当 1a  时， ( )f x 在 ( ,0) 上单调递增，在(0,ln )a 上单调递减，在(ln , )a  上单调递增． 因为 1(0) 02f a    ，所以此时 ( )f x 最多有一个零点，不合题意． 综上所述，若 ( )f x 有两个零点，则 a 的取值范围是 1 ,02     ．………………………………12 分 （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所作的第一题计分． 22．【选修 4—4：坐标系与参数方程】（本小题满分 10 分） 在平面直角坐标系 xOy 中，以坐标原点O 为极点， x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标 方程为 2cos sin   ，直线l 的参数方程为 3 2 1 2 x t y a t      （t 为参数），其中 0a  ，直线l 与曲线C 相交 于 ,M N 两点． （1）求曲线C 的直角坐标方程； （2）若点 (0, )P a 满足 1 1 4PM PN  ，求 a 的值． 22．解析：（1）由 2cos sin   ，得 2 2cos sin    ，由 cos , sinx y     ，得曲线C 的直 角坐标方程为 2y x ．…………………………………………………………………………………4 分 （2）将直线l 的参数方程 3 2 1 2 x t y a t      （t 为参数）代入 2y x ，得 23 1 10, 3 04 2 4t t a a       ． 设 ,M N 对应的参数分别为 1 2,t t ，则 1 2 1 2 2 4,3 3 at t t t    ， 所以 2 1 2 1 2 1 2 1 2 1 2 4 44( ) 4 9 31 1 44 3 a PM PN t t t t t t aPM PN PM PN t t t t                 ． 化简得： 264 12 1 0a a   ，解得 1 4a  或 1 16a   （舍去），所以 1 4a  ．……………………10 分 23．【选修 4—5：不等式选讲】（本小题满分 10 分） 已知函数 ( ) 3 3f x x x a    ． （1）当 2a  时，求不等式 ( ) 4f x  的解集； （2）若 ( ) 3 4f x x  对任意的 ( 1, )x   恒成立，求 a 的取值范围． 23．解析：（1）当 2a  时， ( ) 3 3 2f x x x    ，即 4 1, 1 ( ) 2 5, 1 2 4 1, 2 x x f x x x x x           ≤ ≥ ， 当 1x ≤ 时，不等式 ( ) 4f x  即 4 1 4x   ，解得 5 4x   ，所以 5 4x   ； 当 1 2x   时，不等式 ( ) 4f x  即 2 5 4x   ，解得 1 2x   ，所以 1 22 x   ； 当 2x≥ 时，不等式 ( ) 4f x  即 4 1 4x   ，解得 3 4x  ，所以 2x≥ ． 所以不等式 ( ) 4f x  的解集为 5 1, ,4 2               ．………………………………………………5 分 （2）由题意知，当 1x   时， ( ) 3 3 3 4f x x x a x      恒成立，即 1x a  在 ( 1, )x   上恒 成立．作出函数 y x a  的图象，由图易知， 1 1 1 a a     ≥ ，解得 2a ≤ ． 所以 a 的取值范围为( , 2]  ．…………………………………………………………………………10 分 1 -1 Oa