【数学】2021届一轮复习人教A版(文)第一章 第2讲 命题及其关系、充分条件与必要条件学案
第2讲 命题及其关系、充分条件与必要条件
一、知识梳理
1.命题
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
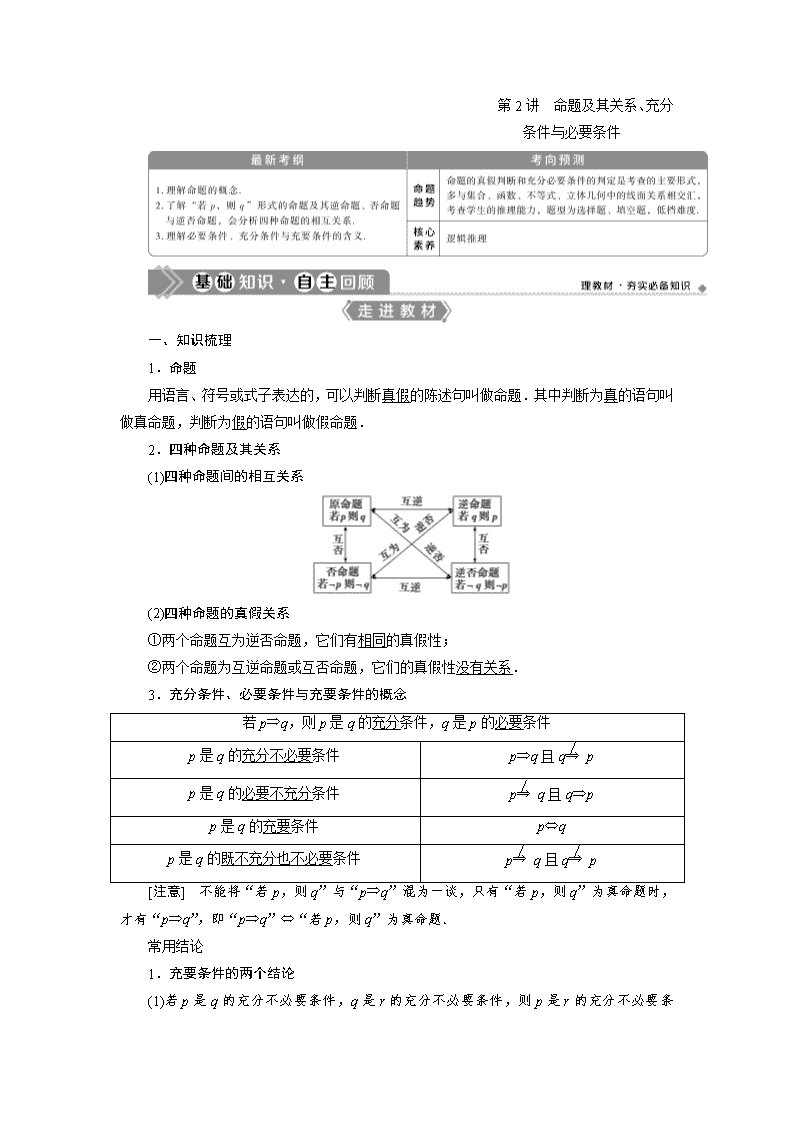
2.四种命题及其关系
(1)四种命题间的相互关系
(2)四种命题的真假关系
①两个命题互为逆否命题,它们有相同的真假性;
②两个命题为互逆命题或互否命题,它们的真假性没有关系.
3.充分条件、必要条件与充要条件的概念
若p⇒q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
p⇒q且q p
p是q的必要不充分条件
p q且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分也不必要条件
p q且q p
[注意] 不能将“若p,则q”与“p⇒q”混为一谈,只有“若p,则q”为真命题时,才有“p⇒q”,即“p⇒q”⇔“若p,则q”为真命题.
常用结论
1.充要条件的两个结论
(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r
的充分不必要条件.
(2)若p是q的充分不必要条件,则綈q是綈p的充分不必要条件.
2.一些常见词语及其否定
词语
是
都是
都不是
等于
大于
否定
不是
不都是
至少一个是
不等于
不大于
二、习题改编
1.(选修11P8A组T2改编)命题“若x2>y2,则x>y”的逆否命题是( )
A.“若x
y,则x2>y2”
C.“若x≤y,则x2≤y2” D.“若x≥y,则x2≥y2”
解析:选C.根据原命题和逆否命题的条件和结论的关系得命题“若x2>y2,则x>y”的逆否命题是“若x≤y,则x2≤y2”.故选C.
2.(选修11P10练习T3(2)改编)“(x-1)(x+2)=0”是“x=1”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选B.若x=1,则(x-1)(x+2)=0显然成立,但反之不成立,即若(x-1)(x+2)=0,则x的值也可能为-2.故选B.
一、思考辨析
判断正误(正确的打“√”,错误的打“×”)
(1)“x2+2x-3<0”是命题.( )
(2)命题“若p,则q”的否命题是“若p,则綈q”.( )
(3)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至少有一个为真.( )
(4)当q是p的必要条件时,p是q的充分条件.( )
(5)q不是p的必要条件时,“p q”成立.( )
答案:(1)× (2)× (3)√ (4)√ (5)√
二、易错纠偏
(1)不明确命题的条件与结论;
(2)对充分必要条件判断错误;
(3)含有大前提的命题的否命题易出错.
1.命题“若△ABC有一内角为,则△ABC的三个内角成等差数列”的逆命题( )
A.与原命题同为假命题
B.与原命题的否命题同为假命题
C.与原命题的逆否命题同为假命题
D.与原命题同为真命题
解析:选D.原命题显然为真,原命题的逆命题为“若△ABC的三个内角成等差数列,则△ABC有一内角为”,它是真命题.
2.已知p:a<0,q:a2>a,则綈p是綈q的________条件(填:充分不必要、必要不充分、充要、既不充分也不必要).
解析:綈p:a≥0;綈q:a2≤a,即0≤a≤1,故綈p是綈q的必要不充分条件.
答案:必要不充分
3.已知命题“对任意a,b∈R,若ab>0,则a>0”,则它的否命题是____________.
答案:存在a,b∈R,若ab≤0,则a≤0.
四种命题的相互关系及其真假判断(师生共研)
(2020·长春质量检测(二))命题“若x2<1,则-11或x<-1,则x2>1
D.若x≥1或x≤-1,则x2≥1
【解析】 命题的形式是“若p,则q”,由逆否命题的知识,可知其逆否命题为“若綈q,则綈p”的形式,所以“若x2<1,则-10);q:x<或x>1,若p是q的充分不必要条件,则实数m的取值范围为______.
解析:因为p是q的充分不必要条件,又m>0,所以≤,所以00).若綈p是綈q的充分不必要条件,则m的取值范围为______.
【解析】 条件p:-2≤x≤10,条件q:1-m≤x≤1+m,又綈p是綈q的充分不必要条件,则q是p的充分不必要条件.故有,所以0b2”是“a>b”的充分条件
B.“a2>b2”是“a>b”的必要条件
C.“ac2>bc2”是“a>b”的充分条件
D.“|a|>|b|”是“a>b”的充要条件
解析:选C.对于A,当a=-5,b=1时,满足a2>b2,但是ab,但是a2bc2得c≠0,则有a>b成立,即充分性成立,故正确;对于D,当a=-5,b=1时,|a|>|b|成立,但是ab,但是|a|<|b|,
所以必要性也不成立,故“|a|>|b|”是“a>b”的既不充分也不必要条件.故选C.
4.已知命题α:如果x<3,那么x<5;命题β:如果x≥3,那么x≥5;命题γ:如果x≥5,那么x≥3.关于这三个命题之间的关系中,下列说法正确的是( )
①命题α是命题β的否命题,且命题γ是命题β的逆命题;②命题α是命题β的逆命题,且命题γ是命题β的否命题;③命题β是命题α的否命题,且命题γ是命题α的逆否命题.
A.①③ B.②
C.②③ D.①②③
解析:选A.本题考查命题的四种形式,逆命题是把原命题中的条件和结论互换,否命题是把原命题中的条件和结论都加以否定,逆否命题是把原命题中的条件与结论先都否定然后互换所得,故①正确,②错误,③正确.
5.“(x+1)(y-2)=0”是“x=-1且y=2”的________条件.
解析:因为(x+1)(y-2)=0,所以x=-1或y=2,所以(x+1)(y-2)=0 x=-1且y=2,x=-1且y=2⇒(x+1)(y-2)=0,所以是必要不充分条件.
答案:必要不充分
6.已知命题p:x≤1,命题q:<1,则綈p是q的______.
解析:由题意,得綈p:x>1,q:x<0或x>1,故綈p是q的充分不必要条件.
答案:充分不必要条件
7.若命题“ax2-2ax-3>0不成立”是真命题,则实数a的取值范围是________.
解析:由题意知ax2-2ax-3≤0恒成立,
当a=0时,-3≤0成立;当a≠0时,得
解得-3≤a<0,故-3≤a≤0.
答案:[-3,0]
8.已知命题p:(x+3)(x-1)>0;命题q:x>a2-2a-2.若綈p是綈q的充分不必要条件,求实数a的取值范围.
解:已知p:(x+3)(x-1)>0,可知p:x>1或x<-3,因为綈p是綈q的充分不必要条件,所以q是p的充分不必要条件,得a2-2a-2≥1,解得a≤-1或a≥3,即a∈(-∞,-1]∪[3,+∞).
[综合题组练]
1.(创新型)(2020·抚州七校联考)A,B,C三个学生参加了一次考试,A,B的得分均为70分,C的得分为65分.已知命题p:若及格分低于70分,则A,B,C都没有及格.则下列四个命题中为p的逆否命题的是( )
A.若及格分不低于70分,则A,B,C都及格
B.若A,B,C都及格,则及格分不低于70分
C.若A,B,C至少有一人及格,则及格分不低于70分
D.若A,B,C至少有一人及格,则及格分高于70分
解析:选C.根据原命题与它的逆否命题之间的关系知,命题p的逆否命题是若A,B,C至少有一人及格,则及格分不低于70分.故选C.
2.(2020·辽宁丹东质量测试(一))已知x,y∈R,则“x+y≤1”是“x≤且y≤”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
解析:选B.当“x+y≤1”时,如x=-4,y=1,满足x+y≤1,但不满足“x≤且y≤”.当“x≤且y≤”时,根据不等式的性质有“x+y≤1”.故“x+y≤1”是“x≤且y≤”的必要不充分条件.故选B.
3.(2020·湖南雅礼中学3月月考)若关于x的不等式|x-1|3 D.a≥3
解析:选D.|x-1|0”的否命题为“若x≥-1,则x2-2x-3≤0”.
解析:当x<0时,x+≤-2,故①是假命题;根据逆否命题的定义可知,②是真命题;“a=±1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件,故③是假命题;根据否命题的定义知④是真命题.
答案:②④