2020届九年级数学下册 第6章 二次函数 6

2020届九年级数学下册 第6章 二次函数 6

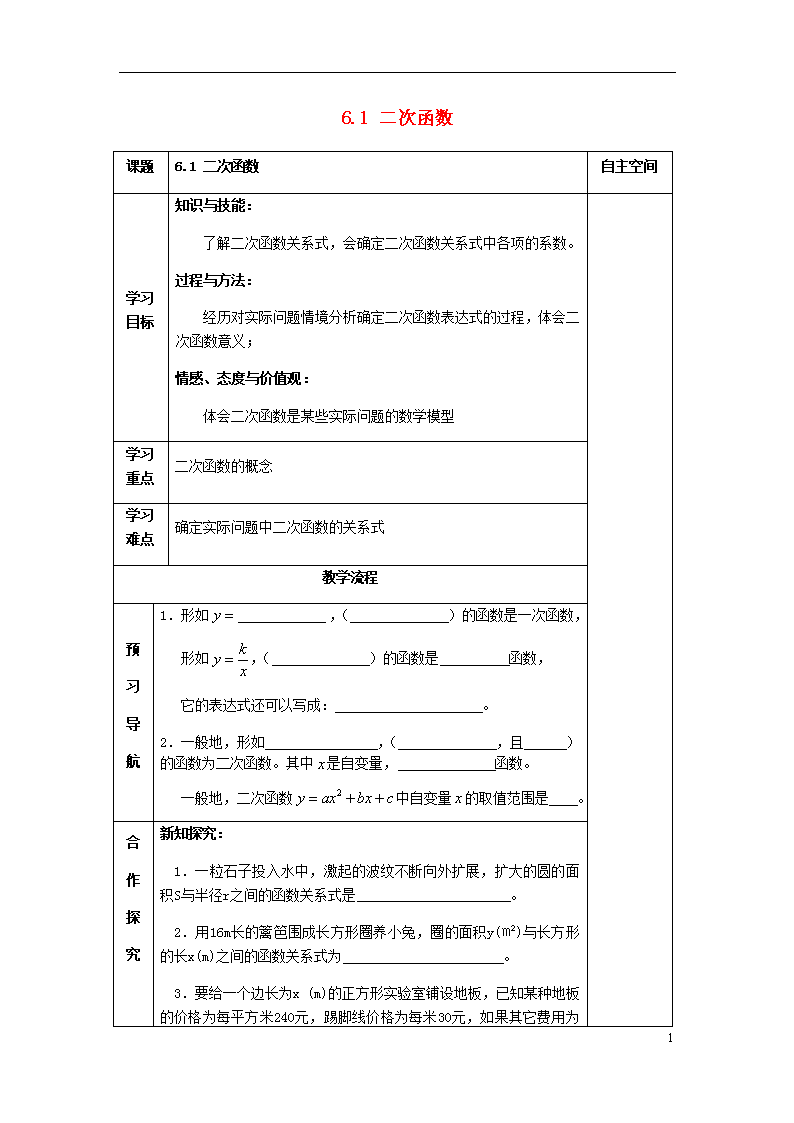
‎6.1 二次函数 课题 ‎6.1 二次函数 自主空间 学习目标 知识与技能：‎ 了解二次函数关系式，会确定二次函数关系式中各项的系数。‎ 过程与方法：‎ 经历对实际问题情境分析确定二次函数表达式的过程，体会二次函数意义；‎ 情感、态度与价值观：‎ 体会二次函数是某些实际问题的数学模型 学习重点 二次函数的概念 学习难点 确定实际问题中二次函数的关系式 教学流程 预 习 导 航 ‎1．形如，（ ）的函数是一次函数，‎ 形如，（ ）的函数是 函数，‎ 它的表达式还可以写成： 。‎ ‎2．一般地，形如 ，（ ，且 ）的函数为二次函数。其中是自变量， 函数。‎ 一般地，二次函数中自变量的取值范围是 。‎ 合 作 探 究 新知探究：‎ ‎1．一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S与半径r之间的函数关系式是 。‎ ‎2．用‎16m长的篱笆围成长方形圈养小兔，圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为 。‎ ‎3．要给一个边长为x (m)的正方形实验室铺设地板，已知某种地板的价格为每平方米240元，踢脚线价格为每米30元，如果其它费用为 4‎ ‎1000元，那么总费用y（元）与x（m）之间的函数关系式是 。‎ 上述函数函数关系有哪些共同之处？它们与一次函数、反比例函数的关系式有什么不同？‎ 例题分析： ‎ 例1．当k为何值时，函数为二次函数？‎ 例2．写出下列各函数关系，并判断它们是什么类型的函数．‎ ‎⑴圆的面积y（cm2）与它的周长x（cm）之间的函数关系；‎ ‎⑵某种储蓄的年利率是1.98%，存入10000元本金，若不计利息，求本息和y（元）与所存年数x之间的函数关系；‎ ‎⑶菱形的两条对角线的和为‎26cm，求菱形的面积S（cm2）与一对角线长x（cm）之间的函数关系．‎ 例3.已知二次函数，当时，。当时，求的值．‎ 展示交流：‎ ‎1.考察下列函数：①，②，③，④，⑤（是自变量）中，二次函数是： 。‎ ‎2.若一个边长为cm的无盖正方体形纸盒的表面积为cm，则 4‎ ‎，其中的取值范围是 。‎ ‎3. 如图在长‎200米，宽‎80米的矩形广场内修建等宽的十字形道路，请写出绿地面积(㎡)与路宽(m)之间的函数关系式： 。‎ ‎4. 如图，用‎50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积(㎡)与它与墙平行的边的长(m)之间的函数关系式： 。‎ ‎5.已知函数是二次函数，求m的值．‎ 四、提炼总结：‎ 当 堂 达 标 ‎1．已知二次函数y=ax2+bx+c（其中a、b、c为常数），当a_____时，是二次函数；当a_______，b_______时，是一次函数；当a______，b_____，c______时，是正比例函数．‎ ‎2．化工厂在一月份生产某种产品200t，三月份生产yt，则y与月平均增长率x的关系是__________________．‎ ‎3．把函数y=（2－3x）（6－x）化成y=ax2+bx+c（a≠0）的形式__________________．‎ 4‎ ‎4．根据如图1所示的程序计算函数值:‎ ‎ （1）当输入的x的值为时，输出的结果为________．‎ ‎（2）当输入的数为______时，输出的值为－4．‎ ‎ ‎ ‎5．下列函数关系式中，二次函数的个数有（ ）‎ ‎ （1）y=x2+2xz+5； （2）y=－5+8x－x2；‎ ‎（3）y=（3x+2）（4x－3）－12x2； （4）y=ax2+bx+c； ‎ ‎（5）y=mx2+x；（6）y=bx2+1（b≠0）;（7）y=x2+kx+20（k为常数）‎ ‎ A．1 B．‎2 C．3 D．4‎ ‎6．若y=（m－3）是二次函数，求m的值．‎ 学习反思：‎ 4‎