高考理科数学专题复习练习14.1几何证明选讲

高考理科数学专题复习练习14.1几何证明选讲

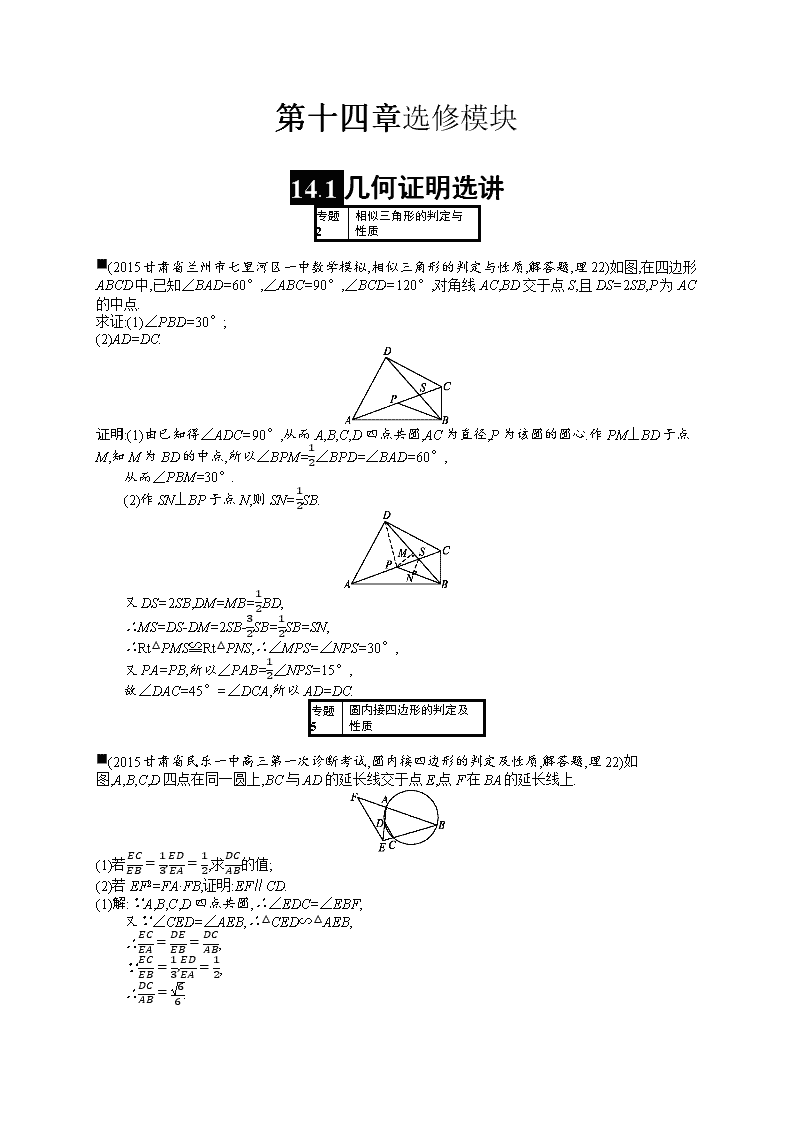
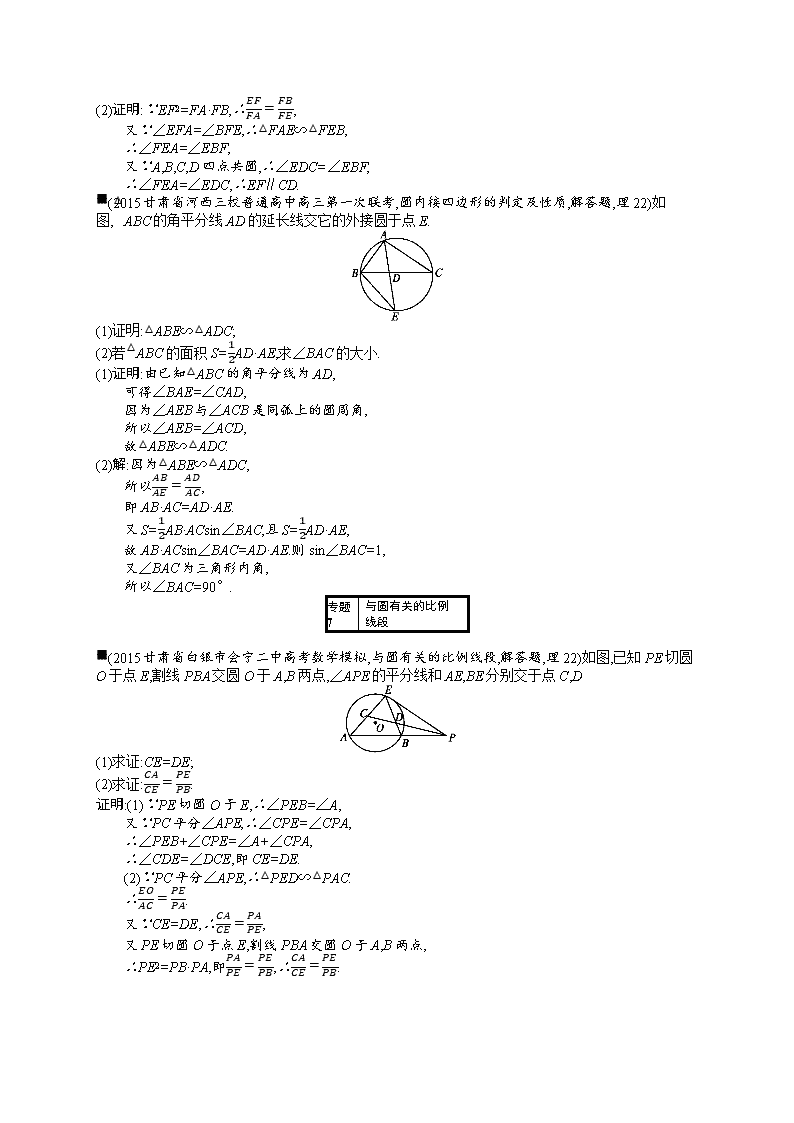
第十四章选修模块 ‎14.1几何证明选讲 专题2‎ 相似三角形的判定与性质 ‎■(2015甘肃省兰州市七里河区一中数学模拟,相似三角形的判定与性质,解答题,理22)如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.‎ 求证:(1)∠PBD=30°;‎ ‎(2)AD=DC.‎ 证明:(1)由已知得∠ADC=90°,从而A,B,C,D四点共圆,AC为直径,P为该圆的圆心.作PM⊥BD于点M,知M为BD的中点,所以∠BPM=‎1‎‎2‎∠BPD=∠BAD=60°,‎ 从而∠PBM=30°.‎ ‎(2)作SN⊥BP于点N,则SN=‎1‎‎2‎SB.‎ 又DS=2SB,DM=MB=‎1‎‎2‎BD,‎ ‎∴MS=DS-DM=2SB-‎3‎‎2‎SB=‎1‎‎2‎SB=SN,‎ ‎∴Rt△PMS≌Rt△PNS,∴∠MPS=∠NPS=30°,‎ 又PA=PB,所以∠PAB=‎1‎‎2‎∠NPS=15°,‎ 故∠DAC=45°=∠DCA,所以AD=DC.‎ 专题5‎ 圆内接四边形的判定及性质 ‎■(2015甘肃省民乐一中高三第一次诊断考试,圆内接四边形的判定及性质,解答题,理22)如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.‎ ‎(1)若ECEB‎=‎1‎‎3‎,EDEA=‎‎1‎‎2‎,求DCAB的值;‎ ‎(2)若EF2=FA·FB,证明:EF∥CD.‎ ‎(1)解:∵A,B,C,D四点共圆,∴∠EDC=∠EBF,‎ 又∵∠CED=∠AEB,∴△CED∽△AEB,‎ ‎∴ECEA‎=DEEB=‎DCAB,‎ ‎∵ECEB‎=‎1‎‎3‎,EDEA=‎‎1‎‎2‎,‎ ‎∴DCAB‎=‎‎6‎‎6‎.‎ ‎(2)证明:∵EF2=FA·FB,∴EFFA‎=‎FBFE,‎ 又∵∠EFA=∠BFE,∴△FAE∽△FEB,‎ ‎∴∠FEA=∠EBF,‎ 又∵A,B,C,D四点共圆,∴∠EDC=∠EBF,‎ ‎∴∠FEA=∠EDC,∴EF∥CD.‎ ‎■(2015甘肃省河西三校普通高中高三第一次联考,圆内接四边形的判定及性质,解答题,理22)如图,△ABC的角平分线AD的延长线交它的外接圆于点E.‎ ‎(1)证明:△ABE∽△ADC;‎ ‎(2)若△ABC的面积S=‎1‎‎2‎AD·AE,求∠BAC的大小.‎ ‎(1)证明:由已知△ABC的角平分线为AD,‎ 可得∠BAE=∠CAD,‎ 因为∠AEB与∠ACB是同弧上的圆周角,‎ 所以∠AEB=∠ACD,‎ 故△ABE∽△ADC.‎ ‎(2)解:因为△ABE∽△ADC,‎ 所以ABAE‎=‎ADAC,‎ 即AB·AC=AD·AE.‎ 又S=‎1‎‎2‎AB·ACsin∠BAC,且S=‎1‎‎2‎AD·AE,‎ 故AB·ACsin∠BAC=AD·AE.则sin∠BAC=1,‎ 又∠BAC为三角形内角,‎ 所以∠BAC=90°.‎ 专题7‎ 与圆有关的比例线段 ‎■(2015甘肃省白银市会宁二中高考数学模拟,与圆有关的比例线段,解答题,理22)如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D ‎(1)求证:CE=DE;‎ ‎(2)求证:CACE‎=‎PEPB.‎ 证明:(1)∵PE切圆O于E,∴∠PEB=∠A,‎ 又∵PC平分∠APE,∴∠CPE=∠CPA,‎ ‎∴∠PEB+∠CPE=∠A+∠CPA,‎ ‎∴∠CDE=∠DCE,即CE=DE.‎ ‎(2)∵PC平分∠APE,∴△PED∽△PAC.‎ ‎∴EOAC‎=‎PEPA.‎ 又∵CE=DE,∴CACE‎=‎PAPE,‎ 又PE切圆O于点E,割线PBA交圆O于A,B两点,‎ ‎∴PE2=PB·PA,即PAPE‎=‎PEPB,∴CACE‎=‎PEPB.‎ ‎14.2坐标系与参数方程 专题6‎ 极坐标方程与参数方程的应用 ‎■(2015甘肃省民乐一中高三第一次诊断考试,极坐标方程与参数方程的应用,解答题,理23)已知曲线C1的参数方程为x=-2+‎10‎cosθ,‎y=‎10‎sinθ(θ为参数),曲线C2的极坐标方程为ρ=2cos θ+6sin θ.‎ ‎(1)将曲线C1的参数方程化为普通方程,将曲线C2的极坐标方程化为直角坐标方程;‎ ‎(2)曲线C1,C2是否相交,若相交请求出公共弦的长,若不相交,请说明理由.‎ 解:(1)由x=-2+‎10‎cosθ,‎y=‎10‎sinθ得(x+2)2+y2=10.‎ ‎∴曲线C1的普通方程为(x+2)2+y2=10.‎ ‎∵ρ=2cos θ+6sin θ,∴ρ2=2ρcos θ+6ρsin θ.‎ ‎∵ρ2=x2+y2,x=ρcos θ,y=ρsin θ,‎ ‎∴x2+y2=2x+6y,即(x-1)2+(y-3)2=10.‎ ‎∴曲线C2的直角坐标方程为(x-1)2+(y-3)2=10.‎ ‎(2)∵圆C1的圆心为(-2,0),圆C2的圆心为(1,3),‎ ‎∴|C1C2|=‎(-2-1‎)‎‎2‎+(0-3‎‎)‎‎2‎=3‎2‎<2‎10‎.‎ ‎∴两圆相交,‎ 设相交弦长为d,因为两圆半径相等,所以公共弦平分线段C1C2.‎ ‎∴d‎2‎‎2‎‎+‎‎3‎‎2‎‎2‎‎2‎=(‎10‎)2.∴d=‎22‎.‎ ‎■(2015甘肃省白银市会宁二中高考数学模拟,极坐标方程与参数方程的应用,解答题,理23)选修4—4:坐标系与参数方程 在平面直角坐标系xOy中,曲线C1的参数方程为x=4cosθ,‎y=3sinθ(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,得曲线C2的极坐标方程为ρ+6sin θ-8cos θ=0(ρ≥0).‎ ‎(1)化曲线C1的参数方程为普通方程,化曲线C2的极坐标方程为直角坐标方程;‎ ‎(2)直线l:x=2+t,‎y=-‎3‎‎2‎+λt(t为参数)过曲线C1与y轴负半轴的交点,求与直线l平行且与曲线C2相切的直线方程.‎ 解:(1)由曲线C1的参数方程为x=4cosθ,‎y=3sinθ(θ为参数),消去参数θ化为普通方程x‎2‎‎16‎‎+‎y‎2‎‎9‎=1;‎ 由曲线C2的极坐标方程为ρ+6sin θ-8cos θ=0(ρ≥0)得ρ2+6ρsin θ-8ρcos θ=0化为直角坐标方程x2+y2+6y-8x=0可化为(x-4)2+(y+3)2=25.‎ ‎(2)由曲线C1的方程x‎2‎‎16‎‎+‎y‎2‎‎9‎=1,令x=0得y=±3,‎ ‎∴曲线C1与y轴负半轴的交点为(0,-3);‎ ‎∵直线l:x=2+t,‎y=-‎3‎‎2‎+λt(t为参数)过点(0,-3),‎ ‎∴‎0=2+t,‎‎-3=-‎3‎‎2‎+λt,‎解得t=-2,‎λ=‎3‎‎4‎,‎ ‎∴直线l的方程为3x-4y-12=0.‎ 设与直线l平行且与曲线C2相切的直线方程为3x-4y+m=0,‎ 则圆心C2(4,-3)到直线l的距离d=r,即‎|3×4-4×(-3)+m|‎‎3‎‎2‎‎+‎‎4‎‎2‎=5化为|m+24|=25,解得m=1或-49,‎ ‎∴与直线l平行且与曲线C2相切的直线方程为3x-4y+1=0或3x-4y-49=0.‎ ‎■(2015甘肃省兰州市七里河区一中数学模拟,极坐标方程与参数方程的应用,选择题,理23)已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线L的参数方程为x=1+t,‎y=2+‎3‎t(t为参数).‎ ‎(1)写出直线l的普通方程与Q曲线C的直角坐标方程;‎ ‎(2)设曲线C经过伸缩变换x'=x,‎y'=‎1‎‎2‎y得到曲线C',设M(x,y)为C'上任意一点,求x2-‎3‎xy+2y2的最小值,并求相应的点M的坐标.‎ 解:(1)∵直线l的参数方程为x=1+t,‎y=2+‎3‎t(t为参数),‎ ‎∴消去参数t得直线l的普通方程为‎3‎x-y-‎3‎+2=0,‎ ‎∵ρ=2,∴曲线C的直角坐标方程为x2+y2=4.‎ ‎(2)∵曲线C:x2+y2=4经过伸缩变换x'=x,‎y'=‎1‎‎2‎y得到曲线C',‎ ‎∴C':x‎2‎‎4‎+y2=1,‎ 设M(2cos θ,sin θ),则x=2cos θ,y=sin θ,‎ ‎∴x2-‎3‎xy+2y2=3+2cos‎2θ+‎π‎3‎,‎ ‎∴当θ=π‎3‎+kπ,k∈Z时,即M为‎1,‎‎3‎‎2‎或‎-1,-‎‎3‎‎2‎时,x2-‎3‎xy+2y2的最小值为1.‎ ‎■(2015甘肃省河西三校普通高中高三第一次联考,极坐标方程与参数方程的应用,解答题,理23)以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为‎4,‎π‎2‎.若直线l过点P,且倾斜角为π‎3‎,圆C以M为圆心、4为半径.‎ ‎(1)求直线l的参数方程和圆C的极坐标方程;‎ ‎(2)试判定直线l和圆C的位置关系.‎ 解:(1)直线l的参数方程为x=1+‎1‎‎2‎t,‎y=-5+‎3‎‎2‎t(t为参数).‎ 圆C的极坐标方程为ρ=8sin θ.‎ ‎(2)因为M‎4,‎π‎2‎对应的直角坐标为(0,4),‎ 直线l化为普通方程为‎3‎x-y-5-‎3‎=0.‎ 圆心到直线l的距离d=‎|0-4-5-‎3‎|‎‎3+1‎‎=‎‎9+‎‎3‎‎2‎>4,‎ 所以直线l与圆C相离.‎ ‎14.3不等式选讲 专题3‎ 含绝对值不等式的问题 ‎■(2015甘肃省民乐一中高三第一次诊断考试,含绝对值不等式的问题,解答题,理24)设函数f(x)=|x-a|+3x,其中a>0.‎ ‎(1)当a=1时,求不等式f(x)≥3x+2的解集;‎ ‎(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.‎ 解:(1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.‎ 由此可得x≥3或x≤-1.‎ 故不等式f(x)≥3x+2的解集为{x|x≥3,或x≤-1}.‎ ‎(2)由f(x)≤0,得|x-a|+3x≤0,此不等式化为不等式组x≥a,‎x-a+3x≤0,‎或x≤a,‎a-x+3x≤0,‎即x≥a,‎x≤‎a‎4‎或x≤a,‎x≤-a‎2‎.‎ 因为a>0,所以不等式组的解集为xx≤-‎a‎2‎,由题设可得-a‎2‎=-1,故a=2.‎ ‎■(2015甘肃省白银市会宁二中高考数学模拟,含绝对值不等式的问题,解答题,理24)已知函数f(x)=|x+3|+|x-a|(a>0).‎ ‎(1)当a=4时,已知f(x)=7,求x的取值范围;‎ ‎(2)若f(x)≥6的解集为{x|x≤-4,或x≥2},求a的值.‎ 解:(1)当a=4时,函数f(x)=|x+3|+|x-4|=|x+3|+|4-x|≥|x+3+4-x|=7,‎ 当且仅当(x+3)(4-x)≥0时,即-3≤x≤4时取等号,‎ 故x的取值范围为[-3,4].‎ ‎(2)若f(x)≥6的解集为{x|x≤-4,或x≥2},‎ 则-4和2是方程f(x)=|x+3|+|x-a|=6的两根,‎ 即‎1+|-4-a|=6,‎‎5+|2-a|=6,‎解得a=1.‎ ‎■(2015甘肃省河西三校普通高中高三第一次联考,含绝对值不等式的问题,解答题,理24)已知函数f(x)=|x-1|,g(x)=-|x+3|+a,a∈R.‎ ‎(1)解关于x的不等式g(x)>6;‎ ‎(2)若函数y=2f(x)的图象恒在函数y=g(x)的上方,求实数a的取值范围.‎ 解:(1)不等式即-|x+3|+a>6,即|x+3|6时,得-(a-6)6).‎ ‎(2)y=2f(x)图象恒在g(x)图象上方,故2f(x)-g(x)>0,等价于a<2|x-1|+|x+3|.‎ 设h(x)=2|x-1|+|x+3|=‎‎-3x-1,x≤-3,‎‎5-x,-31.‎ 画出图象可知当x=1时,h(x)取得最小值为4,‎ ‎∴a<4时,函数y=2f(x)的图象恒在函数y=g(x)的上方.‎ 专题4‎ 不等式的证明 ‎■(2015甘肃省兰州市七里河区一中数学模拟,不等式的证明,解答题,理24)已知正数a,b,c满足a+b+c=6,求证:‎1‎a(1+b)‎‎+‎1‎b(1+c)‎+‎1‎c(1+a)‎≥‎‎1‎‎2‎.‎ 证明:由已知及均值不等式:‎‎1‎a(1+b)‎‎+‎1‎b(1+c)‎+‎‎1‎c(1+a)‎ ‎≥‎‎3‎‎3‎abc(1+a)(1+b)(1+c)‎ ‎=‎‎3‎‎3‎abc‎·‎‎3‎‎(1+a)(1+b)(1+c)‎ ‎≥‎‎3‎a+b+c‎3‎‎·‎‎1+a+1+b+1+c‎3‎ ‎=‎3‎‎2×3‎‎=‎‎1‎‎2‎.‎