2021届课标版高考文科数学大一轮复习课件：§5-2 平面向量的数量积及平面向量的应用（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§5-2 平面向量的数量积及平面向量的应用（讲解部分）

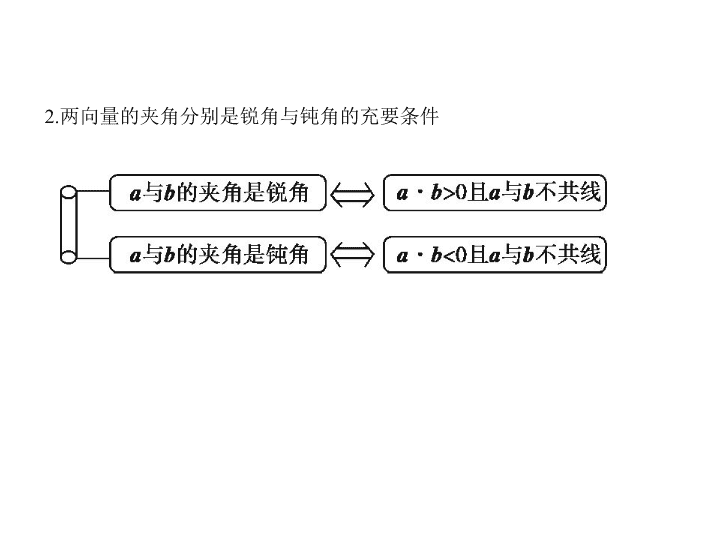
考点一　平面向量的数量积 考点清单 考向基础 1.两向量夹角的定义和范围     2.两向量的夹角分别是锐角与钝角的充要条件 3.平面向量的数量积   4.向量数量积的性质 设 a , b 都是非零向量, e 是与 b 方向相同的单位向量, θ 是 a 与 e 的夹角,则 (1) e · a = a · e = | a |·cos θ . (2)当 a 与 b 同向时, a · b =| a || b | ;当 a 与 b 反向时, a · b =-| a || b | . 特别地, a · a =| a | 2 . (3) | a · b | ≤ | a |·| b | . 5.坐标表示 若 a =( x , y ),则 a · a = a 2 =| a | 2 = x 2 + y 2 ,| a |=   . 考向一　求平面向量的数量积 考向突破 例1　(1)(2020届皖南八校摸底考试,5)已知   =(-3,-2),   =( m ,1),|   |=3,则   ·   =   (　　) A.7　    B.-7　    C.15　    D.-15 (2)(命题标准样题,13)设△ ABC 中 AC =1, AB =2,∠ CAB =60 ° ,   = a ,   = b ,   = c ,则 a · b + b · c + c · a = 　　　     . 解析　(1)   =   -   =( m +3,3),∵|   |=3,∴( m +3) 2 +9=9,∴ m =-3,∴   =(-3, 1),∵   =(3,2),∴   ·   =-9+2=-7. (2)试题考查平面向量的概念、运算、平面向量数量积等数学知识.试题解 法灵活多样,考查化归与转化的数学思想,体现了理性思维的学科素养.考 查了逻辑推理能力、运算求解能力,落实了基础性的考查要求. a · b + b · c + c · a = b ·( a + c )+ c · a =-( a + c ) 2 + c · a =- a 2 - c · a - c 2 =-4. 答案　(1)B　(2)-4 考向二　求平面向量的投影 例2    (2020届贵州遵义摸底考试,6)已知向量 a , b 的夹角为60 ° ,且| a |=| b |=2,则 向量 a - b 在向量 a 方向上的投影为   (　　) A.-1　    B.1　    C.2　    D.3 解析　设向量 a - b 与向量 a 的夹角为 θ ,则向量 a - b 在向量 a 方向上的投影为| a - b |cos θ =| a - b |·   =   =   =   =1,故选B. 答案    B 考点二　平面向量数量积的应用 考向基础 1.向量数量积的应用 已知 a =( x 1 , y 1 ), b =( x 2 , y 2 ). (1)证明垂直问题,常用向量垂直的充要条件, a ⊥ b ⇔ a · b =0 ⇔ x 1 x 2 + y 1 y 2 =0 . (2)求解夹角问题,常利用夹角公式: cos θ =   =   (其中 θ 为 a 与 b 的夹角). (3)求线段长度问题,常利用向量的长度公式: | a |=   =   或|   |=   . 在△ ABC 中,∠ A ,∠ B ,∠ C 所对的边分别为 a , b , c . (1)在   = λ   的条件下,存在 λ 使得 I 为△ ABC 的内心; a   + b   + c   =0 ⇔ P 为△ ABC 的内心. (2)|   |=|   |=|   | ⇔ P 为△ ABC 的外心. (3)   +   +   =0 ⇔ G 为△ ABC 的重心. (4)   ·   =   ·   =   ·   ⇔ P 为△ ABC 的垂心. 2.向量中常用的结论 考向一　求平面向量的夹角 考向突破 例3    (2020届广西桂林十八中8月月考,6)已知向量 a , b 满足| a |=   ,| b |=1,且 | b + a |=2,则向量 a 与 b 的夹角的余弦值为   (　　) A.   　    B.   　    C.   　    D.   解析　由| b + a |=2得( b + a ) 2 =4,即 a 2 +2 a · b + b 2 =4.又∵| a |=   ,| b |=1,∴2+2 a · b +1= 4,解得 a · b =   .设向量 a 与 b 的夹角为 θ ,则有cos θ =   =   =   =   ,故选 D. 答案    D 例4    (2018湖南永州二模,4)已知非零向量 a , b 的夹角为60 ° ,且| b |=1,|2 a - b |= 1,则| a |=   (　　) A.   　    B.1　    C.   　    D.2 考向二　求平面向量的模 解析　∵非零向量 a , b 的夹角为60 ° ,且| b |=1, ∴ a · b =| a | × 1 ×   =   . ∵|2 a - b |=1, ∴|2 a - b | 2 =4 a 2 -4 a · b + b 2 =4| a | 2 -2| a |+1=1, ∴4| a | 2 -2| a |=0, ∴| a |=   (| a |=0舍去),故选A. 答案    A 方法1 　平面向量的模的求解方法 利用向量数量积求解向量的长度问题是向量数量积的重要应用,要掌握此 类问题的处理方法: 1. a 2 = a · a =| a | 2 或 | a |=   . 2.| a ± b |=   =   . 3.若 a =( x , y ),则 | a |=   或| a | 2 = x 2 + y 2 . 方法技巧 例1　已知点 A (4,3)和点 B (1,2),点 O 为坐标原点,则|   + t   |( t ∈R)的最小值 为   (　　) A.5   　    B.5　    C.3　    D.   解析　由题意可得   =(4,3),   =(1,2), ∴   + t   =(4+ t ,3+2 t ), ∴|   + t   |=   =   =   , ∵ t ∈R,∴当 t =-2时,|   + t   |取得最小值   ,故选D. 答案    D 方法2 　平面向量夹角的求解方法 1.定义法:利用向量数量积的定义知,cos θ =   ,其中两个向量的夹角θ∈ [0,π],求解时应求出三个量: a · b ,| a |,| b |或找出这三个量之间的关系. 2.坐标法:若 a =( x 1 , y 1 ), b =( x 2 , y 2 ), θ 为 a , b 的夹角,则cos θ =   . 3.三角函数法:可以把所求两向量的夹角放到三角形中,利用正、余弦定理 和三角形的面积公式等知识进行求解. 例2    (2020届江西南昌三校期初调研,6)若非零向量 a , b 满足| a |=   | b |,且 ( a - b )⊥(3 a +2 b ),则 a 与 b 的夹角为   (　　) A.   　    B.   　    C.   　    D.π 解析　由( a - b )⊥(3 a +2 b ),得( a - b )·(3 a +2 b )=0, 即3 a 2 - a · b -2 b 2 =0,又知| a |=   | b |, ∴ a · b =3 a 2 -2 b 2 =3 ×   | b | 2 -2| b | 2 =   | b | 2 . 设 a 与 b 的夹角为 θ ,则cos θ =   =   =   , 又知 θ ∈[0,π],∴ θ =   ,即 a 与 b 的夹角为   . 答案    A 方法3 　用向量法解决平面几何问题 1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系, 用向量表示问题中涉及的几何元素,将平面几何问题转化为向量的问题; ②通过向量运算研究几何元素之间的关系,如距离、夹角等问题;③把运算 结果转化成几何关系. 2.用向量法解平面几何问题,主要是 通过建立平面直角坐标系将问题坐标 化, 然后利用平面向量的坐标运算求解有关问题,这样可以避免繁杂的逻辑 推理,同时加强了数形结合思想在解题中的应用. 例3　在平行四边形 ABCD 中, AD =1,∠ BAD =60 ° , E 为 CD 的中点.若   ·   = 1,则 AB 的长为 　　　     . 解析　解法一:由题意可知,   =   +   ,   =-     +   . 因为   ·   =1,所以(   +   )·   =1, 即   +     ·   -     =1.   ① 因为|   |=1,∠ BAD =60 ° , 所以   ·   =   |   |, 因此①式可化为1+   |   |-   |   | 2 =1. 解得|   |=0(舍去)或|   |=   , 所以 AB 的长为   . 解法二:以 A 为原点, AB 所在直线为 x 轴建立如图所示的直角坐标系,过 D 作 DM ⊥ AB 于点 M . 由 AD =1,∠ BAD =60 ° ,可知 AM =   , DM =   , ∴ D   . 设|   |= m ( m >0),则 B ( m ,0), C   , 因为 E 是 CD 的中点,所以 E   . 所以   =   ,   =   .   由   ·   =1可得     +   =1, 即2 m 2 - m =0,所以 m =0(舍去)或 m =   . 故 AB 的长为   . 答案