新课标人教版2013届高三物理总复习一轮课时作业11

新课标人教版2013届高三物理总复习一轮课时作业11

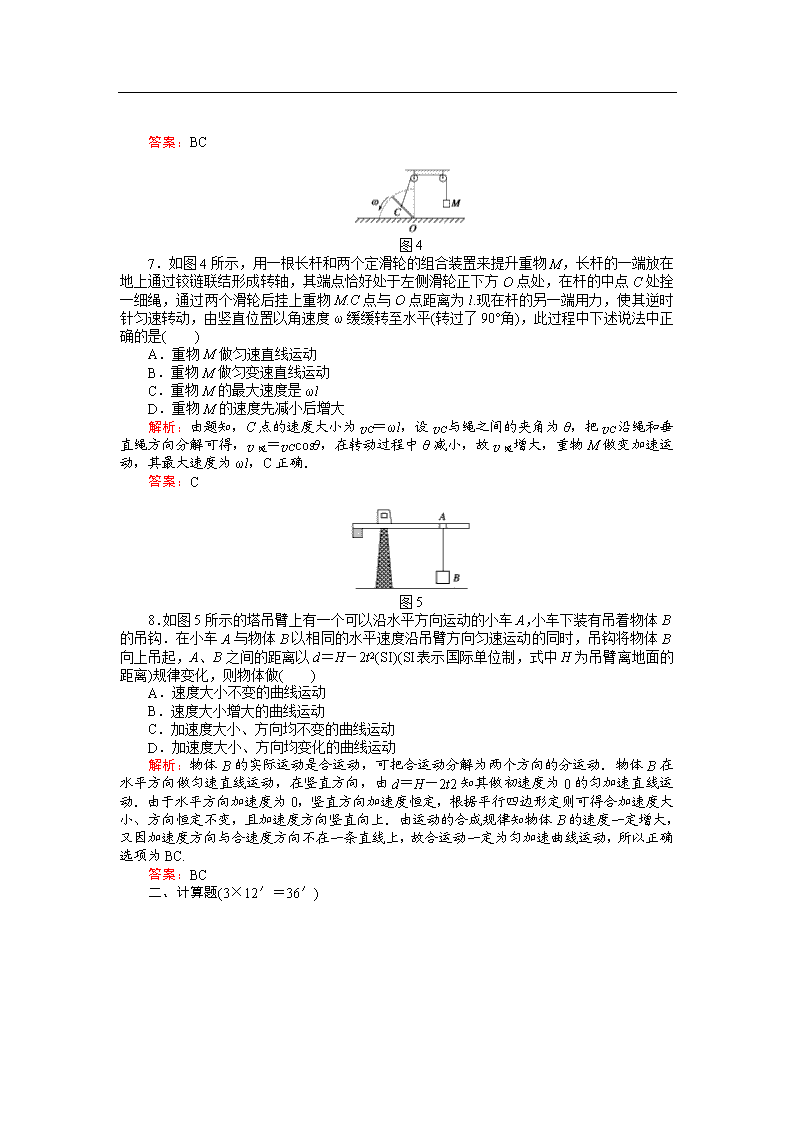
新课标人教版2013届高三物理总复习一轮课时作业 课时作业11　运动的合成与分解 时间：45分钟　　满分：100分 一、选择题(8×8′＝64′)‎ ‎1．下列说法正确的是 (　　)‎ A．物体在恒力作用下不可能做曲线运动 B．物体在变力作用下有可能做曲线运动 C．物体做曲线运动，沿垂直速度方向的合力一定不为零 D．沿垂直速度方向的合力为零时，物体一定做直线运动 解析：物体是否做曲线运动，取决于物体所受合外力方向与物体运动方向是否共线，只要两者不共线，无论物体所受合外力是恒力还是变力，物体都做曲线运动，故A错误，B正确．由垂直速度方向的力改变速度的方向，沿速度方向的力改变速度的大小知，C、D正确．‎ 答案：BCD ‎2．某一物体受到几个共点力的作用而处于平衡状态，当撤去某个恒力F1时，物体可能做 (　　)‎ A．匀加速直线运动　　　　 B．匀减速直线运动 C．匀变速曲线运动 D．变加速曲线运动 解析：由于撤去恒力F1后物体受的合力为恒力，故一定是匀变速运动，但初速度的方向不知，所以轨迹可能是直线也可能是曲线，也可能是匀加速直线运动，也可能是匀减速直线运动．故ABC都是有可能的．‎ 答案：ABC ‎3．在地面上观察下列物体的运动，其中物体一定做曲线运动的是 (　　)‎ A．向东运动的质点受到一个向西的力的作用 B．正在竖直上升的气球突然遭遇一阵北风 C．河水匀速流动，正在河里匀速驶向对岸的汽艇 D．在匀速行驶的列车上，相对列车水平向后抛出的一个小球 解析：A：质点仍做直线运动；‎ B：气球的运动方向与受力方向不共线，做曲线运动；‎ C：两个匀速直线运动的合运动仍是匀速直线运动；‎ D：若小球相对车向后抛出的速度与车前进速度大小相同，则小球相对地面的速度为零，故做自由落体运动，为直线运动．‎ 答案：B 图1‎ ‎4．一质点在xOy平面内的运动轨迹如图1，下列判断正确的是 (　　)‎ A．若x方向始终匀速，则y方向先加速后减速 B．若x方向始终匀速，则y方向先减速后加速 C．若y方向始终匀速，则x方向先减速后加速 D．若y方向始终匀速，则x方向先加速后减速 解析：在x方向，质点若始终匀速，则表明质点受到的合外力沿y方向，由于做曲线运动的轨迹偏向合外力的方向，所以合外力是先沿y轴的反方向，再沿y轴的正方向，也就是说先是与y轴上的分速度方向相反，后是相同，所以沿y轴先减速后加速，B对；同理可得，在y方向，质点若始终匀速，应是沿x方向先加速后减速，D对．‎ 答案：BD ‎5．一快艇要从岸边某处到达河中离岸‎100 m远的浮标处，已知快艇在静水中的速度图象如图2甲，流水的速度图象如图2乙，假设行驶中快艇在静水中航行的分速度方向选定后就不再改变，则 (　　)‎ 图2‎ A．快艇的运动轨迹可能是直线 B．快艇的运动轨迹只可能是曲线 C．最快达到浮标处通过的位移为‎100 m D．最快达到浮标处所用时间为20 s 解析：艇的速度为艇在静水中的速度与水速的合速度．由图知艇的静水速度为匀加速，水速为匀速，故快艇必做曲线运动，B项正确．当船头与河岸垂直时，到达浮标处时间最短，而此时船做曲线运动，故位移大于100 m，C项错误．最快的时间由100＝at2，其中a＝0.5 m/s2，可以求出最短时间为20 s，D项正确．‎ 答案：BD ‎6．民族运动会上有一骑射项目，运动员骑在奔跑的马背上，弯弓放箭射击侧向的固定目标假设运动员骑马奔驰的速度为v1，运动员静止时射出的弓箭速度为v2，跑道离固定目标的最近距离为d.要想命中目标且射出的箭在空中飞行时间最短，则 (　　)‎ A．运动员放箭处离目标的距离为 B．运动员放箭处离目标的距离为 图3‎ C．箭射到靶的最短时间为 D．箭射到靶的最短时间为 解析：要想在最短时间内射中目标，箭垂直于跑道射出时间t＝，运动员放箭时应使箭的合速度方向对准目标，如图3，则有s＝vt＝·.‎ 答案：BC 图4‎ ‎7．如图4所示，用一根长杆和两个定滑轮的组合装置来提升重物M，长杆的一端放在地上通过铰链联结形成转轴，其端点恰好处于左侧滑轮正下方O点处，在杆的中点C处拴一细绳，通过两个滑轮后挂上重物M.C点与O点距离为l.现在杆的另一端用力，使其逆时针匀速转动，由竖直位置以角速度ω缓缓转至水平(转过了90°角)，此过程中下述说法中正确的是(　　)‎ A．重物M做匀速直线运动 B．重物M做匀变速直线运动 C．重物M的最大速度是ωl D．重物M的速度先减小后增大 解析：由题知，C点的速度大小为vC＝ωl，设vC与绳之间的夹角为θ，把vC沿绳和垂直绳方向分解可得，v绳＝vCcosθ，在转动过程中θ减小，故v绳增大，重物M做变加速运动，其最大速度为ωl，C正确．‎ 答案：C 图5‎ ‎8．如图5所示的塔吊臂上有一个可以沿水平方向运动的小车A，小车下装有吊着物体B的吊钩．在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时，吊钩将物体B向上吊起，A、B之间的距离以d＝H－2t2(SI)(SI表示国际单位制，式中H为吊臂离地面的距离)规律变化，则物体做(　　)‎ A．速度大小不变的曲线运动 B．速度大小增大的曲线运动 C．加速度大小、方向均不变的曲线运动 D．加速度大小、方向均变化的曲线运动 解析：物体B的实际运动是合运动，可把合运动分解为两个方向的分运动．物体B在水平方向做匀速直线运动，在竖直方向，由d＝H－2t2知其做初速度为0的匀加速直线运动．由于水平方向加速度为0，竖直方向加速度恒定，根据平行四边形定则可得合加速度大小、方向恒定不变，且加速度方向竖直向上．由运动的合成规律知物体B的速度一定增大，又因加速度方向与合速度方向不在一条直线上，故合运动一定为匀加速曲线运动，所以正确选项为BC.‎ 答案：BC 二、计算题(3×12′＝36′)‎ 图6‎ ‎9．北风速度为‎4 m/s，大河中的水流正以‎3 m/s的速度向东流动，船上的乘客看见轮船烟囱冒出的烟柱是竖直的，求轮船相对于水的航行速度多大？什么方向？‎ 解析：轮船的实际航向为正南，大小为4 m/s时，才能看见烟柱竖直．由于河水流动，轮船应该有一个分速度：大小与v水相等，方向与v水相反，这样轮船才会朝正南方向行驶，如图6所示．tanθ＝＝，则θ＝37°.即船头应该与上游河岸成53°角向南航行．且v船＝＝ m/s＝5 m/s.‎ 图7‎ ‎10．如图7所示，已知h＝‎2 m．小船以v＝‎4 m/s的速度匀速向左运动，并拉动岸上的车，当船经图中的A点时，绳与水平方向的夹角为θ＝60°，当船经过图中B点时，绳子与水平方向的夹角θ′＝30°，求该过程车的速度变化了多少？‎ 图8‎ 解析：小船的实际运动可分解为两个分运动，一方面船绕O点做圆周运动，因此有垂直于绳斜向上的分速度v1，另一方面是沿绳子方向的运动，因此有分速度v2.如图8所示，当车经A点时由几何知识知v2＝v·cosθ＝＝2 m/s.又因绳的长度不变，所以v车＝v2＝2 m/s.同理，当车经B点时，v车′＝v2′＝vcosθ′＝2 m/s，所以从A到B的过程中车的速度增加了Δv＝v车′－v车＝1.46 m/s.‎ 图9‎ ‎11．如图9所示，货车正在以a＝‎0.1 m/s2的加速度启动，同时，一只壁虎以v2＝‎0.2 m/s的速度在货车壁上向上匀速爬行．试求：‎ ‎(1)经过2 s时，地面上的人看到壁虎的速度大小和方向；‎ ‎(2)经过2 s时壁虎相对于地面发生的位移；‎ ‎(3)在地面上观察壁虎做直线运动还是曲线运动？‎ 解析：(1)壁虎同时参与了相对于车向上的匀速运动和随车一起向左的匀加速直线运动．经过2 s时，壁虎向上运动的速度vy＝v2＝0.2 m/s，随车运动的速度vx＝v1＝at＝0.2 m/s，如图10(甲)所示，壁虎运动的合速度在t＝2 s末，大小为v＝＝ m/s＝0.28 m/s，tanα＝＝＝1，壁虎的速度方向在该时刻与水平方向成45°角．‎ 图10‎ ‎(2)如图10(乙)所示，在汽车启动后2 s这段时间内，壁虎的水平位移x＝at2＝‎0.2 m，竖直位移y＝v2t＝‎0.4 m，壁虎相对地面发生的位移s＝＝‎0.45 m，与水平方向所成的角θ＝arctan＝arctan2.‎ ‎(3)由上面分析知x＝at2＝0.05t2，y＝0.2t，消去时间t，得x＝1.25y2，是一条如图10(丙)所示的抛物线(以壁虎刚开始爬动处为坐标原点，壁虎爬行的方向为y轴正方向，车前进的方向为x轴正方向)，所以壁虎做曲线运动，或者用初速度方向与加速度方向垂直的关系，也可以判断出壁虎的运动轨迹是曲线．‎