- 2021-06-02 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册 第13章 轴对称 13.2 作轴对称图形 (1)
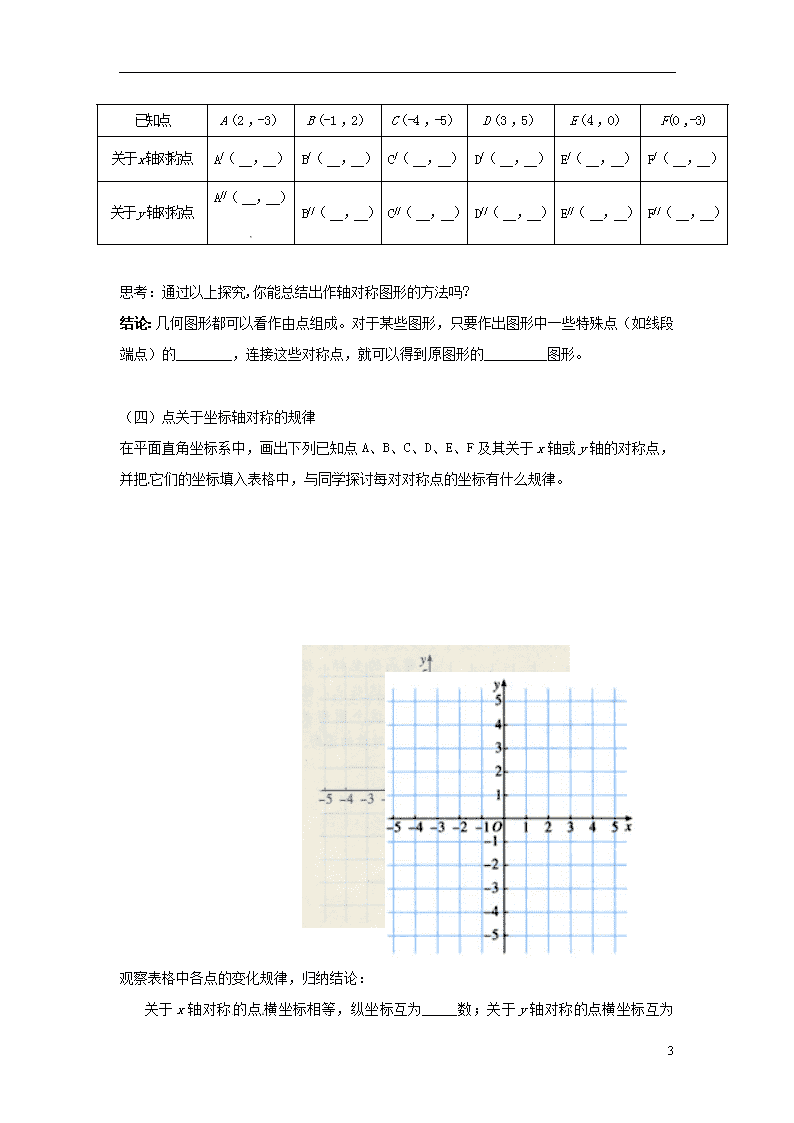
课题:13.2 作轴对称图形 (1) 【学习目标】 1、能作轴对称图形,能应用轴对称进行简单的图案设计,能用轴对称的知识解决相应的数学问题,初步掌握一个点关于x轴或y轴对称的点的坐标变化规律。 2、通过独立思考、交流讨论、展示质疑,发展观察、归纳、想象及推理能力。 3、极度热情、享受成功、感受数学就在身边。 【学习重难点】 重点:作轴对称图形 难点:用轴对称知识解决相应的数学问题。 一、知识链接 复习旧知:1.线段公理:两点之间______最短 2.垂直平分线的性质:如果某个图形关于_____________对称,那么对称轴是任何一对对应点所连_______的垂直平分线。 自主学习(新知):精读课本第67-68页,用红色的笔对有关概念进行勾画并找出自己的疑惑和要讨论的问题,准备在课堂上讨论质疑。 思考:自己动手在一张半透明的纸的左边部份画一个图案,将这张纸对折后描图,再打开纸,看看你得到了什么?改变折痕的位置并重复几次,你又得到了什么? 结论: 1、 由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的_______、________完全相同; 2、 新图形上的每一个点都是原图形上的某一点关于直线l的________点; 3、 连接任意一对_______点的线段被对称轴________平分; 4、 对称轴方向和位置发生变化时,得到图形的_______和_________也发生变化。 二、合作与探究 l A. (一)作出点A关于 l 的对称点A’ 作法: 1、 过点A作l的____线,垂足为_____; 2、 在_____线上截取_____=_______; 10 1、 点______就是点A关于直线l的对称点。 l A B l A B (二)作出线段AB关于直线 l成轴对称的图形 l A B l A B (三)作一图形关于某直线对称的图形(3种情况) l A B C (1)第一种情况(图形在对称轴同一侧):课本67页例1 如图(1),已知△ABC和直线l,画出△ABC关于直线l对称的图形。 作法: 1. 过点A作l的____线,垂足为_____;在_____线上 截取____=____;点___就是点A关于直线l的对称点. 2.同理,分别作出点B、C关于直线l的对称点 、 3.连接 、 、 ,则△A′B′C′即为所求. (2)第二种情况(图形有一顶点在对称轴上): 如图(2), 已知△ABC和直线l,画出△ABC关于直线l对称的图形。 (3)第三种情况(图形在对称轴两侧): 如图(3), 已知△ABC和直线l,画出△ABC关于直线l对称的图形。 10 思考:通过以上探究,你能总结出作轴对称图形的方法吗? 结论:几何图形都可以看作由点组成。对于某些图形,只要作出图形中一些特殊点(如线段端点)的________,连接这些对称点,就可以得到原图形的_________图形。 (四)点关于坐标轴对称的规律 在平面直角坐标系中,画出下列已知点A、B、C、D、E、F及其关于x轴或y轴的对称点,并把它们的坐标填入表格中,与同学探讨每对对称点的坐标有什么规律。 已知点 A(2 ,-3) B(-1 ,2) C(-4 ,-5) D(3 ,5) E(4 ,0) F(0 ,-3) 关于x轴对称点 A/( , ) B/( , ) C/( , ) D/( , ) E/( , ) F/( , ) 关于y 轴对称点 A//( , ) B//( , ) C//( , ) D//( , ) E//( , ) F//( , ) 观察表格中各点的变化规律,归纳结论: 关于x轴对称的点横坐标相等,纵坐标互为_____数;关于y 10 轴对称的点横坐标互为_____数,纵坐标相等。 即:点P(x, y)关于x轴对称的点的坐标为(______,_____); 点P(x, y)关于y轴对称的点的坐标为(______,_____)。 三、巩固练习 l l l l 基础练习: 1、把下列各图补成以 l为对称轴的轴对称图形。 2、 用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部份能够重合,哪些部份不能重合。 3、 如下图1作五角星关于与某条直线对称的图形时,最多要选_______个关键点。 图1 图2 4、如上图2,一轴对称图形画出了它的一半,请你以点画线为对称轴画出它的另一半 5、写出下列各点关于x轴和y轴对称的点的坐标: A(2,-3);B(-1 ,2);C(-6 ,-5);D(0,-1.6); E(4 ,0) 各点关于x轴对称点的坐标: A1( , )、B1( , )、C1( , )、D1( , )、E1( , ) 各点关于y轴对称的点坐标: A2( , )、B2( , )、C2( , )、D2( , )、E2( , ) 10 6.如图,△ABO关于x轴对称,点A的坐标为(1 ,-2),写出点B的坐标。 三、要点归纳 1.画出点A关于 l 的对称点A’(作法) 2. 作出与线段AB关于直线 l成轴对称的图形 3. 作一图形关于某直线对称的图形的关键是什么? 4.点P(x, y)关于x轴对称的点的坐标为(______,_____); 点P(x, y)关于y轴对称的点的坐标为(______,_____)。 课后反思: . . (实际 课时) 课题:13.2.2 作轴对称图形 (2) 【学习目标】 1、加深掌握一个点关于x轴或y轴对称的点的坐标变化规律,并能利用这种坐标的变化规律在平面直角坐标系中作出一个图形关于x轴或y轴对称的图形。 2、培养探索问题的能力, 发展数形结合的思维意识。 【学习重难点】 重点:理解图形上的点的坐标的变化与图形的轴对称变换之间的关系;在用坐标表示轴对称时发展形象思维能力和数形结合的意识。 难点:用坐标表示轴对称。 10 一、 知识链接 复习旧知: 1.由一个平面图形得到它的轴对称的图形叫做轴对称变换,轴对称变换不会改变图形的_______和________,只会改变图形_________。 2. 点(1 , 0),(2 , -3),(-1 ,2 )关于x轴对称的点的坐标 分别是(____,____); (_____,_____);(_____,____); 点(0 ,-3),(-2 , 3),(1 ,-2)关于y轴对称的点的坐标 分别是(____,____);(____,____);(_____,_____)。 自主学习(新知):精读课本第69-70页,用红色的笔对有关概念进行勾画并找出自己的疑惑和要讨论的问题,准备在课堂上讨论质疑。 二、合作与探究 (一) 作一图形关于坐标轴对称 (课本70页例2) 如图, 四边形ABCD的四个顶点的坐标分别为A(-5 ,1)、B(-2 ,1)、 C(-2 ,5)、 D(-5 ,4),分别作出四边形关于x轴与y轴对称的图形。 A B C D 作法归纳:1.求出对称点的 2.描点3.连线 (三)在平面直角坐标系中画出下列已知点的对称点,并把坐标填入表格中 已 知 点 A(2,3) B(-1,5) C(4,-2) D(0,3) E(-2,-3) 关于一三象限角平分线对称的点 ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) 10 关于二四象限角平分线对称的点 观察表格中各点的变化规律,归纳结论: 关于一,三象限角平分线对称的两点,它们的坐标有如下特征: 其中一个点的横坐标与纵坐标分别是另一个点的____坐标与____坐标; 关于第二、第四象限角平分线对称的两点其中一个点的横、纵坐标另 一个点的____坐标的相反数与____坐标的相反数。 即:点(x, y)关于一,三象限角平分线对称的点的坐标为(______,_____); 点(x, y)关于二、四象限角平分线对称的点的坐标为(______,_____)。 10 三、巩固练习 基础练习: 1、 (1)观察右图中两个圆脸有什么关系? ____________________________________________ (2)已知右边圆脸右眼B的坐标为(4,3), 左眼A的坐标为(2,3),嘴角两个端点,右端点C 的坐标为(4,1),左端点D的坐标为(2,1)。 请根据图形写出左边圆脸上左眼,右眼及嘴角两端点 的坐标A1____________;B1______________; C1_____________; D1_____________ (3) A与A1、B与B1、C与C1、D与D1分别关于_________对称。 2、已知点与点 (1)若点与点关于x轴对称,则=_____ =_______。 (2)若点与点关于y轴对称,则 =_____ =_______。 3、已知点A(2m+1,m-3)关于y轴的对称点在第四象限,则m的取值范围是 。 4、如图,利用关于坐标轴对称的点的坐标特点,分别作出△ABC关于x轴和y轴对称的图形. 10 拓展提升: 1.若,点A关于x轴对称的点为B,点B关于y轴对称的点为C,则点C的坐标是_____________。 2.(1) 分别作出点△ABC关于直线x =1和直线y =-1对称的图形。 (2)你能发现它们的对应点的坐标之间分别有什么关系吗? 根据以上,你能否归纳出下面的规律? (1) 点(x, y)关于直线x=m对称点的坐标是(_______,y)。 10 (2) 点(x, y)关于直线y=n对称点的坐标是(x,_______)。 四、要点归纳 1. 点(x, y)关于x轴对称的点的坐标为(______,_____); 点(x, y)关于y轴对称的点的坐标为(______,_____)。 2. 作一图形关于x轴(或y轴)的对称图形的步骤: (1)求出对称点的 (2) (3)连线 课后反思: . . (实际 课时) 10查看更多