- 2021-06-02 发布 |
- 37.5 KB |
- 8页


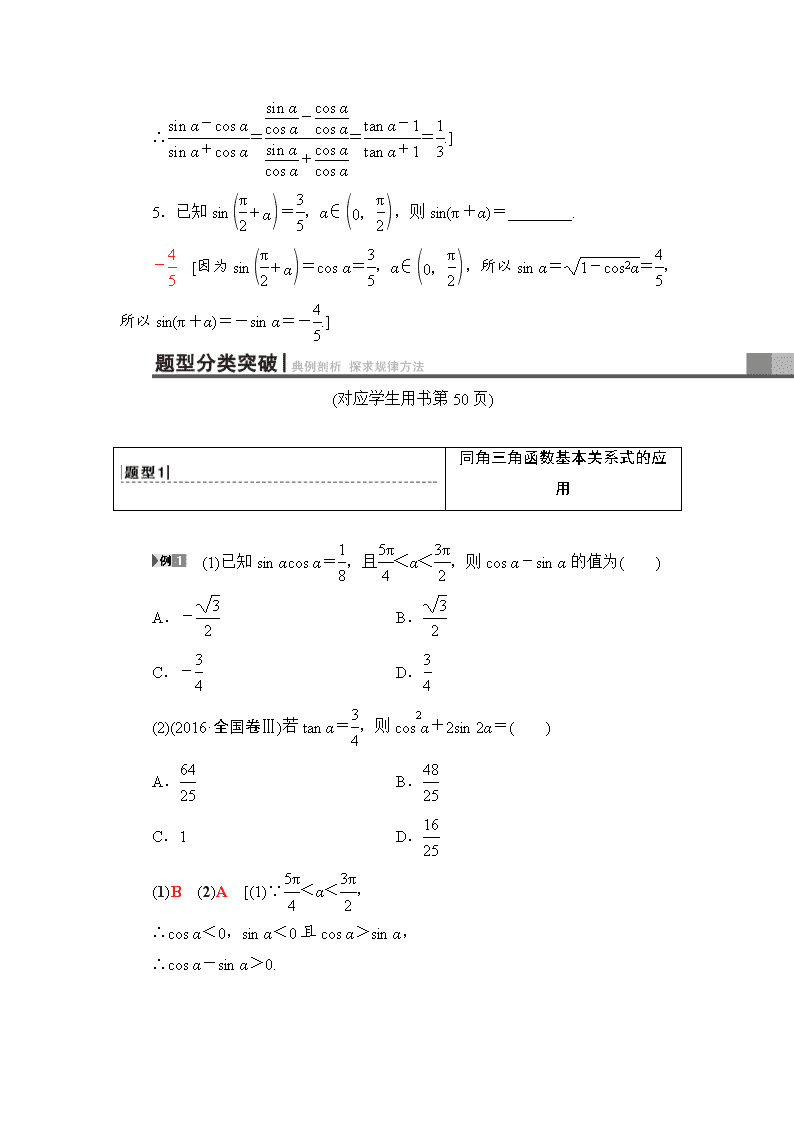
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教A版理第3章第2节 同角三角函数的基本关系与诱导公式教案
第二节 同角三角函数的基本关系与诱导公式 [考纲传真] (教师用书独具)1.理解同角三角函数的基本关系式:sinα+cosα=1,=tan α.2.能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式. (对应学生用书第49页) [基础知识填充] 1.同角三角函数的基本关系式 (1)平方关系:sinα+cosα=1; (2)商数关系:tan α=. 2.诱导公式 组序 一 二 三 四 五 六 角 2kπ+α(k∈Z) π+α -α π-α -α +α 正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan α tan α -tan α -tan α 口诀 函数名不变,符号看象限 函数名改变 符号看象限 记忆规律 奇变偶不变,符号看象限 [知识拓展] 1.诱导公式的两个应用:①求值:负化正,大化小,化到锐角为终了. ②化简:统一角,统一名,同角名少为终了. 2.“1”代换sinα+cosα=1. [基本能力自测] 1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)若α,β为锐角,则sinα+cosβ=1.( ) (2)若α∈R,则tan α=恒成立.( ) (3)sin(π+α)=-sin α成立的条件是α为锐角.( ) (4)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的“奇、偶”是指的奇数倍、偶数倍,“变与不变”指函数名称是否变化.( ) [答案] (1)× (2)× (3)× (4)√ 2.(教材改编)已知α是第二象限角,sin α=,则cos α等于( ) A.- B.- C. D. B [∵sin α=,α是第二象限角, ∴cos α=-=-.] 3.cos-sin=________. [cos-sin=cos+sin=cos+sin =cos +sin =+=.] 4.已知tan α=2,则的值为________. [∵tan α=2, ∴===.] 5.已知sin=,α∈,则sin(π+α)=________. - [因为sin=cos α=,α∈,所以sin α==,所以sin(π+α)=-sin α=-.] (对应学生用书第50页) 同角三角函数基本关系式的应用 (1)已知sin αcos α=,且<α<,则cos α-sin α的值为( ) A.- B. C.- D. (2)(2016·全国卷Ⅲ)若tan α=,则cosα+2sin 2α=( ) A. B. C.1 D. (1)B (2)A [(1)∵<α<, ∴cos α<0,sin α<0且cos α>sin α, ∴cos α-sin α>0. 又(cos α-sin α)=1-2sin αcos α=1-2×=, ∴cos α-sin α=. (2)∵tan α=,则cosα+2sin 2α==== ,故选A.] [规律方法] 同角三角函数关系式及变形公式的应用方法 (1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用f(sin α cos α)=tan α可以实现角α的弦切互化. (2)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二. (3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α. [跟踪训练] (1)若sin α=-,且α为第四象限角,则tan α的值等于( ) 【导学号:97190105】 A. B.- C. D.- (2)已知sin θ+cos θ=,θ∈,则sin θ-cos θ的值为( ) A. B.- C. D.- (1)D (2)B [(1)法一:因为α为第四象限的角,故cos α===, 所以tan α===-. 法二:因为α是第四象限角,且sin α=-,所以可在α的终边上取一点P(12,-5),则tan α==-.故选D. (2)因为(sin θ+cos θ)=sinθ+cosθ+2sin θ·cos θ=1+2sin θcos θ=,所以2sin θcos θ=,则(sin θ-cos θ)=sinθ+cosθ-2sin θ·cos θ=1-2sin θcos θ=.又因为θ∈,所以sin θ<cos θ, 即sin θ-cos θ<0, 所以sin θ-cos θ=-.] 诱导公式的应用 (1)化简sin(-1 071°)sin 99°+sin (-171°)·sin(-261°)的结果为( ) A.1 B.-1 C.0 D.2 (2)已知A=+(k∈Z),则A的值构成的集合是( ) A.{1,-1,2,-2} .{-1,1} C.{2,-2} .{1,-1,0,2,-2} (1)C (2)C [(1)原式=(-sin 1 071°)·sin 99°+sin 171°·sin 261° =-sin(3×360°-9°)sin(90°+9°)+sin(180°-9°)·sin(270°-9°)=sin 9°cos 9°-sin 9°cos 9°=0. (2)当k为偶数时,A=+=2; k为奇数时,A=-=-2.] [规律方法] 利用诱导公式的方法与步骤 (1)方法:利用诱导公式应注意已知角或函数名称与所求角或函数名称之间存在的关系,尤其是角之间的互余、互补关系,选择恰当的公式,向所求角和三角函数进行化归. (2)步骤: 易错警示:利用诱导公式的关键是符号问题. [跟踪训练] (1)(2018·南昌一模)(1)若sin=,则cos=________. (2)计算:=________. (1) (2)-1 [cos=cos=sin=. (2)原式= == =-=-·=-1.] 同角关系式与诱导公式的综合应用 (1)(2016·全国卷Ⅰ)已知θ是第四象限角,且sin=,则tan=________. (2)(2017·郑州质检)已知cos=2sin,则的值为________. 【导学号:97190106】 (1)- (2) [(1)由题意知sin=,θ是第四象限角,所以cos >0,所以cos==. sin=sin=cos=, cos=cos=sin=. ∴tan=-tan-. (2)∵cos=2sin, ∴-sin α=-2cos α, 则sin α=2cos α, 代入sinα+cosα=1, 得cosα=. = ==cosα-=.] [规律方法] 三角函数求值与化简的常用方法 (1)弦切互化法:主要利用公式tan α=进行弦切互化. (2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (3)巧用“1”的变换:1=sin2θ+cos2θ=cos2θ(1+tan2θ)=等. (4)利用相关角的互补、互余等特殊关系可简化解题步骤. [跟踪训练] (1)已知sin α=,α是第二象限角,则tan(π-α)=________. (2)(2018·湖北调考)已知tan=5,则=( ) A. B.- C.± D.- (1) (2)B [(1)∵sin α=,α是第二象限角, ∴cos α=-, ∴tan α=-, 故tan(π-α)=-tan α=. (2)∵tan===-=5, ∴tan x=-, ∴===-,故选B.]查看更多