- 2021-06-02 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】安徽省安庆市怀宁县第二中学2019-2020学年高二下学期期中线上检测(文)
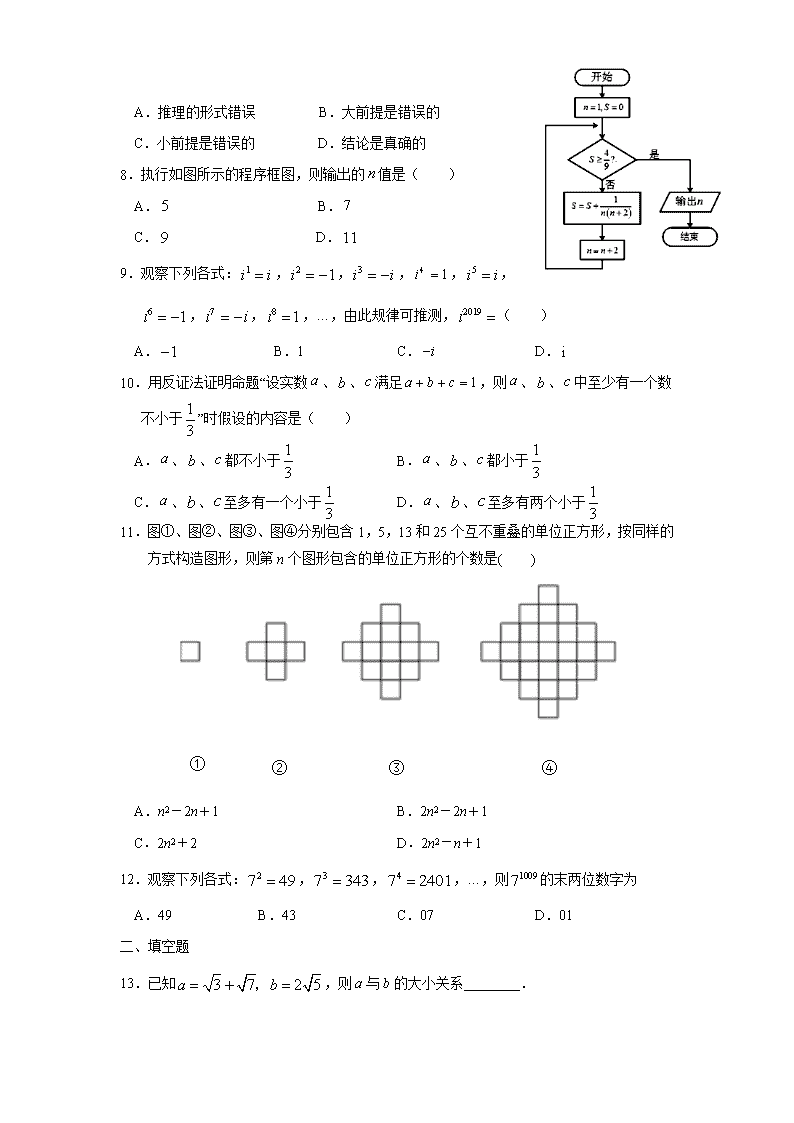
安徽省安庆市怀宁县第二中学2019-2020学年 高二下学期期中线上检测(文) 一、选择题(本大题共12小题,每小题5分,满分60分。) 1.已知复数z=(a2-1)+(a-1)i(a∈R)是纯虚数,则a=( ) A.0 B.1 C.-1 D.±1 2.对两个变量和进行回归分析,得到一组样本数据,则下列说法中不正确的是( ) A.由样本数据得到的回归方程必过样本点的中心 B.残差平方和越小的模型,拟合的效果越好 C.用相关指数来刻画回归效果,越小说明拟合效果越好 D.若变量和之间的相关系数为,则变量和之间具有线性相关关系 3.若复数z满足,则( ) A. B. C. D. 4.已知复数(其中为虚数单位),则复数在坐标平面内对应的点在 A.第一象限 B.第二象限 C.第三象限 D.第四象限 5.若复数满足,则的虚部为( ) A. B. C. D.4 6.已知,,若,则( ) A. B. C. D. 7.指数函数是增函数,而是指数函数,所以是增函数,关于上面推理正确的说法是( ) A.推理的形式错误 B.大前提是错误的 C.小前提是错误的 D.结论是真确的 8.执行如图所示的程序框图,则输出的值是( ) A. B. C. D. 9.观察下列各式:,,,,,,,,…,由此规律可推测,( ) A. B.1 C. D. 10.用反证法证明命题“设实数、、满足,则、、中至少有一个数不小于”时假设的内容是( ) A.、、都不小于 B.、、都小于 C.、、至多有一个小于 D.、、至多有两个小于 11.图①、图②、图③、图④分别包含1,5,13和25个互不重叠的单位正方形,按同样的方式构造图形,则第n个图形包含的单位正方形的个数是( ) ④ ③ ② ① A.n2-2n+1 B.2n2-2n+1 C.2n2+2 D.2n2-n+1 12.观察下列各式:,,,…,则的末两位数字为 A.49 B.43 C.07 D.01 二、填空题 13.已知,则a与b的大小关系________. 14.函数的值域是______________ 15.在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是____________. 16.已知下面五个命题: ①归纳推理是由部分到整体的推理; ②归纳推理是由一般到一般的推理; ③演绎推理是由一般到特殊的推理; ④类比推理是由特殊到一般的推理; ⑤类比推理是由特殊到特殊的推理. 表述正确的是 __ . 三、解答题 17.某班的行政结构如下:班主任下设班委会和团支部,班委会设班长一名,管理学习委员、生活委员、劳动卫生委员、文娱委员和体育委员,团支部设团支书一名,管理组织委员和宣传委员.试画出该班的组织结构图. 18.(1)当时,求的最大值 (2)若x>0,y>0且,求x+y的最小值 19.已知复数 ,则当实数m为何值时,复数z是: (1)实数; (2)虚数; (3)纯虚数; (4)对应的点在第三象限. 20.为了研究某种细菌在特定条件下随时间变化的繁殖情况,得到如下所示实验数据,若与线性相关. 天数(天) 3 4 5 6 7 繁殖个数(千个) 5 6 8 9 12 (1)求关于的回归直线方程; (2)预测时细菌繁殖的个数. (参考公式:,) 21.设,且,,,用反证法证明:至少有一个大于. 22.某知名电商在双十一购物狂欢节中成交额再创新高,月日单日成交额达亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的 位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图: “购物评价为满意”的年龄层次频数分布表: 年龄(岁) 频数 (1)估计参与此次活动的买家的平均年龄(同一组中的数据用该组区间的中点值做代表); (2)若年龄在岁以下的称为“青年买家”,年龄在岁以上(含岁)的称为“中年买家”,完成下面的列联表,并判断能否有的把握认为中、青年买家对此次活动的评价有差异? 评价满意 评价不满意 合计 中年买家 青年买家 合计 附:参考公式:. 参考答案 1—5、CCDDC 6—10、BBCC B 11—12、BC 13.a<b 14.]. 15.甲 16.① ③ ⑤ 17.【答案】见解析 详解:该班的组织结构图如图: 18.(1) (2) ∴x+y最小值为16 19.(1)m=3或m=﹣2;(2)m≠﹣2,m≠3;(3);(4) 【详解】 (1)令 ⇒ m =3或m=﹣2,即m=3或m=﹣2时,z为 实数; (2)可得m≠﹣2,m≠3时复数是虚数. (3);所以复数是纯虚数. (4)若z所对应点在第三象限则 . 20.(1)(2) 试题解析:解:(1)由已知,则, 所以, 所以关于的回归直线方程 (2)当时,(千个) 21.见证明 【详解】证明:(反证法) 假设结论不成立,即, 而 这与相矛盾 故至少有一个大于. 22.【答案】(1)岁(2)列联表见解析,没有 【详解】(1)各年龄段区间,,,,对应的频率分别为,,,,, 所以估计参与此次活动的买家的平均年龄为岁. (2)列联表如下: 评价满意 评价不满意 合计 中年买家 青年买家 合计 由表中数据计算得:,所以没有的把握认为中、青年买家对此次活动的评价有差异.查看更多