- 2021-06-02 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第三章 指数函数与对数函数小结与复习教案 北师大版必修1
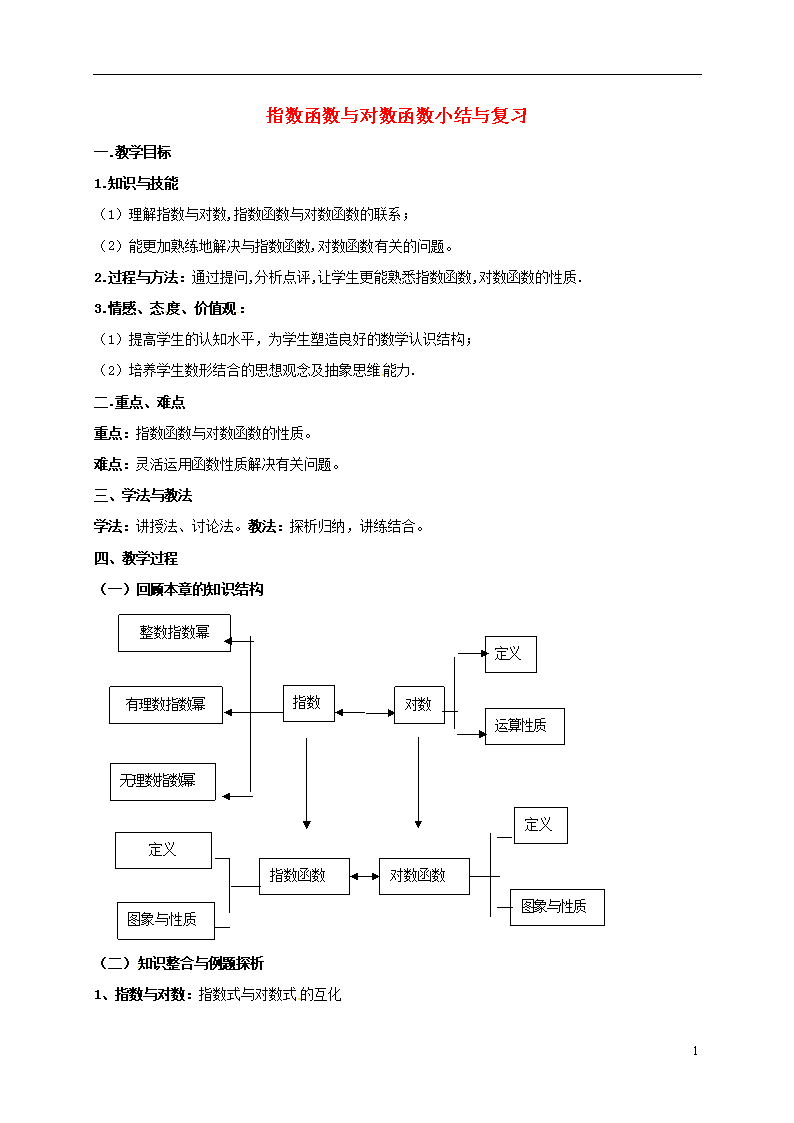
指数函数与对数函数小结与复习 一.教学目标 1.知识与技能 (1)理解指数与对数,指数函数与对数函数的联系; (2)能更加熟练地解决与指数函数,对数函数有关的问题。 2.过程与方法:通过提问,分析点评,让学生更能熟悉指数函数,对数函数的性质. 3.情感、态度、价值观: (1)提高学生的认知水平,为学生塑造良好的数学认识结构; (2)培养学生数形结合的思想观念及抽象思维能力. 二.重点、难点 重点:指数函数与对数函数的性质。 难点:灵活运用函数性质解决有关问题。 三、学法与教法 学法:讲授法、讨论法。教法:探析归纳,讲练结合。 四、教学过程 (一)回顾本章的知识结构 整数指数幂 定义 对数 指数 有理数指数幂 运算性质 无理数指数幂 定义 定义 指数函数 对数函数 图象与性质 图象与性质 (二)知识整合与例题探析 1、指数与对数:指数式与对数式的互化 3 幂值 真数 = N= b 底数 指数←→对数值 提问:在对数式中,a,N,b的取值范围是什么? 例1:已知=,54b=3,用的值 解法1:由=3得=b ∴== 解法2:由 设 所以 即: 所以 因此得: 法1是通过指数化成对数,再由对数的运算性质和换底公式计算结果. 法2是通过对数化成指数,再由指数的运算性质计算出结果,但法2运算的技巧性较大。 2.指数函数与对数函数 问题1:函数分别必须满足什么条件. 问题2:在同一直角坐标系中画出函数的图象,并说明两者之间的关系. 问题3:根据图象说出指数函数与对数函数的性质. 例2:已知函数的图象沿轴方向向左平移1个单位后与的图象关于直线对称,且,则函数的值域为 . 分析:函数关于直线对称的函数为 ∴ 3 ∴ ∵ 小结:底数相同的指数函数与对数函数关于对称,它们之间还有一个关系式子: 例3:已知 (1)求的定义域;(2)求使的的取值范围 分析:(1)要求的定义域, 则应有 (2)注意考虑不等号右边的0化为,则(2)小题变为两种情况分别求出. 建议:通过提问由学生作答 (三)课堂小结: 1.指数与对数实质上只是同一数量关系的两种不同的形式,它们之间可以互化,这种等价互化也是指数运算和对数运算的常用方法. 2.底数相同的指数函数和对数函数互为反函数,它们的图象关于对称,它们在各自的定义域内增减性是一致的,通过函数图象,利用数形结合,记作指数函数与对数函数的性质. (四)布置作业: 1.P90 A组 3 7 2.P91 B组 3 4 五.教后反思 3查看更多