高中数学选修2-2教学课件第四章 章末复习课

高中数学选修2-2教学课件第四章 章末复习课

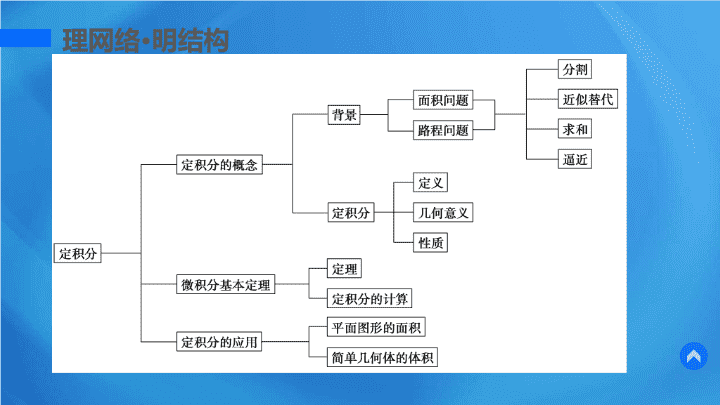
章末复习课 第四章　定积分 内容 索引 01 02 理 网络 明结构 探 题型 提 能力 03 04 理网络 · 明结构 探题型 · 提能力 题型一　定积分的概念及几何 意义 例 1 　根据定积分的几何意义计算定积分 ʃ | x － 2|d x . 解　 根据定积分的几何意义，所求定积分表示的是 y ＝ | x － 2| 和 x ＝ 3 ， x ＝ 1 及 y ＝ 0 所围成的图形的面积，即图中阴影部分面积 . 反思与感悟　 将定积分的求解问题，利用定积分的几何意义转化为求一个图形的面积问题，正确地作出被积函数的图像，然后由求面积的方法求解该定积分是解决本类问题的重点 . 答案　 A 题型二　利用微积分基本定理求定积分 利用微积分基本定理计算定积分与定义法计算定积分相比较，使运算量大大地减少了，因此在计算定积分时要优先考虑微积分基本定理的运用 . 利用微积分基本定理求定积分关键是要找到被积函数的原函数，在找被积函数的原函数时，一定要仔细观察被积函数的结构，结合导数公式和导数的运算性质，才能较快地找到原函数 . 跟踪训练 2 　计算下列定积分： 题型三　定积分的应用 1. 定积分可用来计算曲边梯形的面积，某些曲面面积可以表示成几个曲边梯形面积的和或差的形式 . 2. 利用定积分也可以求出一些简单的几何体体积，如圆锥体、圆柱体、圆台、球体等 . 计算由曲线 y ＝ f ( x ) ，直线 x ＝ a ， x ＝ b 及 x 轴所围成的曲边梯形绕 x 轴旋转一周而生成的旋转体的体积为 V ＝ ʃ π [ f ( x )] 2 d x . 例 3 　 (1) 求由曲线 y ＝ sin x ， y ＝ cos x 及直线 x ＝ 0 ， x ＝ 所 围成图形的面积 . 解　 先画草图如图 . 其次，若选 x 为积分变量，积分下限为 x ＝ 0 ，上限为 x ＝ . 最后， 由图形可知，平面图形由 x ＝ 把 图形分成两块 . (2) 求抛物线 y 2 ＝ 2 px ( p >0) 与直线 x ＝ p 及 x 轴所围成的图形绕 x 轴旋转一周所得旋转体的体积 . 解　 如图所示，因为 y 2 ＝ 2 px ( p >0) ， 所以 跟踪训练 3 　 (1) 求曲线 y ＝ sin x ， x ∈ [0 ， π] 与 x 轴所围成平面图形绕 x 轴旋转一周所得到旋转体的体积 . (2) 如图所示，求由抛物线 y ＝－ x 2 ＋ 4 x － 3 及其在点 A (0 ，－ 3) 和点 B (3 ， 0) 处的切线所围成的图形的面积 . 解　 由题意，知抛物线 y ＝－ x 2 ＋ 4 x － 3 在点 A 处的切线斜率是 k 1 ＝ 4 ，在点 B 处的切线斜率是 k 2 ＝－ 2. 因此，抛物线过点 A 的切线方程为 y ＝ 4 x － 3 ，过点 B 的切线方程为 y ＝－ 2 x ＋ 6. 因此，所求的图形的面积是 更多精彩内容请 登录 http ://www.91taoke.com 谢谢观看