(文理通用)2020届高考数学大二轮复习 第1部分 专题8 选考系列 第2讲 不等式选讲练习
第一部分 专题八 第二讲 不等式选讲
A组
1.已知函数f(x)=|x-2|-|2x-a|,a∈R.
(1)当a=3时,解不等式f(x)>0;
(2)当x∈(-∞,2)时,f(x)<0,求a的取值范围.
[解析] (1)f(x)=
当x>2时,1-x>0,即x<1,此时无解;
当≤x≤2时,5-3x>0,即x<,解得≤x<;
当x<时,x-1>0,即x>1,解得1
恒成立.
∵x∈(-∞,2),∴a-2≥2,∴a≥4.
2.(2018·南宁二模)设实数x,y满足x+=1.
(1)若|7-y|<2x+3,求x的取值范围.
(2)若x>0,y>0,求证:≥xy.
[解析] (1)根据题意,x+=1,
则4x+y=4,即y=4-4x,
则由|7-y|<2x+3,可得|4x+3|<2x+3,
即-(2x+3)<4x+3<2x+3,
解得-10,y>0,
1=x+≥2=,
即≤1,
-xy=(1-),
又由0<≤1,
则-xy=(1-)≥0,
即≥xy.
3.(2018·西安二模)已知函数f(x)=log2(|x+1|+|x-2|-a).
5
(1)当a=7时,求函数f(x)的定义域.
(2)若关于x的不等式f(x)≥3的解集是R,求实数a的最大值.
[解析] (1)由题设知:|x+1|+|x-2|>7;
①当x>2时,得x+1+x-2>7,解得x>4;
②当-1≤x≤2时,得x+1+2-x>7,无解;
③当x<-1时,得-x-1-x+2>7,解得x<-3;
所以函数f(x)的定义域为(-∞,-3)∪(4,+∞).
(2)不等式f(x)≥3,即|x+1|+|x-2|≥a+8;
因为x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3;
又不等式|x+1|+|x-2|≥a+8解集是R;
所以a+8≤3,即a≤-5.
所以a的最大值为-5.
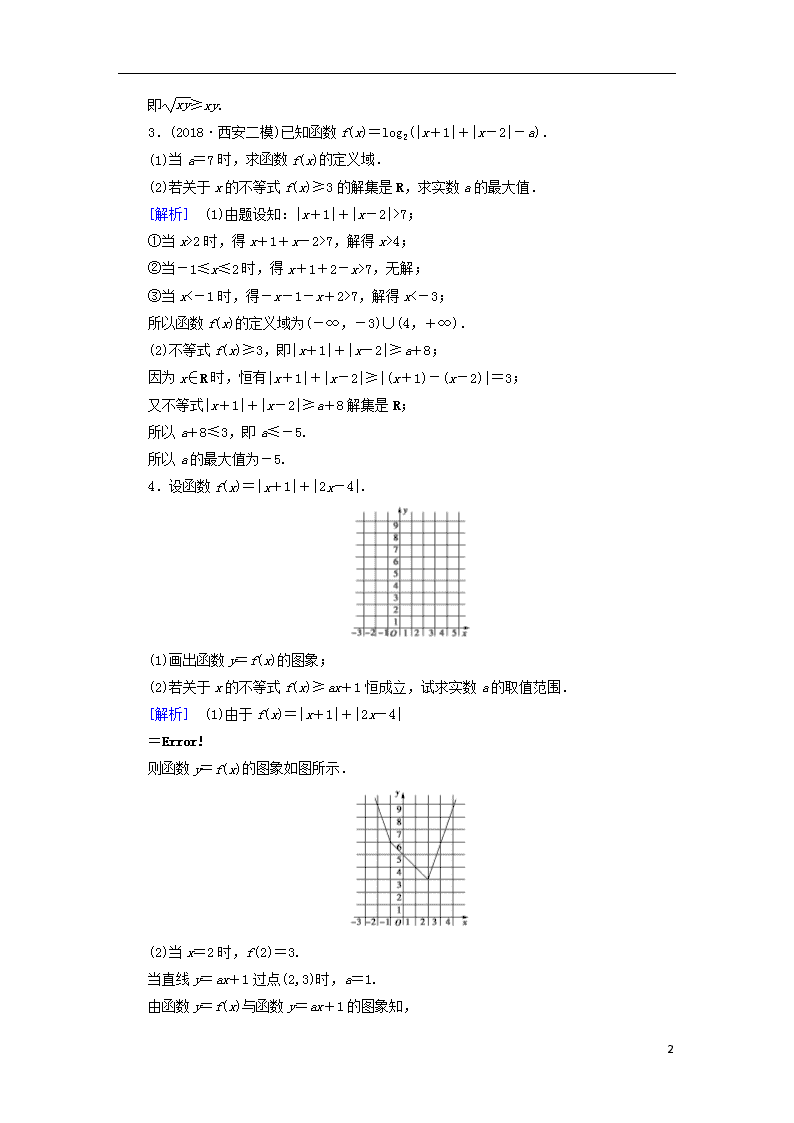
4.设函数f(x)=|x+1|+|2x-4|.
(1)画出函数y=f(x)的图象;
(2)若关于x的不等式f(x)≥ax+1恒成立,试求实数a的取值范围.
[解析] (1)由于f(x)=|x+1|+|2x-4|
=
则函数y=f(x)的图象如图所示.
(2)当x=2时,f(2)=3.
当直线y=ax+1过点(2,3)时,a=1.
由函数y=f(x)与函数y=ax+1的图象知,
当且仅当-3≤a≤1时,函数y=f(x)的图象没有在函数y=ax+1的图象的下方,
因此f(x)≥ax+1恒成立时,a的取值范围为[-3,1].
5
B组
1.设函数f(x)=|2x+1|-|x-3|.
(1)解不等式f(x)>0;
(2)已知关于x的不等式a+30化为
或或
∴x<-4或x>,
即不等式的解集为(-∞,-4)∪(,+∞).
(2)∵f(x)min=-,∴要使a+34;
(2)若∃x∈R,使得不等式|x-3|+|x-a|<4成立,求实数a的取值范围.
[分析] (1)按x=0和3分段讨论或利用绝对值的几何意义求解.
(2)∃x∈R,使不等式f(x)<4成立,即f(x)的最小值小于4.
[解析] (1)由a=0知原不等式为|x-3|+|x|>4
当x≥3时,2x-3>4,解得x>.
当0≤x<3时,3>4,无解.
当x<0时,-2x+3>4,解得x<-.
故解集为{x|x<-或x>}.
(2)由∃x∈R,|x-3|+|x-a|<4成立可得,(|x-3|+|x-a|)min<4.
又|x-3|+|x-a|≥|x-3-(x-a)|=|a-3|,
即(|x-3|+|x-a|)min=|a-3|<4.
解得-1-,所以--2,所以0-1的解集为M.
(1)求M;
(2)已知a∈M,比较a2-a+1与的大小.
[解析] (1)f(x)=|x|-|2x-1|=
由f(x)>-1,得
或或
解得00,
所以a2-a+1>.
5
综上所述:当0.
5