2020八年级数学上册 第11章 数的开方 11

2020八年级数学上册 第11章 数的开方 11

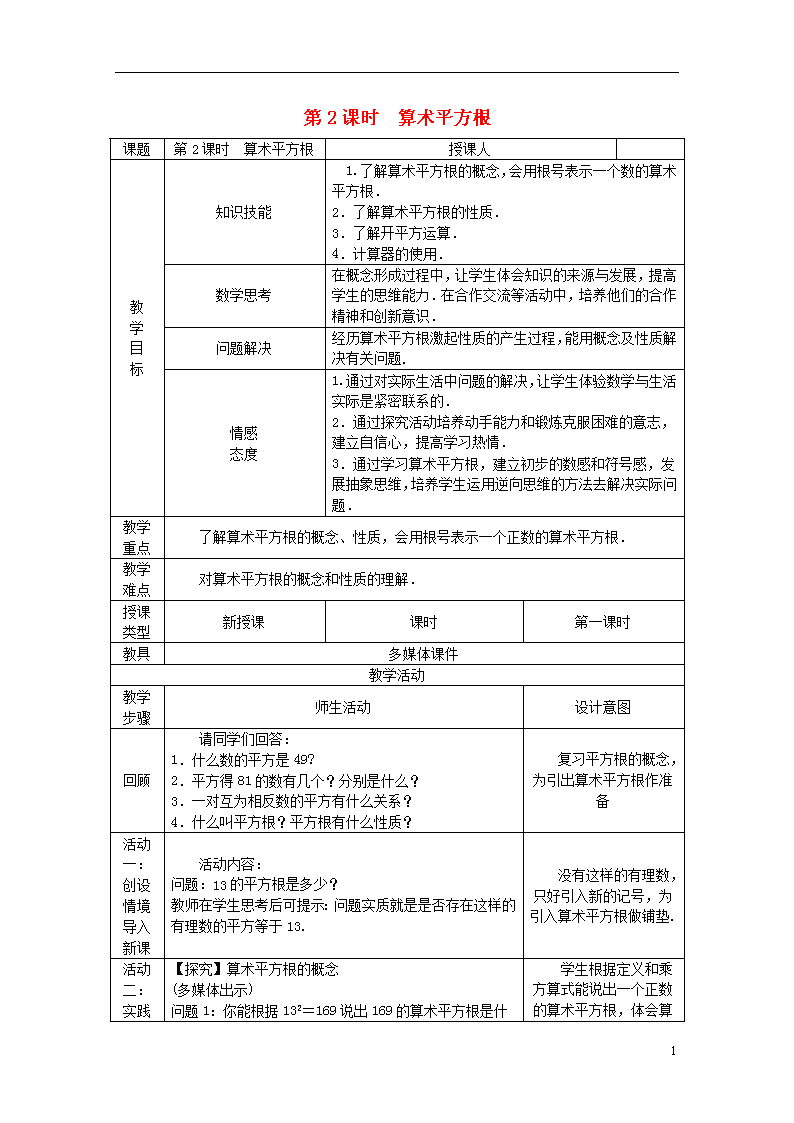
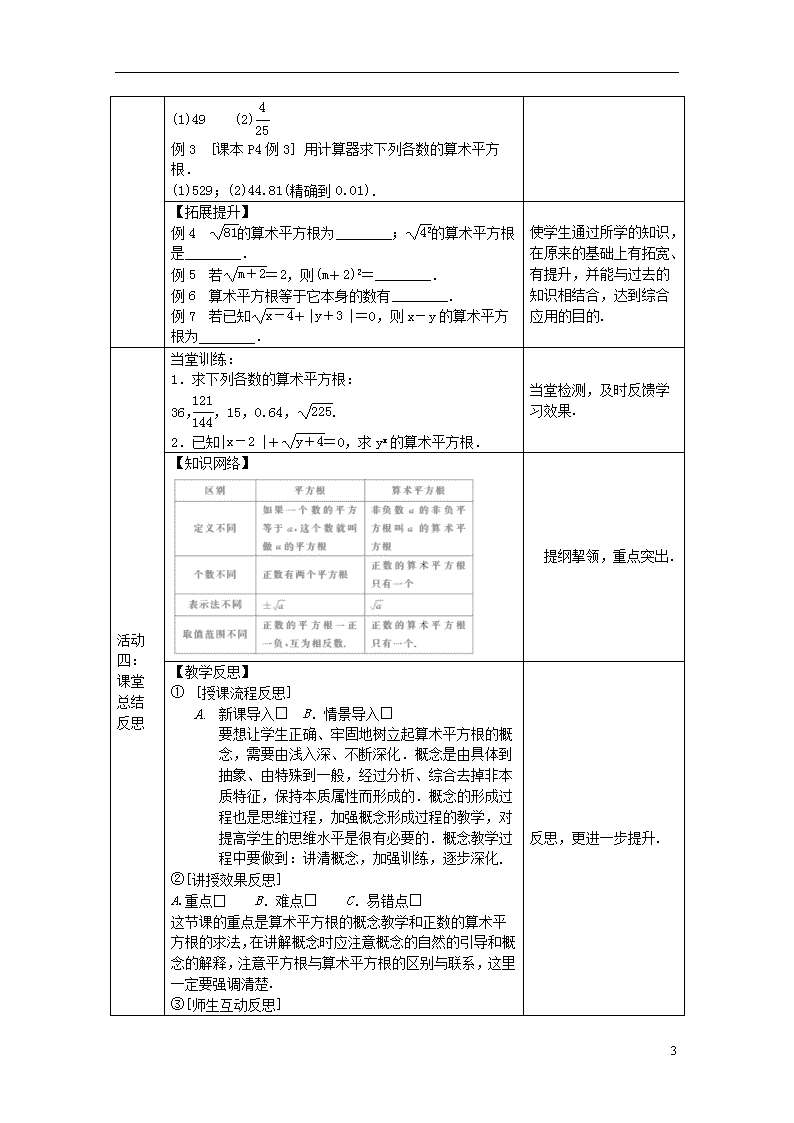
第2课时　算术平方根 课题 第2课时　算术平方根 授课人 教 学 目 标 知识技能 ‎　1.了解算术平方根的概念，会用根号表示一个数的算术平方根．‎ ‎2．了解算术平方根的性质．‎ ‎3．了解开平方运算．‎ ‎4．计算器的使用．‎ 数学思考　‎ 在概念形成过程中，让学生体会知识的来源与发展，提高学生的思维能力．在合作交流等活动中，培养他们的合作精神和创新意识．‎ 问题解决 经历算术平方根激起性质的产生过程，能用概念及性质解决有关问题.‎ 情感 态度 ‎1.通过对实际生活中问题的解决，让学生体验数学与生活实际是紧密联系的．‎ ‎2．通过探究活动培养动手能力和锻炼克服困难的意志，建立自信心，提高学习热情．‎ ‎3．通过学习算术平方根，建立初步的数感和符号感，发展抽象思维，培养学生运用逆向思维的方法去解决实际问题．‎ 教学 重点 ‎　　了解算术平方根的概念、性质，会用根号表示一个正数的算术平方根．‎ 教学 难点 ‎　　对算术平方根的概念和性质的理解．‎ 授课 类型 新授课 课时 第一课时 教具 多媒体课件 教学活动 教学 步骤 师生活动 设计意图 回顾 ‎　　请同学们回答：‎ ‎1．什么数的平方是49?‎ ‎2．平方得81的数有几个？分别是什么？‎ ‎3．一对互为相反数的平方有什么关系？‎ ‎4．什么叫平方根？平方根有什么性质？‎ ‎　　复习平方根的概念，为引出算术平方根作准备 活动 一：‎ 创设 情境 导入 新课 ‎　　活动内容：‎ 问题：13的平方根是多少？‎ 教师在学生思考后可提示：问题实质就是是否存在这样的有理数的平方等于13.‎ ‎　　没有这样的有理数，只好引入新的记号，为引入算术平方根做铺垫.‎ 活动 二：‎ 实践 ‎【探究】算术平方根的概念 ‎(多媒体出示)‎ 问题1：你能根据132‎ ‎　　学生根据定义和乘方算式能说出一个正数的算术平方根，‎ 4‎ 探究 交流 新知 ‎＝169说出169的算术平方根是什么吗？记作什么？‎ 若122＝144，则144的算术平方根是什么呢？记作什么？‎ 问题2：你能根据x2＝7说出7的算术平方根是什么吗？记作什么？在y2＝11中，y所表示的数又是什么吗？‎ 总结：一般地，如果一个正数x的平方等于a，即x2＝a，那么这个正数x就叫做a的算术平方根，记为“”，读作“根号a”．‎ 体会算术平方根的概念，并初步感知平方运算和求正数的算术平方根是互逆的.‎ 活动 三：‎ 开放 训练 体现 应用 ‎【应用举例】‎ 例1　求下列各数的算术平方根：‎ ‎(1)900；(2)1；(3)；(4)14(5)29(6) 解：(1)因为302＝900，所以900的算术平方根是30，即＝30；‎ (1) 因为12＝1，所以1的算术平方根是1，即＝1；‎ ‎　(3)因为()2＝，所以的算术平方根是，即＝；‎ ‎(4)14的算术平方根是.‎ ‎(5)29的算术平方根是.‎ ‎(6)因为10－2＝，()2＝.所以的算术平方根是.‎ 问题：你们现在会求x2＝2，y2＝3，w2＝5中的x，y，z，w的值了吗？‎ 归纳：算术平方根的性质：‎ 一个正数的算术平方根是________数，0的算术平方根是________，________数没有算术平方根．‎ 变式一　求下列各式的值：‎ ，，， 变式二　若一个数的算术平方根是，那么这个数是________．‎ 变式三　(－6)2的算术平方根是(　　)‎ A．－6　　　B．‎36　‎　　C．±6　　　D．6‎ 变式四　如果＝1.5，那么y的值是(　　)‎ A．2.25 B．‎22.5 C．2.55 D．25.5‎ 问题1：负数有平方根吗？‎ 引出开平方的概念：求一个非负数的平方根的运算，叫做开平方．‎ 例2　[课本P3例2] 将下列各数开平方：‎ 体验求一个正数的算术平方根的过程，利用平方运算求一个正数的算术平方根的方法，让学生明白有的正数的算术平方根可以开出来，有的正数的算术平方根只能用根号表示，如14的算术平方根是.‎ 旨在检测学生对算术平方根的概念和性质的掌握情况，以便根据学生情况调整教学进程．练习注意了问题的梯度性，由浅入深，一步步加深对算术平方根的概念以及性质的认识．‎ 让学生知道平方的逆运算是开平方．‎ 例2是由求算术平方根来得到一个数的平方根，是求平方根的另一种方法 例3是了解用计算器求算术平方根.‎ 4‎ ‎(1)49　　(2) 例3　[课本P4例3] 用计算器求下列各数的算术平方根．‎ ‎(1)529；(2)44.81(精确到0.01)．‎ ‎【拓展提升】‎ 例4　的算术平方根为________；的算术平方根是________．‎ 例5　若＝2，则(m＋2)2＝________．‎ 例6　算术平方根等于它本身的数有________．‎ 例7　若已知＋＝0，则x－y的算术平方根为________．‎ 使学生通过所学的知识，在原来的基础上有拓宽、有提升，并能与过去的知识相结合，达到综合应用的目的.‎ 活动 四：‎ 课堂 总结 反思 当堂训练：‎ ‎1．求下列各数的算术平方根：‎ ‎36，，15，0.64，.‎ ‎2．已知＋＝0，求yx的算术平方根．‎ 当堂检测，及时反馈学习效果.‎ ‎【知识网络】‎ ‎　提纲挈领，重点突出.‎ ‎【教学反思】‎ ① ‎[授课流程反思]‎ A. 新课导入□　B．情景导入□‎ 要想让学生正确、牢固地树立起算术平方根的概念，需要由浅入深、不断深化．概念是由具体到抽象、由特殊到一般，经过分析、综合去掉非本质特征，保持本质属性而形成的．概念的形成过程也是思维过程，加强概念形成过程的教学，对提高学生的思维水平是很有必要的．概念教学过程中要做到：讲清概念，加强训练，逐步深化.‎ ‎②[讲授效果反思]‎ A.重点□　　B．难点□　　C．易错点□‎ 这节课的重点是算术平方根的概念教学和正数的算术平方根的求法，在讲解概念时应注意概念的自然的引导和概念的解释，注意平方根与算术平方根的区别与联系，这里一定要强调清楚.‎ ‎③[师生互动反思]‎ 反思，更进一步提升.‎ 4‎ 通过师生间频繁的互动，使学生深刻理解概念，准确表述，并通过练习巩固掌握.‎ ‎④[习题反思]‎ 好题题号__________________________________________‎ 错题题号__________________________________________‎ 4‎