- 2021-06-02 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
汉中市2020届高三年级教学质量第二次检测考试文科数学
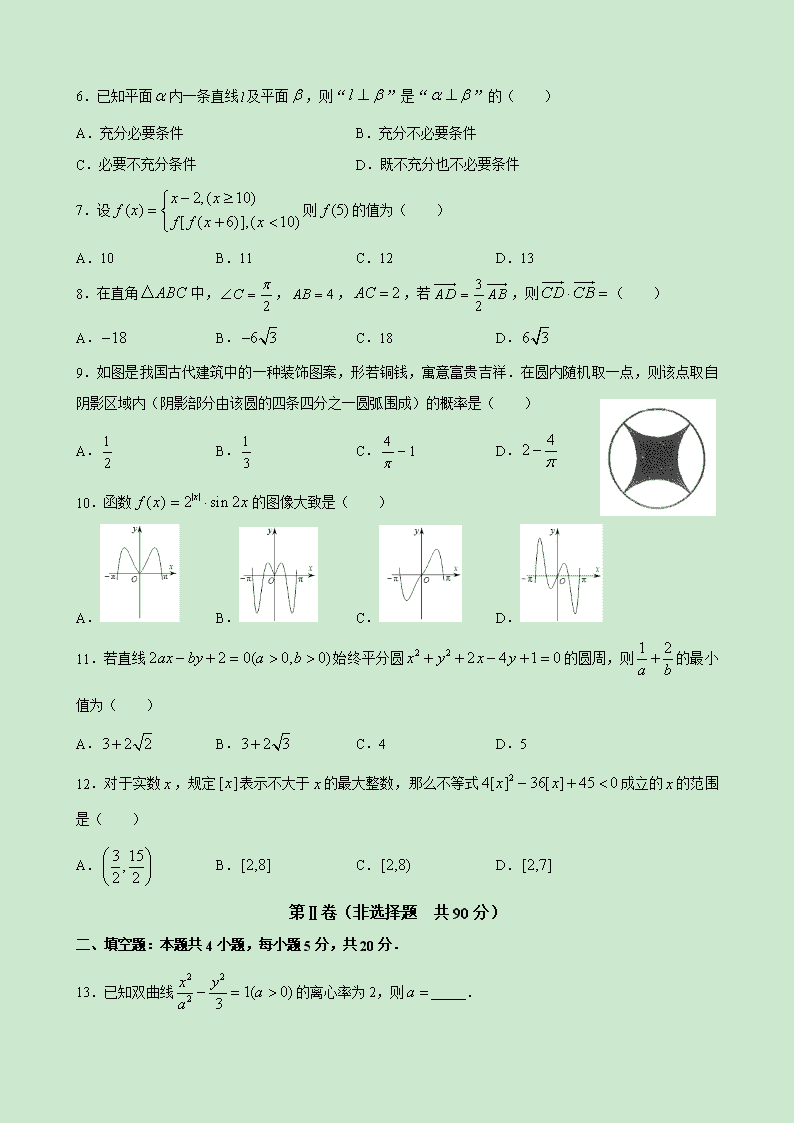
汉中市 2020 届高三年级教学质量第二次检测考试文科数学 本试卷共 23 题,共 150 分,共 4 页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域 内. 2.选择题必须使用 2B 铅笔填涂;非选择题必须用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清 楚. 3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷 上答题无效. 4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑. 5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀. 第Ⅰ卷(选择题 共 60 分) 一、选择题:本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目 要求的. 1.若集合 , ,全集 ,则集合 中的元素共有( ) A.3 个 B.4 个 C.5 个 D.6 个 2.在复平面内,复数 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.若 ,则下列不等式中不成立的是( ) A. B. C. D. 4.总体由编号为 01,02,…19,20 的 20 个个体组成.利用下面的随机数表选取 5 个个体,选取方法是 从随机数表第 1 行的第 5 列和第 6 列数字开始由左到右依次选取两个数字,则选出来的第 5 个个体的编号 为( ) 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4935 8200 3623 4869 6938 7481 A.01 B.02 C.07 D.08 5.已知函数 ,则下列判断错误的是( ) A. 的最小正周期为 B. 的值域为 C. 的图象关于直线 对称 D. 的图象关于点 对称 {4,5,7,9}M = {3,4,7,8,9}N = U M N= ∪ ( )U M N∩ 2 1 (1 ) i i + − 0a b< < | | | |a b> 2 2a b> 1 1 a b > 1 1 a b a >− ( ) cos2 3sin2 1f x x x= + + ( )f x π ( )f x [ 1,3]− ( )f x 6x π= ( )f x ,04 π − 6.已知平面 内一条直线 及平面 ,则“ ”是“ ”的( ) A.充分必要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 7.设 则 的值为( ) A.10 B.11 C.12 D.13 8.在直角 中, , , ,若 ,则 ( ) A. B. C.18 D. 9.如图是我国古代建筑中的一种装饰图案,形若铜钱,寓意富贵吉祥.在圆内随机取一点,则该点取自 阴影区域内(阴影部分由该圆的四条四分之一圆弧围成)的概率是( ) A. B. C. D. 10.函数 的图像大致是( ) A. B. C. D. 11.若直线 始终平分圆 的圆周,则 的最小 值为( ) A. B. C.4 D.5 12.对于实数 ,规定 表示不大于 的最大整数,那么不等式 成立的 的范围 是( ) A. B. C. D. 第Ⅱ卷(非选择题 共 90 分) 二、填空题:本题共 4 小题,每小题 5 分,共 20 分. 13.已知双曲线 的离心率为 2,则 _____. α l β l β⊥ α β⊥ 2,( 10)( ) [ ( 6)],( 10) x xf x f f x x − ≥= + < (5)f ABC△ 2C π∠ = 4AB = 2AC = 3 2AD AB= CD CB⋅ = 18− 6 3− 6 3 1 2 1 3 4 1π − 42 π− | |( ) 2 sin2xf x x= ⋅ 2 2 0( 0, 0)ax by a b− + = > > 2 2 2 4 1 0x y x y+ + − + = 1 2 a b + 3 2 2+ 3 2 3+ x [ ]x x 24[ ] 36[ ] 45 0x x− + < x 3 15,2 2 [2,8] [2,8) [2,7] 2 2 2 1( 0)3 x y aa − = > a = 14.在 中,内角 的对边分别是 ,若 , ,则 ____. 15.三棱锥 中, 底面 , ,底面 中 ,边 ,则 三棱锥 外接球的体积等于______. 16.已知函数 在 上单调递增,则实数 的取值范围是______. 三、解答题:共 70 分,解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,每个试题考 生都必须作答.第 22、23 题为选考题,考生根据要求作答. (一)必考题:共 60 分 17.设等差数列 满足 , . (Ⅰ)求数列 的通项公式; (Ⅱ)求 的前 项和 及使得 最小的 的值. 18 . 如 图 , 四 棱 锥 中 , 底 面 , , 点 在 线 段 上 , 且 . (Ⅰ)求证: 平面 ; (Ⅱ)若 , , , , 求四棱锥 的正弦值. 19.眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉, 改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果, 在应届高三的全体 800 名学生中随机抽取了 100 名学生进行视力检查,并得到如图的频率分布直方图. (1)若直方图中后三组的频数成等差数列,试估计全年级视力在 5.0 以上的人数; (2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了 调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过 0.005 的前提下认为视力与眼保健操 有关系? 是否做操 是否近视 不做操 做操 ABC△ , ,A B C , ,a b c 2 2 3a b bc− = sin 2 3sinC B= A = P ABC− PA ⊥ ABC 2 2PA = ABC△ 4BAC π∠ = 2BC = P ABC− 2( ) lnf x ax x x= − 1 ,e +∞ a { }na 3 9a = − 10 5a = { }na { }na n nS nS n P ABCD− PA ⊥ ABCD AB AD⊥ E AD CE AB CE ⊥ PAD 1PA AB= = 3AD = 2CD = 45CDA∠ = ° P ABCD− 附: 0.10 0.05 0.025 0.010 0.005 2.706 3.841 5.024 6.635 7.879 20.如图,椭圆 的长轴长为 4,点 为椭圆上的三个点, 为椭圆的右端点, 过中心 ,且 , . (1)求椭圆的标准方程; (2)设 是椭圆上位于直线 同侧的两个动点(异于 ),且满足 ,试讨论直线 与直线 斜率之间的关系,并求证直线 的斜率为定值. 21.已知函数 ,且其导函数 的图像过原点. (1)若存在 ,使得 ,求 的最大值; (2)当 时,求函数 的零点个数. (二)选考题:共 10 分.请考生在 22、23 题任选一题作答.如果多做,则按所做的第一题计分. 22.[选修 4-4:坐标系与参数方程] 已知曲线 的极坐标方程为 ,直线 的参数方程为 ( 为参数). (1)求曲线 的直角坐标方程与直线 的普通方程; (2)已知点 ,直线 与曲线 交于 两点,求 . 23.[选修 4-5:不等式选讲] 已知函数 近视 44 32 不近视 6 18 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + ( )2P k k≥ k 2 2 2 2 1( 0)x y a ba b + = > > , ,A B C A BC O | | 2 | |BC AB= 3ABCS =△ ,P Q AC ,A C PBC QBA∠ = ∠ BP BQ PQ 3 21 1( ) ( , )3 2 af x x x bx a a b += − + + ∈R ( )f x′ 0x < ( ) 9f x′ = − a 0a > ( )f x C 4cosρ θ= l 31 2 1 2 x t y t = + = t C l (1,0)M l C A B、 | |MA MB−‖ ‖ ( ) |2 |f x x a a= − + (1)当 时,求不等式 的解集; (2)设函数 .当 时, ,求 的取值范围. 汉中市 2020 届高三年级教学质量第二次检测考试 文科数学参考答案 一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B D A D B B C C D A C 二、填空题 13.1 14. 15. 16. 三、解答题 17 解:(1)设等差数列 的公差为 ,由 及 , 得 解得 数列 的通项公式为 (2)由(1)知 因为 所以 时, 取得最小值. 2a = ( ) 6f x ≤ ( ) | 2 1|g x x= − x R∈ ( ) ( ) 3f x g x+ ≥ a 6 π 32 3 π 1 ,2 +∞ { }na d 1 ( 1)na a n d= + − 3 9a = − 10 5a = 1 1 2 9 9 5 a d a d + = − + = 1 13 2 a d = − = { }na 2 15na n= − 2 14nS n n= − 2( 7) 49nS n= − − 7n = nS 18 解:(1)证明 因为 平面 , 平面 , 所以 . 因为 , ,所以 . 又 ,所以 平面 . (2)解:由(1)可知 在 中, , 所以 . 又因为 , ,所以四边形 为矩形. 所以 又 平面 , , 19.解:(1)由图可知,第一组有 3 人,第二组 7 人,第三组 27 人, 因为后三组的频数成等差数列,共有 (人) 所以后三组频数依次为 24,21,18, 所以视力在 5.0 以上的频率为 0.18, 故全年级视力在 5.0 以上的人数约为 人 PA ⊥ ABCD CE ⊂ ABCD PA CE⊥ AB AD⊥ CE AB CE AD⊥ PA AD A∩ = CE ⊥ PAD CE AD⊥ Rt CDE△ cos45 1DE CD= ⋅ ° = sin45 1CE CD= ⋅ ° = 2AE AD ED= − = 1AB CE= = CE AB ABCE 1 2ECDABCEABCDS S S AB AE CE DE= + = ⋅ + ⋅△矩形四变形 1 51 2 1 12 2 = × + × × = PA ⊥ ABCD 1PA = 1 1 5 513 3 2 6ABCDP ABCDV S PA− = ⋅ = × × =四边形四棱锥 100 (3 7 27) 63− + + = 800 0.18 144× = (2) 因此能在犯错误的概率不超过 0.005 的前提下认为视力与眼保健操有关系. 21.解: , 由 得 , . (1)存在 ,使得 , , , 当且仅当 时, . 所以 的最大值为 . (2)当 时, 0 + 0 - 0 + 极大值 极小值 , , 的变化情况如上表: 的极大值 , 的极小值 2 2 100 (44 18 32 6) 50 50 76 24k × × − ×= × × × 150 7.895 7.87919 = ≈ > 3 21 1( ) 3 2 af x x x bx a += − + + 2( ) ( 1)f x x a x b′ = − + + (0) 0f ′ = 0b = ( ) ( 1)f x x x a′ = − − 0x < ( ) ( 1) 9f x x x a′ = − − = − 9 9 91 ( ) 2 ( ) 6a x x xx x x − − = − − = − + − ≥ − ⋅ − = 7a ≤ − 3x = − 7a = − a 7− 1a > x ( ,0)−∞ ( , 1)a−∞ + 1a + ( 1, )a + +∞ ( )f x′ ( )f x ↑ ↓ ↑ x ( )f x′ ( )f x ( )f x (0) 0f a= > ( )f x 2 3 31 1 1 1( 1) ( 1) 3 06 6 2 4f a a a a a + = − + = − + − + < 又 , , . 所以函数 在区间 , , 内各有一个零点, 故函数 共有三个零点. 22.解:(1)对于曲线 的极坐标方程为 ,可得 , 又由 ,可得 ,即 , 所以曲线 的直角坐标方程为 . 由直线 的参数方程为 ( 为参数),消去参数可得, 直线 的普通方程为 ,即 . (2)设 两点对应的参数分别为 ,将直线 的参数方程 ( 为参数)代入曲线 中, 可得 . 化简得 , 14( 2) 03f a− = − − < 21 3( ) ( 1)3 2f x x x a a = − + + 3 ( 1) 02f a a + = > ( )f x ( 2,0)− (0, 1)a + 31, ( 1)2a a + + ( )f x C 4cosρ θ= 2 4 cosρ ρ θ= cos sin x y ρ θ ρ θ = = 2 2 4x y x+ = 2 2( 2) 4x y− + = C 2 2( 2) 4x y− + = l 31 2 1 2 x t y t = + = t l 3 ( 1)3y x= − 3 3 3 3y x= − ,A B 1 2,t t l 31 2 1 2 x t y t = + = t 2 2: 4 0C x y x+ − = 2 23 1 31 4 1 02 4 2t t t + + − + = 2 3 3 0t t− − = 设点 所对应的参数分别是 故 , . 所以 . 23.解:(1)当 时, . 解不等式 得 . 因此 的解集为 . (Ⅱ)当 时, , 所以当 时, 等价于 .① 当 时,①等价于 ,无解. 当 时,①等价于 ,解得 . 所以 的取值范围是 . ,A B 1 2,t t 1 2 3t t+ = 1 2 3t t⋅ = − 1 2 1 2| | || || | | || 3MA MB t t t t− = − = + =‖ 2a = ( ) | 2 2 | 2f x x= − + | 2 2 | 2 6x − + 1 3x− ( ) 6f x { | 1 3}x x− x R∈ ( ) ( ) | 2 | |1 2 | | 2 1 2 | |1 |f x g x x a a x x a x a a a+ = − + + − − + − + = − + x R∈ ( ) ( ) 3f x g x+ |1 | 3a a− + ≥ 1a 1 3a a− + 1a > 1 3a a− + 2a a [2, )+∞查看更多