- 2021-06-02 发布 |
- 37.5 KB |
- 2页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019七年级数学上册 第六章 平面图形的认识(一)期末练习2(无答案)(新版)苏科版
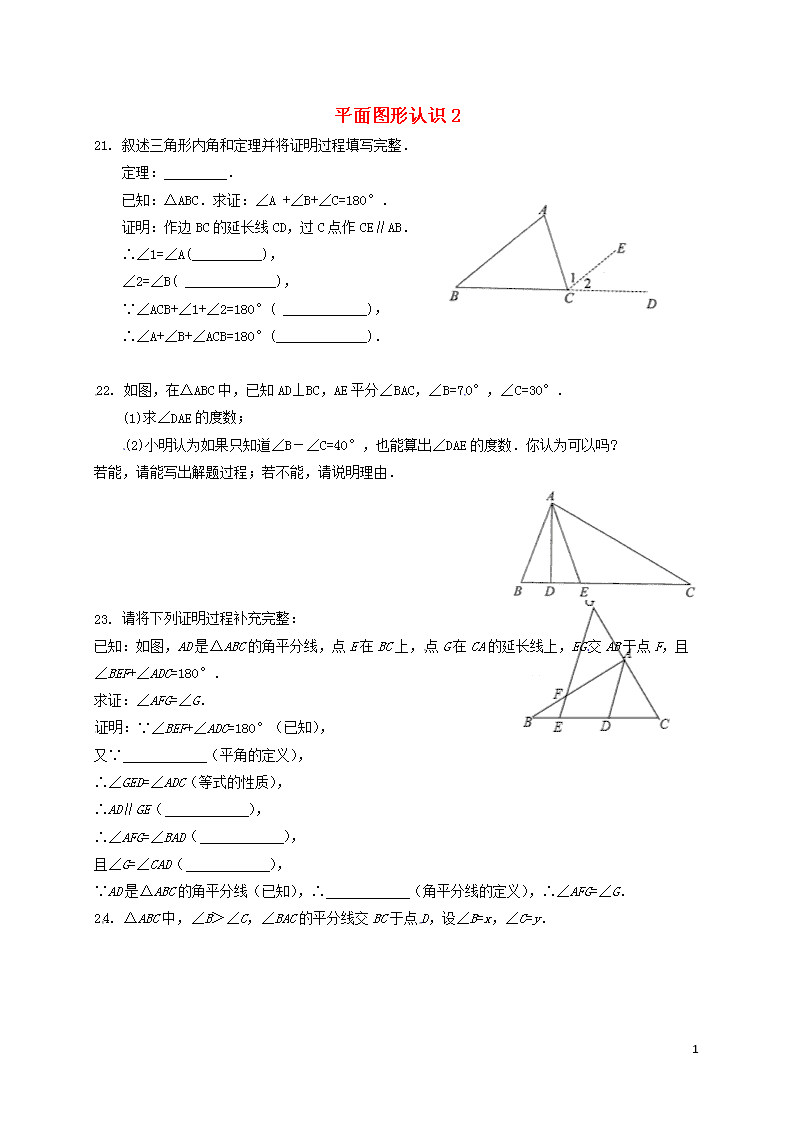
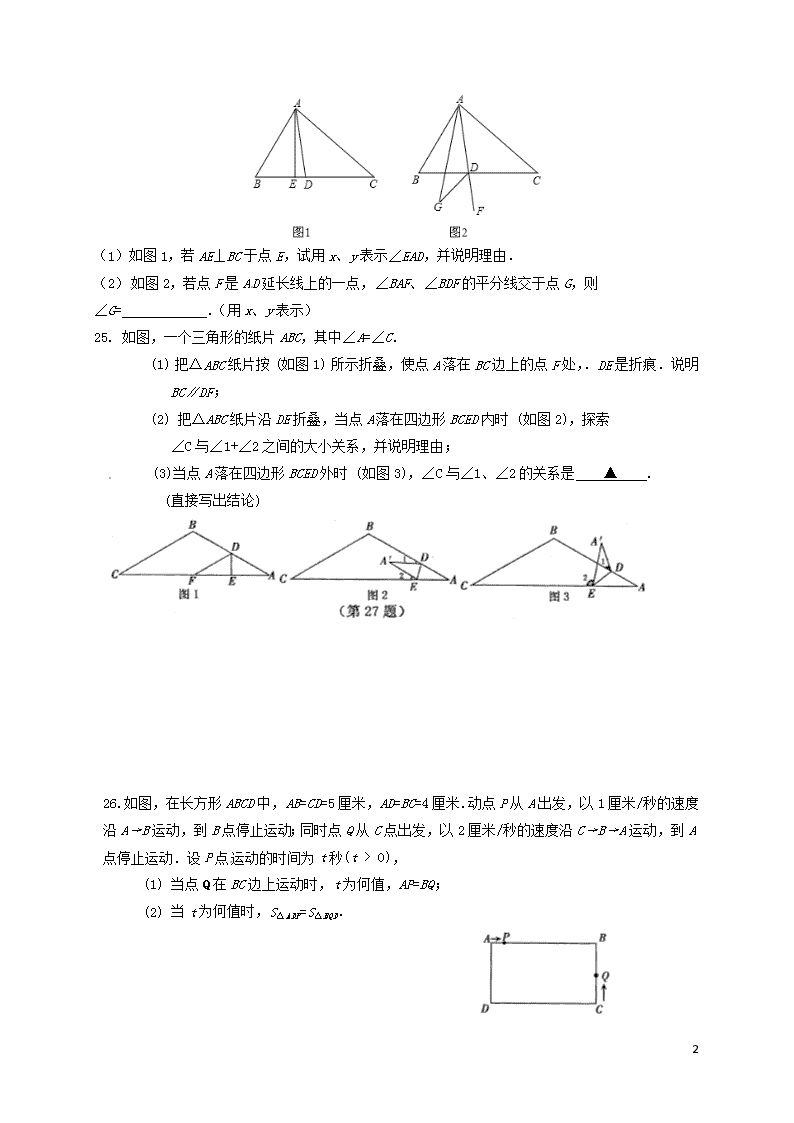
平面图形认识2 21. 叙述三角形内角和定理并将证明过程填写完整. 定理:_________. 已知:△ABC.求证:∠A +∠B+∠C=180°. 证明:作边BC的延长线CD,过C点作CE∥AB. ∴∠1=∠A(__________), ∠2=∠B( _____________), ∵∠ACB+∠1+∠2=180°( ____________), ∴∠A+∠B+∠ACB=180°(_____________). 22. 如图,在△ABC中,已知AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. (1)求∠DAE的度数; (2)小明认为如果只知道∠B-∠C=40°,也能算出∠DAE的度数.你认为可以吗? 若能,请能写出解题过程;若不能,请说明理由. 23. 请将下列证明过程补充完整: 已知:如图,AD是△ABC的角平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠BEF+∠ADC=180°. 求证:∠AFG=∠G. 证明:∵∠BEF+∠ADC=180°(已知), 又∵ (平角的定义), ∴∠GED=∠ADC(等式的性质), ∴AD∥GE( ), ∴∠AFG=∠BAD( ), 且∠G=∠CAD( ), ∵AD是△ABC的角平分线(已知),∴ (角平分线的定义),∴∠AFG=∠G. 24. △ABC中,∠B>∠C,∠BAC的平分线交BC于点D,设∠B=x,∠C=y. 2 (1)如图1,若AE⊥BC于点E,试用x、y表示∠EAD,并说明理由. (2)如图2,若点F是AD延长线上的一点,∠BAF、∠BDF的平分线交于点G,则∠G= .(用x、y表示) 25. 如图,一个三角形的纸片ABC,其中∠A=∠C. (1) 把△ABC纸片按 (如图1) 所示折叠,使点A落在BC边上的点F处,.DE是折痕.说明 BC∥DF; (2) 把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索 ∠C与∠1+∠2之间的大小关系,并说明理由; (3)当点A落在四边形BCED外时 (如图3),∠C与∠1、∠2的关系是 ▲ . (直接写出结论) 26. 如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米. 动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t > 0), (1) 当点Q在BC边上运动时,t为何值,AP=BQ; (2) 当t为何值时,S△ADP=S△BQD. 2查看更多