- 2021-06-01 发布 |
- 37.5 KB |
- 3页

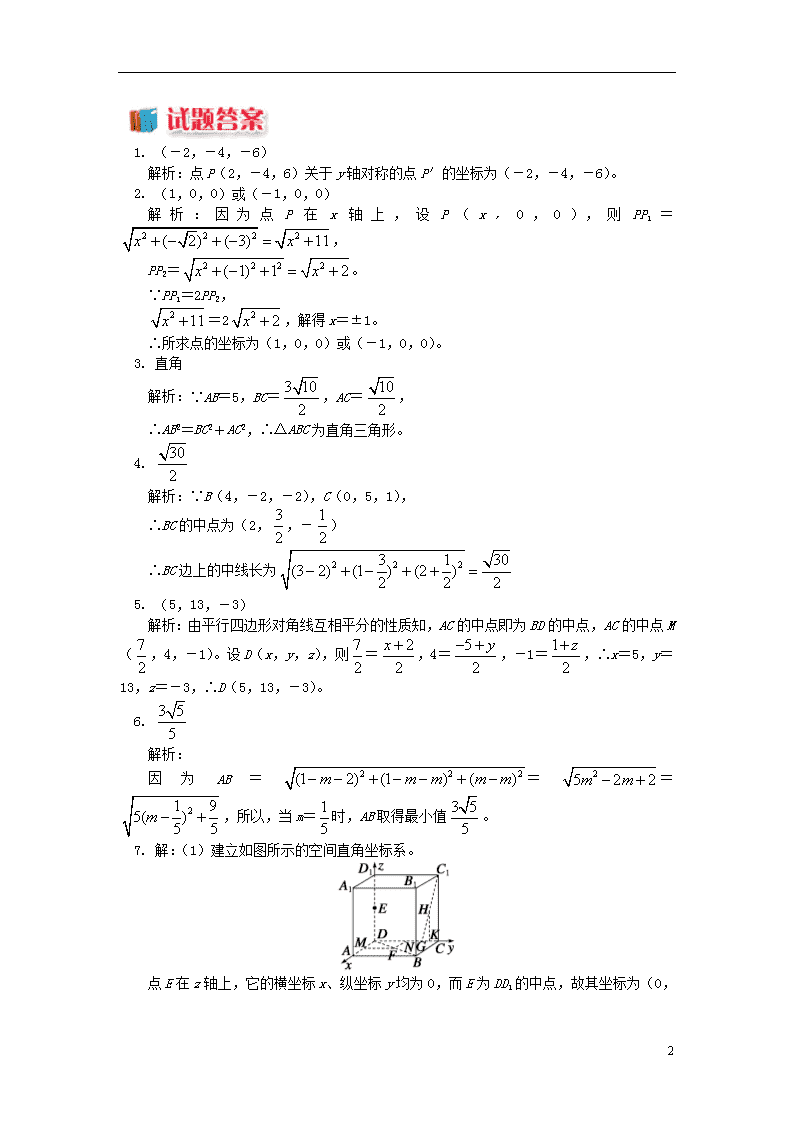
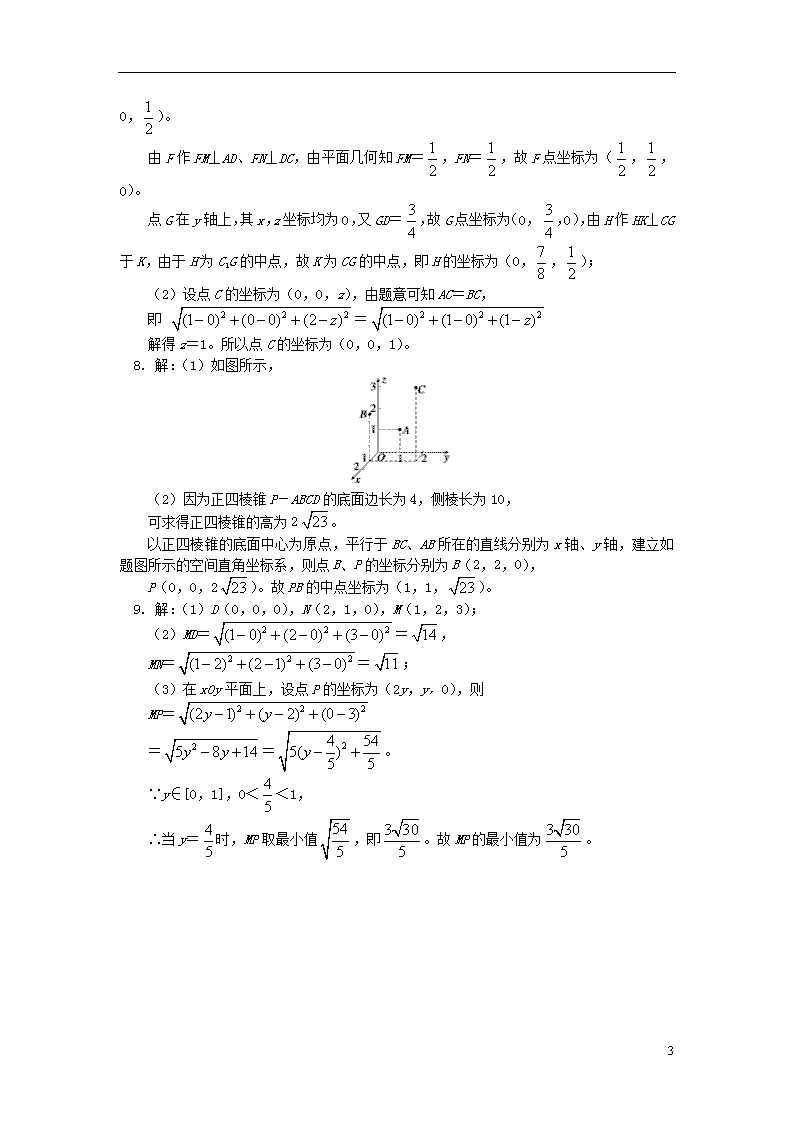
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第2章 平面解析几何初步 第三节 空间直角坐标系2 空间两点间距离习题 苏教版
空间两点间距离 (答题时间:40分钟) 1. (南京检测)在空间直角坐标系中,点P(2,-4,6)关于y轴对称的点P′的坐标为____________。 2. 点P在x轴上,它到点P1(0,,3)的距离是到点P2(0,1,-1)的距离的2倍,则点P的坐标是________。 3. 已知△ABC顶点坐标分别为A(-1,2,3)、B(2,-2,3)、C(,,3),则△ABC为________三角形。 4. (福建八县联考)已知△ABC三个顶点的坐标分别为A(3,1,2)、B(4,-2,-2)、C(0,5,1),则BC边上的中线长________。 5. 已知平行四边形ABCD,且A(4,1,3)、B(2,-5,1)、C(3,7,-5),则顶点D的坐标为__________。 **6. 已知点A(2,m,m),B(1-m,1-m,m),则AB的最小值为________。 **7.(1)在棱长为1的正方体ABCD—A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=CD,H为C1G的中点,试建立适当的坐标系,写出E、F、G、H的坐标。 (2)(辽宁实验中学检测)在空间直角坐标系中,在z轴上求一点C,使得点C到点A(1,0,2)与点B(1,1,1)的距离相等。 *8.(1)在空间直角坐标系中画出下列各点(不写画法,保留作图痕迹):A(0,1,1),B(1,0,2),C(1,2,3); (2)已知正四棱锥P-ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出PB中点的坐标。 ***9. 长方体ABCD-A1B1C1D1中,AB=BC=2,D1D=3,点M是B1C1的中点,点N是AB的中点。建立如图所示空间直角坐标系。 (1)写出点D、N、M的坐标; (2)求线段MD、MN的长度; (3)设点P是线段DN上的动点,求MP的最小值。 3 1. (-2,-4,-6) 解析:点P(2,-4,6)关于y轴对称的点P′的坐标为(-2,-4,-6)。 2. (1,0,0)或(-1,0,0) 解析:因为点P在x轴上,设P(x,0,0),则PP1=, PP2=。 ∵PP1=2PP2, =2,解得x=±1。 ∴所求点的坐标为(1,0,0)或(-1,0,0)。 3. 直角 解析:∵AB=5,BC=,AC=, ∴AB2=BC2+AC2,∴△ABC为直角三角形。 4. 解析:∵B(4,-2,-2),C(0,5,1), ∴BC的中点为(2,,-) ∴BC边上的中线长为 5. (5,13,-3) 解析:由平行四边形对角线互相平分的性质知,AC的中点即为BD的中点,AC的中点M(,4,-1)。设D(x,y,z),则=,4=,-1=,∴x=5,y=13,z=-3,∴D(5,13,-3)。 6. 解析: 因为AB===,所以,当m=时,AB取得最小值。 7. 解:(1)建立如图所示的空间直角坐标系。 点E在z轴上,它的横坐标x、纵坐标y均为0,而E为DD1 3 的中点,故其坐标为(0,0,)。 由F作FM⊥AD、FN⊥DC,由平面几何知FM=,FN=,故F点坐标为(,,0)。 点G在y轴上,其x,z坐标均为0,又GD=,故G点坐标为(0,,0),由H作HK⊥CG于K,由于H为C1G的中点,故K为CG的中点,即H的坐标为(0,,); (2)设点C的坐标为(0,0,z),由题意可知AC=BC, 即 = 解得z=1。所以点C的坐标为(0,0,1)。 8. 解:(1)如图所示, (2)因为正四棱锥P-ABCD的底面边长为4,侧棱长为10, 可求得正四棱锥的高为2。 以正四棱锥的底面中心为原点,平行于BC、AB所在的直线分别为x轴、y轴,建立如题图所示的空间直角坐标系,则点B、P的坐标分别为B(2,2,0), P(0,0,2)。故PB的中点坐标为(1,1,)。 9. 解:(1)D(0,0,0),N(2,1,0),M(1,2,3); (2)MD==, MN==; (3)在xOy平面上,设点P的坐标为(2y,y,0),则 MP= ==。 ∵y∈[0,1],0<<1, ∴当y=时,MP取最小值,即。故MP的最小值为。 3查看更多